Leaf Angle Distribution

% Supplemental program 2.2

% ------------------------------------------------------------------------------
% Evaluate the leaf angle probability density function (PDF) from the beta
% distribution using the mean and standard deviation of the leaf inclination 
% angle. The leaf angle PDF is calculated for 9 angle classes between 5 and 85 
% degrees in increments of 10 degrees.
% ------------------------------------------------------------------------------

% --- The variable "leaf" defines the leaf angle distribution type with parameters:
% lad_ave - mean leaf angle (radians)
% lad_std - standard deviation of leaf angle (radians)

  leaf = 'Planophile';
% leaf = 'Erectophile';
% leaf = 'Plagiophile';
% leaf = 'Uniform';
% leaf = 'Spherical';

switch leaf
   case 'Planophile'
   lad_ave = 26.76 * (pi/180);
   lad_std = 18.5068 * (pi/180);
   case 'Erectophile'
   lad_ave = 63.24 * (pi/180);
   lad_std = 18.4960 * (pi/180);
   case 'Plagiophile'
   lad_ave = 45.00 * (pi/180);
   lad_std = 16.2681 * (pi/180);
   case 'Uniform'
   lad_ave = 45.00 * (pi/180);
   lad_std = 25.9808 * (pi/180);
   case 'Spherical'
   lad_ave = 57.30 * (pi/180);
   lad_std = 21.5485 * (pi/180);
end

% --- Convert these to the p,q parameters for the beta distribution

num = 1 - (lad_std*lad_std + lad_ave*lad_ave) / (lad_ave * pi / 2);
den = (lad_std*lad_std + lad_ave*lad_ave) / (lad_ave*lad_ave) - 1;
p = num / den;
q = ((pi/2) / lad_ave - 1) * p;

% --- Calculate leaf inclination angle probability density function (PDF) and
% fractional abundance (lad) for 9 10-degree bins 

dangle = 10 * (pi/180);                      % Leaf inclination angle increment (radians)
angle = [5, 15, 25, 35, 45, 55, 65, 75, 85]; % Leaf inclination angle (degrees)
angle = angle * (pi/180);                    % degrees -> radians

% --- Loop through each angle

for i = 1:length(angle)
   x = angle(i) / (pi/2);
   fp = x ^ (p - 1);
   fq = (1 - x) ^ (q - 1);
   beta_pdf(i) = 2 / pi * fp * fq / beta(p,q);   % Leaf angle probability density function 
   beta_lad(i) = beta_pdf(i) * dangle;           % Fraction of leaves in this angle bin
end

% --- Calculate the known solution

for i = 1:length(angle)

   % Exact leaf angle probability density function

   switch leaf
      case 'Planophile'
      exact_pdf(i) = 2 / pi * (1 + cos(2 * angle(i)));
      case 'Erectophile'
      exact_pdf(i) = 2 / pi * (1 - cos(2 * angle(i)));
      case 'Plagiophile'
      exact_pdf(i) = 2 / pi * (1 - cos(4 * angle(i)));
      case 'Uniform'
      exact_pdf(i) = 2 / pi;
      case 'Spherical'
      exact_pdf(i) = sin(angle(i));
   end

   % Exact relative leaf angle distribution (fraction)

   exact_lad(i) = exact_pdf(i) * dangle;

end

% --- Print out fractional abundance and compare with known solution
% sum -  sum of PDF * dangle (this sums to 1)
% ave -  sum of angle * PDF * dangle (this is the mean)

beta_sum = 0;
beta_ave = 0;
exact_sum = 0;
exact_ave = 0;

fprintf(' \n')
fprintf('Leaf type = %15s\n', leaf)
fprintf('     Angle         beta            exact \n')
for i = 1:length(angle)
   beta_sum = beta_sum + beta_lad(i);
   beta_ave = beta_ave + angle(i) * beta_lad(i);
   exact_sum = exact_sum + exact_lad(i);
   exact_ave = exact_ave + angle(i) * exact_lad(i);
   fprintf('%10.2f %15.4f %15.4f \n', angle(i)*180/pi, beta_lad(i), exact_lad(i))
end

fprintf(' \n')
fprintf('beta distribution \n')
fprintf('Sum of leaf angle distribution = %15.4f\n', beta_sum)
fprintf('Mean leaf angle = %15.4f\n', beta_ave*180/pi)
fprintf(' \n')
fprintf('Exact solution \n')
fprintf('Sum of leaf angle distribution = %15.4f\n', exact_sum)
fprintf('Mean leaf angle = %15.4f\n', exact_ave*180/pi)

% --- Analytical mean leaf angle

switch leaf
   case 'Planophile'
   fx = @(x) x .* 2 / pi .* (1 + cos(2 .* x));
   case 'Erectophile'
   fx = @(x) x .* 2 / pi .* (1 - cos(2 .* x));
   case 'Plagiophile'
   fx = @(x) x .* 2 / pi .* (1 - cos(4 .* x));
   case 'Uniform'
   fx = @(x) x .* 2 / pi;
   case 'Spherical'
   fx = @(x) x .* sin(x);
end
analytical_ave = integral(fx, 0, pi/2);

fprintf(' \n')
fprintf('Analytical solution \n')
fprintf('Mean leaf angle = %15.4f\n', analytical_ave*180/pi)

% --- Calculate Ross index 

F1 = beta_lad(1) + beta_lad(2) + beta_lad(3);
F2 = beta_lad(4) + beta_lad(5) + beta_lad(6);
F3 = beta_lad(7) + beta_lad(8) + beta_lad(9);
beta_xl = 0.5 * (abs(0.134-F1) + abs(0.366-F2) + abs(0.5-F3));
if ((0.5-F3) < 0) 
   beta_xl = -beta_xl;
end

F1 = exact_lad(1) + exact_lad(2) + exact_lad(3);
F2 = exact_lad(4) + exact_lad(5) + exact_lad(6);
F3 = exact_lad(7) + exact_lad(8) + exact_lad(9);
exact_xl = 0.5 * (abs(0.134-F1) + abs(0.366-F2) + abs(0.5-F3));
if ((0.5-F3) < 0) 
   exact_xl = -exact_xl;
end

fprintf(' \n')
fprintf('Ross index \n')
fprintf('beta distribution = %15.4f\n', beta_xl)
fprintf('   Exact solution = %15.4f\n', exact_xl)

% --- Graph PDFs

x = 0:(pi/2)/100:pi/2;  % x is linearly spaced values between 0 and pi/2 with increment (pi/2)/100
switch leaf
   case 'Planophile'
   y = 2 / pi * (1 + cos(2*x));
   case 'Erectophile'
   y = 2 / pi * (1 - cos(2*x));
   case 'Plagiophile'
   y = 2 / pi * (1 - cos(4*x));
   case 'Uniform'
   y = 2 / pi;
   case 'Spherical'
   y = sin(x);
end

x = x * (180/pi);           % radians -> degrees
angle = angle * (180/pi);   % radians -> degrees

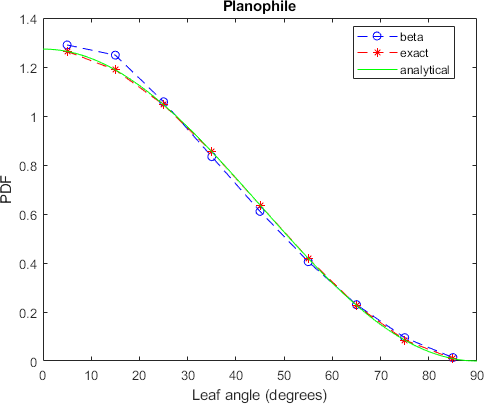
plot(angle,beta_pdf,'b--o',angle,exact_pdf,'r--*',x,y,'g')
title(leaf)
xlabel('Leaf angle (degrees)')
ylabel('PDF')
legend('beta','exact','analytical','Location','best')