Predictor–Corrector Solution for the 𝜓-Based Richards Equation

Table of contents

Code
1. Main program
2. Aux. programs
Output
1. Figures
2. Text

Code

Main program

sp_08_01.m | View on GitHub

% Supplemental program 8.1

% ---------------------------------------------------------------------
% Use the predictor-corrector method to solve the Richards equation for
% infiltration with surface soil moisture as the boundary condition.
% ---------------------------------------------------------------------

% --- Define soil layers

% Number of soil layers

soil.nsoi = 150;

% Soil layer thickness (cm)

for i = 1:soil.nsoi
   soil.dz(i) = 1.0;
end

% Soil depth (cm) at i+1/2 interface between layers i and i+1 (negative distance from surface)

soil.z_plus_onehalf(1) = -soil.dz(1);
for i = 2:soil.nsoi
   soil.z_plus_onehalf(i) = soil.z_plus_onehalf(i-1) - soil.dz(i);
end

% Soil depth (cm) at center of layer i (negative distance from surface)

soil.z(1) = 0.5 * soil.z_plus_onehalf(1);
for i = 2:soil.nsoi
   soil.z(i) = 0.5 * (soil.z_plus_onehalf(i-1) + soil.z_plus_onehalf(i));
end

% Thickness between between z(i) and z(i+1)

for i = 1:soil.nsoi-1
   soil.dz_plus_onehalf(i) = soil.z(i) - soil.z(i+1);
end
soil.dz_plus_onehalf(soil.nsoi) = 0.5 * soil.dz(soil.nsoi);

% --- Soil parameters

 soil.functions = 'van_Genuchten';  % Use van Genuchten relationships
%soil.functions = 'Campbell';       % Use Campbell relationships

switch soil.functions

   case 'Campbell'
   % example from Hornberger & Wiberg (2005, Fig. 8.3)
   ityp = 0;              % Soil texture flag
   theta_sat = 0.25;      % Volumetric water content at saturation
   psi_sat = -25.0;       % Matric potential at saturation (cm)
   bc = 0.2;              % Exponent
   Ksat = 3.4e-03;        % Hydraulic conductivity at saturation (cm/s)
   params = [theta_sat psi_sat bc Ksat ityp];

   case 'van_Genuchten'

   % Haverkamp et al. (1977): sand
   ityp = 1;              % Soil texture flag
   theta_res = 0.075;     % Residual water content
   theta_sat = 0.287;     % Volumetric water content at saturation
   vg_alpha = 0.027;      % Inverse of the air entry potential (/cm)
   vg_n = 3.96;           % Pore-size distribution index
   vg_m = 1;              % Exponent
   Ksat = 34 / 3600;      % Hydraulic conductivity at saturation (cm/s)

   % Haverkamp et al. (1977): Yolo light clay
%  ityp = 2;              % Soil texture flag
%  theta_res = 0.124;     % Residual water content
%  theta_sat = 0.495;     % Volumetric water content at saturation
%  vg_alpha = 0.026;      % Inverse of the air entry potential (/cm)
%  vg_n = 1.43;           % Pore-size distribution index
%  vg_m = 1 - 1 / vg_n;   % Exponent
%  Ksat = 0.0443 / 3600;  % Hydraulic conductivity at saturation (cm/s)

   params = [theta_res theta_sat vg_alpha vg_n vg_m Ksat ityp];
end

% --- Initial soil moisture and matric potential

for i = 1:soil.nsoi
   if (ityp == 0)
      soil.theta(i) = 0.10;
   elseif (ityp == 1)
      soil.theta(i) = 0.10;
   elseif (ityp == 2)
      soil.theta(i) = 0.24;
   end
   soil.psi(i) = matric_potential (soil.functions, params, soil.theta(i));
end

% --- Surface boundary condition: saturation (minus some small delta)

soil.theta0 = theta_sat - 1.0e-03;
if (ityp == 1)
   soil.theta0 = 0.267;
end
soil.psi0 = matric_potential (soil.functions, params, soil.theta0);

% --- Time step (seconds)

dt = 10;
if (ityp == 1)
   dt = 5;
end

% --- Length of simulation (number of time steps)

% Hornberger & Wiberg: 15, 30, or 60 minutes
if (ityp == 0)
%  ntim = 15 * 60 / dt;
%  ntim = 30 * 60 / dt;
   ntim = 60 * 60 / dt;
end

% Haverkamp et al. (1977) - sand: duration is in hours
if (ityp == 1)
%  ntim = 0.05 * 3600 / dt;
%  ntim = 0.1 * 3600 / dt;
%  ntim = 0.2 * 3600 / dt;
%  ntim = 0.3 * 3600 / dt;
%  ntim = 0.4 * 3600 / dt;
   ntim = 0.8 * 3600 / dt;
end

% Haverkamp et al. (1977) - Yolo light clay: duration is in seconds
if (ityp == 2)
%  ntim = 1.0e4 / dt;
%  ntim = 1.0e5 / dt;
%  ntim = 5.0e5 / dt;
   ntim = 1.0e6 / dt;
end

% --- Initialize accumulators for water balance check

sum_in = 0;
sum_out = 0;
sum_store = 0;

% --- Time stepping loop: NTIM iterations with a time step of DT seconds

for itim = 1:ntim

   % Hour of day

   hour = itim * (dt/86400 * 24);
   fprintf('hour = %8.3f \n',hour)

   % Calculate soil moisture

   [soil] = predictor_corrector (soil, params, dt);

   % Sum fluxes for relative mass balance error

   sum_in = sum_in + abs(soil.Q0) * dt;
   sum_out = sum_out + abs(soil.QN) * dt;
   sum_store = sum_store + soil.dtheta;

   % Save cumulative infiltration

   xout(itim) = hour;
   yout(itim) = sum_in;

end

% --- Print mass balance

fprintf('infiltration (cm) = %8.3f \n',sum_in)
fprintf('drainage (cm) = %8.3f \n',sum_out)
fprintf('storage (cm) = %8.3f \n',sum_store)
relerr = ((sum_in - sum_out) - sum_store) / (sum_in - sum_out) * 100;
fprintf('mass balance error (percent) = %8.3f \n',relerr)

% --- Graph data

plot(soil.theta,soil.z)
xlabel('Volumetric moisture content')
ylabel('Depth (cm)')

% --- Write soil moisture as output file

A = [soil.theta; soil.z];
fileID = fopen('data1.txt','w');
fprintf(fileID,'%12s %12s\n','theta','z');
fprintf(fileID,'%12.3f %12.3f\n', A);
fclose(fileID);

% --- Write cumulative infiltration as output file

B = [xout; yout];
fileID = fopen('data2.txt','w');
fprintf(fileID,'%12s %12s\n','hour','infil');
fprintf(fileID,'%12.5f %12.5f\n', B);
fclose(fileID);

Aux. programs

Campbell.m | View on GitHub

function [theta, K, cap] = Campbell (params, psi)

% -----------------------------
% Campbell (1974) relationships
% -----------------------------

% --- Soil parameters

theta_sat = params(1);    % Volumetric water content at saturation
psi_sat = params(2);      % Matric potential at saturation
b = params(3);            % Exponent
Ksat = params(4);         % Hydraulic conductivity at saturation

% --- Volumetric soil moisture (theta) for specified matric potential (psi)

if (psi <= psi_sat)
   theta = theta_sat * (psi / psi_sat)^(-1/b);
else
   theta = theta_sat;
end

% --- Hydraulic conductivity (K) for specified matric potential (psi)

if (psi <= psi_sat)
   K = Ksat * (theta / theta_sat)^(2*b+3);
else
   K = Ksat;
end

% --- Specific moisture capacity (cap) for specified matric potential (psi)

if (psi <= psi_sat)
   cap = -theta_sat / (b * psi_sat) * (psi / psi_sat)^(-1/b-1);
else
   cap = 0;
end

matric_potential.m | View on GitHub

function [psi] = matric_potential (type, params, theta)

% --- Calculate psi for a given theta

switch type
   case 'van_Genuchten'

   theta_res = params(1);    % Residual water content
   theta_sat = params(2);    % Volumetric water content at saturation
   alpha = params(3);        % Inverse of the air entry potential
   n = params(4);            % Pore-size distribution index
   m = params(5);            % Exponent

   Se = (theta - theta_res) / (theta_sat - theta_res);
   psi = -((Se^(-1/m) - 1)^(1/n)) / alpha;

   case 'Campbell'

   theta_sat = params(1);    % Volumetric water content at saturation
   psi_sat = params(2);      % Matric potential at saturation
   b = params(3);            % Exponent

   psi = psi_sat * (theta / theta_sat)^-b;

end

predictor_corrector.m | View on GitHub

function [soil] = predictor_corrector (soil, params, dt)

% -------------------------------------------------------------
% Use predictor-corrector method to solve the Richards equation
% -------------------------------------------------------------

% Input
% dt                   ! Time step (s)
% soil.nsoi            ! Number of soil layers
% soil.functions       ! van Genuchten or Campbell relationships
% soil.dz_plus_onehalf ! Thickness between between z(i) and z(i+1) (cm)
% soil.dz              ! Soil layer thickness (cm)
% soil.psi0            ! Soil surface matric potential boundary condition (cm)
%
% Input/output
% soil.theta           ! Volumetric soil moisture
% soil.psi             ! Matric potential (cm)
%
% Output
% soil.K               ! Hydraulic conductivity (cm H2O/s)
% soil.cap             ! Specific moisture capacity (/cm)
% soil.Q0              ! Infiltration flux (cm H2O/s)
% soil.QN              ! Drainage flux (cm H2O/s)
% soil.dtheta          ! Change in soil moisture (cm H2O)
% soil.err             ! Water balance error (cm H2O)

% --- Save current soil moisture and matric potential for time n

for i = 1:soil.nsoi
   theta_n(i) = soil.theta(i);
   psi_n(i) = soil.psi(i);
end

% --- Predictor step using implict solution for time n+1/2

% Hydraulic properties for current psi:
% theta - volumetric soil moisture
% K     - hydraulic conductivity
% cap   - specific moisture capacity

for i = 1:soil.nsoi
   switch soil.functions
      case 'van_Genuchten'
      [soil.theta(i), soil.K(i), soil.cap(i)] = van_Genuchten (params, soil.psi(i));
      case 'Campbell'
      [soil.theta(i), soil.K(i), soil.cap(i)] = Campbell (params, soil.psi(i));
    end
end

% Hydraulic conductivity at i+1/2 interface between layers i and i+1 is the arithmetic mean

for i = 1:soil.nsoi-1
   K_plus_onehalf(i) = 0.5 * (soil.K(i) + soil.K(i+1));
end

% Hydraulic conductivity at i=1/2 between surface (i=0) and first layer i=1

K_onehalf = soil.K(1);

% dz at i=1/2 between surface (i=0) and first layer i=1

dz_onehalf = 0.5 * soil.dz(1);

% Terms for tridiagonal matrix

i = 1;
a(i) = 0;
c(i) = -K_plus_onehalf(i) / soil.dz_plus_onehalf(i);
b(i) = soil.cap(i) * soil.dz(i) / (0.5 * dt) + K_onehalf / dz_onehalf - c(i);
d(i) = soil.cap(i) * soil.dz(i) / (0.5 * dt) * soil.psi(i) + K_onehalf / dz_onehalf * soil.psi0 + K_onehalf - K_plus_onehalf(i);

for i = 2:soil.nsoi-1
   a(i) = -K_plus_onehalf(i-1) / soil.dz_plus_onehalf(i-1);
   c(i) = -K_plus_onehalf(i) / soil.dz_plus_onehalf(i);
   b(i) = soil.cap(i) * soil.dz(i) / (0.5 * dt) - a(i) - c(i);
   d(i) = soil.cap(i) * soil.dz(i) / (0.5 * dt) * soil.psi(i) + K_plus_onehalf(i-1) - K_plus_onehalf(i);
end

i = soil.nsoi;
a(i) = -K_plus_onehalf(i-1) / soil.dz_plus_onehalf(i-1);
c(i) = 0;
b(i) = soil.cap(i) * soil.dz(i) / (0.5 * dt) - a(i) - c(i);
d(i) = soil.cap(i) * soil.dz(i) / (0.5 * dt) * soil.psi(i) + K_plus_onehalf(i-1) - soil.K(i);

% Solve for psi at n+1/2

[psi_pred] = tridiagonal_solver (a, b, c, d, soil.nsoi);

% --- Corrector step using Crank-Nicolson solution for time n+1

% Hydraulic properties for psi_pred

for i = 1:soil.nsoi
   switch soil.functions
      case 'van_Genuchten'
      [soil.theta(i), soil.K(i), soil.cap(i)] = van_Genuchten (params, psi_pred(i));
      case 'Campbell'
      [soil.theta(i), soil.K(i), soil.cap(i)] = Campbell (params, psi_pred(i));
    end
end

% Hydraulic conductivity at i+1/2 interface between layers i and i+1

for i = 1:soil.nsoi-1
   K_plus_onehalf(i) = 0.5 * (soil.K(i) + soil.K(i+1));
end

% Hydraulic conductivity at i=1/2 between surface (i=0) and first layer i=1

K_onehalf = soil.K(1);

% dz at i=1/2 between surface (i=0) and first layer i=1

dz_onehalf = 0.5 * soil.dz(1);

% Terms for tridiagonal matrix

i = 1;
a(i) = 0;
c(i) = -K_plus_onehalf(i) / (2 * soil.dz_plus_onehalf(i));
b(i) = soil.cap(i) * soil.dz(i) / dt  + K_onehalf / (2 * dz_onehalf) - c(i);
d(i) = soil.cap(i) * soil.dz(i) / dt * soil.psi(i) + K_onehalf / (2 * dz_onehalf) * soil.psi0 ...
     + K_onehalf / (2 * dz_onehalf) * (soil.psi0 - soil.psi(i)) ...
     + c(i) * (soil.psi(i) - soil.psi(i+1)) + K_onehalf - K_plus_onehalf(i);

for i = 2:soil.nsoi-1
   a(i) = -K_plus_onehalf(i-1) / (2 * soil.dz_plus_onehalf(i-1));
   c(i) = -K_plus_onehalf(i) / (2 * soil.dz_plus_onehalf(i));
   b(i) = soil.cap(i) * soil.dz(i) / dt - a(i) - c(i);
   d(i) = soil.cap(i) * soil.dz(i) / dt * soil.psi(i) - a(i) * (soil.psi(i-1) - soil.psi(i)) ...
        + c(i) * (soil.psi(i) - soil.psi(i+1)) + K_plus_onehalf(i-1) - K_plus_onehalf(i);
end

i = soil.nsoi;
a(i) = -K_plus_onehalf(i-1) / (2 * soil.dz_plus_onehalf(i-1));
c(i) = 0;
b(i) = soil.cap(i) * soil.dz(i) / dt - a(i) - c(i);
d(i) = soil.cap(i) * soil.dz(i) / dt * soil.psi(i) - a(i) * (soil.psi(i-1) - soil.psi(i)) + K_plus_onehalf(i-1) - soil.K(i);

% Solve for psi at n+1

[soil.psi] = tridiagonal_solver (a, b, c, d, soil.nsoi);

% --- Check water balance

soil.Q0 = -K_onehalf / (2 * dz_onehalf) * ((soil.psi0 - psi_n(1)) + (soil.psi0 - soil.psi(1))) - K_onehalf;
soil.QN = -soil.K(soil.nsoi);

soil.dtheta = 0;
for i = 1:soil.nsoi
   soil.dtheta = soil.dtheta + (soil.theta(i) - theta_n(i)) * soil.dz(i);
end

soil.err = soil.dtheta - (soil.QN - soil.Q0) * dt;

tridiagonal_solver.m | View on GitHub

function [u] = tridiagonal_solver (a, b, c, d, n)

% Solve for U given the set of equations R * U = D, where U is a vector
% of length N, D is a vector of length N, and R is an N x N tridiagonal
% matrix defined by the vectors A, B, C each of length N. A(1) and
% C(N) are undefined and are not referenced.
%
%     |B(1) C(1) ...  ...  ...                     |
%     |A(2) B(2) C(2) ...  ...                     |
% R = |     A(3) B(3) C(3) ...                     |
%     |                    ... A(N-1) B(N-1) C(N-1)|
%     |                    ... ...    A(N)   B(N)  |
%
% The system of equations is written as:
%
%    A_i * U_i-1 + B_i * U_i + C_i * U_i+1 = D_i
%
% for i = 1 to N. The solution is found by rewriting the
% equations so that:
%
%    U_i = F_i - E_i * U_i+1

% --- Forward sweep (1 -> N) to get E and F

e(1) = c(1) / b(1);

for i = 2: 1: n-1
   e(i) = c(i) / (b(i) - a(i) * e(i-1));
end

f(1) = d(1) / b(1);

for i = 2: 1: n
   f(i) = (d(i) - a(i) * f(i-1)) / (b(i) - a(i) * e(i-1));
end

% --- Backward substitution (N -> 1) to solve for U

u(n) = f(n);

for i = n-1: -1: 1
   u(i) = f(i) - e(i) * u(i+1);
end

van_Genuchten.m | View on GitHub

function [theta, K, cap] = van_Genuchten (params, psi)

% ----------------------------------
% van Genuchten (1980) relationships
% ----------------------------------

% --- Soil parameters

theta_res = params(1);   % Residual water content
theta_sat = params(2);   % Volumetric water content at saturation
alpha = params(3);       % Inverse of the air entry potential
n = params(4);           % Pore-size distribution index
m = params(5);           % Exponent
Ksat = params(6);        % Hydraulic conductivity at saturation
ityp = params(7);        % Soil texture flag

% --- Effective saturation (Se) for specified matric potential (psi)

if (psi <= 0)
   Se = (1 + (alpha * abs(psi))^n)^-m;
else
   Se = 1;
end

% --- Volumetric soil moisture (theta) for specified matric potential (psi)

theta = theta_res + (theta_sat - theta_res) * Se;

% --- Hydraulic conductivity (K) for specified matric potential (psi)

if (Se <= 1)
   K = Ksat * sqrt(Se) * (1 - (1 - Se^(1/m))^m)^2;

   % Special case for Haverkamp et al. (1977) sand (ityp = 1) and Yolo light clay (ityp = 2)

   if (ityp == 1)
      K = Ksat * 1.175e6 / (1.175e6 + abs(psi)^4.74);
   end
   if (ityp == 2)
      K = Ksat * 124.6/ (124.6 + abs(psi)^1.77);
   end

else

   K = Ksat;

end

% --- Specific moisture capacity (cap) for specified matric potential (psi)

if (psi <= 0)
   num = alpha * m * n * (theta_sat - theta_res) * (alpha * abs(psi))^(n-1);
   den =  (1 + (alpha * abs(psi))^n)^(m+1);
   cap = num / den;
else
   cap = 0;
end

Output

Figures

Figure 1

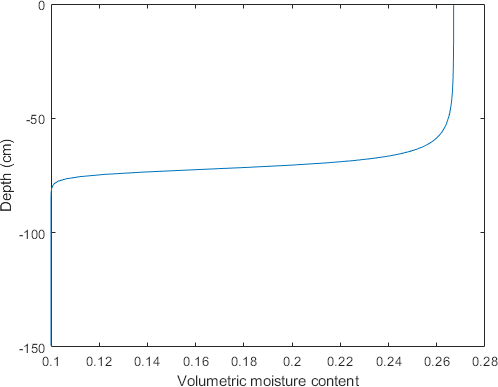
Text

data1.txt | View on GitHub | View raw

theta            z
       0.267       -0.500
       0.267       -1.500
       0.267       -2.500
       0.267       -3.500
       0.267       -4.500
       0.267       -5.500
       0.267       -6.500
       0.267       -7.500
       0.267       -8.500
       0.267       -9.500
       0.267      -10.500
       0.267      -11.500
       0.267      -12.500
       0.267      -13.500
       0.267      -14.500
       0.267      -15.500
       0.267      -16.500
       0.267      -17.500
       0.267      -18.500
       0.267      -19.500
       0.267      -20.500
       0.267      -21.500
       0.267      -22.500
       0.267      -23.500
       0.267      -24.500
       0.267      -25.500
       0.267      -26.500
       0.267      -27.500
       0.267      -28.500
       0.267      -29.500
       0.267      -30.500
       0.267      -31.500
       0.267      -32.500
       0.267      -33.500
       0.267      -34.500
       0.267      -35.500
       0.267      -36.500
       0.267      -37.500
       0.266      -38.500
       0.266      -39.500
       0.266      -40.500
       0.266      -41.500
       0.266      -42.500
       0.266      -43.500
       0.266      -44.500
       0.266      -45.500
       0.266      -46.500
       0.265      -47.500
       0.265      -48.500
       0.265      -49.500
       0.265      -50.500
       0.264      -51.500
       0.264      -52.500
       0.264      -53.500
       0.263      -54.500
       0.262      -55.500
       0.262      -56.500
       0.261      -57.500
       0.260      -58.500
       0.259      -59.500
       0.258      -60.500
       0.256      -61.500
       0.254      -62.500
       0.252      -63.500
       0.249      -64.500
       0.245      -65.500
       0.240      -66.500
       0.234      -67.500
       0.225      -68.500
       0.214      -69.500
       0.199      -70.500
       0.180      -71.500
       0.159      -72.500
       0.138      -73.500
       0.122      -74.500
       0.112      -75.500
       0.106      -76.500
       0.103      -77.500
       0.101      -78.500
       0.101      -79.500
       0.100      -80.500
       0.100      -81.500
       0.100      -82.500
       0.100      -83.500
       0.100      -84.500
       0.100      -85.500
       0.100      -86.500
       0.100      -87.500
       0.100      -88.500
       0.100      -89.500
       0.100      -90.500
       0.100      -91.500
       0.100      -92.500
       0.100      -93.500
       0.100      -94.500
       0.100      -95.500
       0.100      -96.500
       0.100      -97.500
       0.100      -98.500
       0.100      -99.500
       0.100     -100.500
       0.100     -101.500
       0.100     -102.500
       0.100     -103.500
       0.100     -104.500
       0.100     -105.500
       0.100     -106.500
       0.100     -107.500
       0.100     -108.500
       0.100     -109.500
       0.100     -110.500
       0.100     -111.500
       0.100     -112.500
       0.100     -113.500
       0.100     -114.500
       0.100     -115.500
       0.100     -116.500
       0.100     -117.500
       0.100     -118.500
       0.100     -119.500
       0.100     -120.500
       0.100     -121.500
       0.100     -122.500
       0.100     -123.500
       0.100     -124.500
       0.100     -125.500
       0.100     -126.500
       0.100     -127.500
       0.100     -128.500
       0.100     -129.500
       0.100     -130.500
       0.100     -131.500
       0.100     -132.500
       0.100     -133.500
       0.100     -134.500
       0.100     -135.500
       0.100     -136.500
       0.100     -137.500
       0.100     -138.500
       0.100     -139.500
       0.100     -140.500
       0.100     -141.500
       0.100     -142.500
       0.100     -143.500
       0.100     -144.500
       0.100     -145.500
       0.100     -146.500
       0.100     -147.500
       0.100     -148.500
       0.100     -149.500

data2.txt | View on GitHub | View raw sp_08_01_out.txt (standard output) | View on GitHub | View raw