Implicit Flux–Profile Solution
Table of contents
Code
Main program
sp_16_01.m | View on GitHub
% Supplemental program 16.1
% This code replicates the multilayer canopy model of Bonan et al. (2018)
% at US-UMB.2006 for the first time step
% --- Physical constants
physcon.vkc = 0.4; % von Karman constant
physcon.grav = 9.80665; % Gravitational acceleration (m/s2)
physcon.tfrz = 273.15; % Freezing point of water (K)
physcon.hvap = 2.501e6; % Latent heat of evaporation (J/kg)
physcon.mmh2o = 18.02 / 1000; % Molecular mass of water (kg/mol)
physcon.mmdry = 28.97 / 1000; % Molecular mass of dry air (kg/mol)
physcon.cpd = 1005; % Specific heat of dry air at constant pressure (J/kg/K)
physcon.cpw = 1846; % Specific heat of water vapor at constant pressure (J/kg/K)
physcon.rgas = 8.31446; % Universal gas constant (J/K/mol)
% --- Array indices for leaves
leafvar.nleaf = 2; % Two leaf types (sunlit and shaded)
leafvar.isun = 1; % Sunlit leaf
leafvar.isha = 2; % Shaded leaf
% --- Define canopy structure
npts = 1; % Number of grid points
for p = 1:npts
% Plant area index of canopy (m2/m2)
surfvar.pai(p) = 5.051612734794617;
% Atmospheric forcing reference height (m)
forcvar.zref(p) = 46;
% Canopy height (m)
surfvar.hc(p) = 21;
% Determine number of within-canopy layers by specifying height increment (m)
dht = 0.5;
% Define the number of within-canopy layers and adjust dht if needed
nveg = round(surfvar.hc(p) / dht);
dht = surfvar.hc(p) / nveg;
% Set array indices for within canopy layers
surfvar.nsoi(p) = 1; % First layer is soil
surfvar.nbot(p) = surfvar.nsoi(p) + 1; % Bottom leaf layer
surfvar.ntop(p) = surfvar.nbot(p) + nveg - 1; % Top leaf layer
% Calculate heights at layer interfaces (zw). These are the heights
% for the conductance between two scalar concentrations. They are
% defined for ic = nsoi (ground) to ic = ntop (top of the canopy).
ic = surfvar.ntop(p);
surfvar.zw(p,ic) = surfvar.hc(p);
for ic = surfvar.ntop(p)-1: -1: surfvar.nsoi(p)
surfvar.zw(p,ic) = surfvar.zw(p,ic+1) - dht;
end
ic = surfvar.nsoi(p);
if (surfvar.zw(p,ic) > 1e-10 || surfvar.zw(p,ic) < 0)
error('zw improperly defined at ground level')
end
% Now calculate the above-canopy layers and their heights
dz_to_zref = forcvar.zref(p) - surfvar.hc(p);
n_to_zref = round(dz_to_zref / dht);
dht = dz_to_zref / n_to_zref;
surfvar.nlev(p) = surfvar.ntop(p) + n_to_zref;
ic = surfvar.nlev(p);
surfvar.zw(p,ic) = forcvar.zref(p);
for ic = surfvar.nlev(p)-1: -1: surfvar.ntop(p)+1
surfvar.zw(p,ic) = surfvar.zw(p,ic+1) - dht;
end
% Determine heights of the scalar concentration and scalar source
% (zs). These are physically centered between the conductance points
% (i.e., in the middle of the layer).
ic = surfvar.nsoi(p);
surfvar.zs(p,ic) = 0;
for ic = surfvar.nbot(p):surfvar.nlev(p)
surfvar.zs(p,ic) = 0.5 * (surfvar.zw(p,ic) + surfvar.zw(p,ic-1));
end
% Determine plant area index increment for each layer by numerically
% integrating the plant area density (beta distribution) between
% the bottom and top heights for that layer
pbeta = 3.5; % Parameter for beta distribution
qbeta = 2.0; % Parameter for beta distribution
for ic = surfvar.nbot(p):surfvar.ntop(p)
zl = surfvar.zw(p,ic-1);
zu = surfvar.zw(p,ic);
surfvar.dpai(p,ic) = 0;
% Numerical integration between zl and zu using 100 sublayers
num_int = 100;
dz_int = (zu - zl) / num_int;
for ic_int = 1:num_int
if (ic_int == 1)
z_int = zl + 0.5 * dz_int;
else
z_int = z_int + dz_int;
end
% beta distribution probability density function
zrel = min(z_int/surfvar.hc(p), 1);
beta_pdf = (zrel^(pbeta-1) * (1 - zrel)^(qbeta-1)) / beta(pbeta,qbeta);
% Plant area density (m2/m3)
pad = (surfvar.pai(p) / surfvar.hc(p)) * beta_pdf;
% Plant area index (m2/m2)
surfvar.dpai(p,ic) = surfvar.dpai(p,ic) + pad * dz_int;
end
end
% Check to make sure sum of numerical integration matches canopy plant area index
pai_sum = 0;
for ic = surfvar.nbot(p):surfvar.ntop(p)
pai_sum = pai_sum + surfvar.dpai(p,ic);
end
if (abs(pai_sum - surfvar.pai(p)) > 1e-06)
error('plant area index error')
end
% Set layers with small plant area index to zero
pai_miss = 0;
for ic = surfvar.nbot(p):surfvar.ntop(p)
if (surfvar.dpai(p,ic) < 0.01)
pai_miss = pai_miss + surfvar.dpai(p,ic);
surfvar.dpai(p,ic) = 0;
end
end
% Distribute the missing plant area across vegetation layers
% in proportion to the plant area profile
if (pai_miss > 0)
pai_old = pai_sum;
pai_new = pai_old - pai_miss;
for ic = surfvar.nbot(p):surfvar.ntop(p)
surfvar.dpai(p,ic) = surfvar.dpai(p,ic) + pai_miss * (surfvar.dpai(p,ic) / pai_new);
end
end
% Find the lowest vegetation layer
for ic = surfvar.ntop(p): -1: surfvar.nbot(p)
if (surfvar.dpai(p,ic) > 0)
ic_bot = ic;
end
end
surfvar.nbot(p) = ic_bot;
% Zero out non-vegetation layers
ic = surfvar.nsoi(p);
surfvar.dpai(p,ic) = 0;
for ic = surfvar.ntop(p)+1:surfvar.nlev(p)
surfvar.dpai(p,ic) = 0;
end
end
% --- Canopy layer variables
for p = 1:npts
% Wet and dry fraction of each layer
for ic = surfvar.nbot(p):surfvar.ntop(p)
surfvar.fwet(p,ic) = 0;
surfvar.fdry(p,ic) = 0.8218390792391702;
end
% Sunlit and shaded fraction of each layer
Kb = 1.762817445019839;
for ic = surfvar.ntop(p): -1: surfvar.nbot(p)
if (ic == surfvar.ntop(p))
sumpai = 0.5 * surfvar.dpai(p,ic);
else
sumpai = sumpai + 0.5 * (surfvar.dpai(p,ic+1) + surfvar.dpai(p,ic));
end
surfvar.fracsun(p,ic) = exp(-Kb * sumpai);
surfvar.fracsha(p,ic) = 1 - surfvar.fracsun(p,ic);
end
% Leaf conductances of each layer - specify boundary layer and stomatal conductances rather than calculate
for ic = surfvar.nbot(p):surfvar.ntop(p)
leafvar.gbh(p,ic,leafvar.isun) = 2.268731551029694;
leafvar.gbh(p,ic,leafvar.isha) = 2.268731551029694;
leafvar.gbv(p,ic,leafvar.isun) = 2.496430918408511;
leafvar.gbv(p,ic,leafvar.isha) = 2.496430918408511;
end
ic = 7; leafvar.gs(p,ic,leafvar.isun) = 0.1056193510550169; leafvar.gs(p,ic,leafvar.isha) = 2.0000000000000000E-003;
ic = 8; leafvar.gs(p,ic,leafvar.isun) = 0.1058669704208841; leafvar.gs(p,ic,leafvar.isha) = 2.0000000000000000E-003;
ic = 9; leafvar.gs(p,ic,leafvar.isun) = 0.1062166035088956; leafvar.gs(p,ic,leafvar.isha) = 2.0000000000000000E-003;
ic = 10; leafvar.gs(p,ic,leafvar.isun) = 0.1066846074875817; leafvar.gs(p,ic,leafvar.isha) = 2.0000000000000000E-003;
ic = 11; leafvar.gs(p,ic,leafvar.isun) = 0.1072854387286280; leafvar.gs(p,ic,leafvar.isha) = 2.0000000000000000E-003;
ic = 12; leafvar.gs(p,ic,leafvar.isun) = 0.1080315168674592; leafvar.gs(p,ic,leafvar.isha) = 2.0000000000000000E-003;
ic = 13; leafvar.gs(p,ic,leafvar.isun) = 0.1089335362366439; leafvar.gs(p,ic,leafvar.isha) = 2.0000000000000000E-003;
ic = 14; leafvar.gs(p,ic,leafvar.isun) = 0.1100012607812562; leafvar.gs(p,ic,leafvar.isha) = 2.0000000000000000E-003;
ic = 15; leafvar.gs(p,ic,leafvar.isun) = 0.1112447128077408; leafvar.gs(p,ic,leafvar.isha) = 2.0000000000000000E-003;
ic = 16; leafvar.gs(p,ic,leafvar.isun) = 0.1126755044648808; leafvar.gs(p,ic,leafvar.isha) = 2.0000000000000000E-003;
ic = 17; leafvar.gs(p,ic,leafvar.isun) = 0.1138467165585616; leafvar.gs(p,ic,leafvar.isha) = 2.0000000000000000E-003;
ic = 18; leafvar.gs(p,ic,leafvar.isun) = 0.1170524695200598; leafvar.gs(p,ic,leafvar.isha) = 2.0000000000000000E-003;
ic = 19; leafvar.gs(p,ic,leafvar.isun) = 0.1186451281076514; leafvar.gs(p,ic,leafvar.isha) = 2.0000000000000000E-003;
ic = 20; leafvar.gs(p,ic,leafvar.isun) = 0.1206859738130298; leafvar.gs(p,ic,leafvar.isha) = 2.0000000000000000E-003;
ic = 21; leafvar.gs(p,ic,leafvar.isun) = 0.1228219389652392; leafvar.gs(p,ic,leafvar.isha) = 2.0000000000000000E-003;
ic = 22; leafvar.gs(p,ic,leafvar.isun) = 0.1263235652964973; leafvar.gs(p,ic,leafvar.isha) = 2.0000000000000000E-003;
ic = 23; leafvar.gs(p,ic,leafvar.isun) = 0.1300019677357508; leafvar.gs(p,ic,leafvar.isha) = 2.0000000000000000E-003;
ic = 24; leafvar.gs(p,ic,leafvar.isun) = 0.1322680545506565; leafvar.gs(p,ic,leafvar.isha) = 5.2146013029975334E-003;
ic = 25; leafvar.gs(p,ic,leafvar.isun) = 0.1367071935229807; leafvar.gs(p,ic,leafvar.isha) = 5.5227688387169205E-003;
ic = 26; leafvar.gs(p,ic,leafvar.isun) = 0.1408216759258680; leafvar.gs(p,ic,leafvar.isha) = 9.2945439124555301E-003;
ic = 27; leafvar.gs(p,ic,leafvar.isun) = 0.1452273039039047; leafvar.gs(p,ic,leafvar.isha) = 9.4101275089266447E-003;
ic = 28; leafvar.gs(p,ic,leafvar.isun) = 0.1499262843535941; leafvar.gs(p,ic,leafvar.isha) = 1.2582674218550544E-002;
ic = 29; leafvar.gs(p,ic,leafvar.isun) = 0.1549264640058029; leafvar.gs(p,ic,leafvar.isha) = 1.6999874421743270E-002;
ic = 30; leafvar.gs(p,ic,leafvar.isun) = 0.1611234013632947; leafvar.gs(p,ic,leafvar.isha) = 2.3036435105984941E-002;
ic = 31; leafvar.gs(p,ic,leafvar.isun) = 0.1668845999057947; leafvar.gs(p,ic,leafvar.isha) = 2.7903866816023401E-002;
ic = 32; leafvar.gs(p,ic,leafvar.isun) = 0.1727971327085968; leafvar.gs(p,ic,leafvar.isha) = 3.7385308959493969E-002;
ic = 33; leafvar.gs(p,ic,leafvar.isun) = 0.1788628079180081; leafvar.gs(p,ic,leafvar.isha) = 4.6808450662473224E-002;
ic = 34; leafvar.gs(p,ic,leafvar.isun) = 0.1850771375553107; leafvar.gs(p,ic,leafvar.isha) = 5.9036977283335762E-002;
ic = 35; leafvar.gs(p,ic,leafvar.isun) = 0.1934140277837149; leafvar.gs(p,ic,leafvar.isha) = 7.1890808689035093E-002;
ic = 36; leafvar.gs(p,ic,leafvar.isun) = 0.1998116684650200; leafvar.gs(p,ic,leafvar.isha) = 8.7547774703355410E-002;
ic = 37; leafvar.gs(p,ic,leafvar.isun) = 0.2061626747018590; leafvar.gs(p,ic,leafvar.isha) = 0.1059444058487105;
ic = 38; leafvar.gs(p,ic,leafvar.isun) = 0.2124795008223110; leafvar.gs(p,ic,leafvar.isha) = 0.1228398700721039;
ic = 39; leafvar.gs(p,ic,leafvar.isun) = 0.2173241738995193; leafvar.gs(p,ic,leafvar.isha) = 0.1416660859387607;
ic = 40; leafvar.gs(p,ic,leafvar.isun) = 0.2228796106202699; leafvar.gs(p,ic,leafvar.isha) = 0.1584170776550386;
ic = 41; leafvar.gs(p,ic,leafvar.isun) = 0.2272584280787935; leafvar.gs(p,ic,leafvar.isha) = 0.1712280540285039;
ic = 42; leafvar.gs(p,ic,leafvar.isun) = 0.2303662043528620; leafvar.gs(p,ic,leafvar.isha) = 0.1801048624092090;
ic = 43; leafvar.gs(p,ic,leafvar.isun) = 0.2315636153119537; leafvar.gs(p,ic,leafvar.isha) = 0.1844507421254655;
% Net radiation of each leaf - specify Rn rather than calculate
% for ic = surfvar.nbot(p):surfvar.ntop(p)
% leafvar.rnleaf(p,ic,leafvar.isun) = ...;
% leafvar.rnleaf(p,ic,leafvar.isha) = ...;
% end
ic = 7; leafvar.rnleaf(p,ic,leafvar.isun) = 139.9869857739781; leafvar.rnleaf(p,ic,leafvar.isha) = 1.411488333307743;
ic = 8; leafvar.rnleaf(p,ic,leafvar.isun) = 139.8100113537029; leafvar.rnleaf(p,ic,leafvar.isha) = 1.234513913032590;
ic = 9; leafvar.rnleaf(p,ic,leafvar.isun) = 139.7147998761629; leafvar.rnleaf(p,ic,leafvar.isha) = 1.139302435492522;
ic = 10; leafvar.rnleaf(p,ic,leafvar.isun) = 139.6645467566822; leafvar.rnleaf(p,ic,leafvar.isha) = 1.089049316011852;
ic = 11; leafvar.rnleaf(p,ic,leafvar.isun) = 139.6422035725484; leafvar.rnleaf(p,ic,leafvar.isha) = 1.066706131878055;
ic = 12; leafvar.rnleaf(p,ic,leafvar.isun) = 139.6392966303582; leafvar.rnleaf(p,ic,leafvar.isha) = 1.063799189687813;
ic = 13; leafvar.rnleaf(p,ic,leafvar.isun) = 139.6514847604817; leafvar.rnleaf(p,ic,leafvar.isha) = 1.075987319811279;
ic = 14; leafvar.rnleaf(p,ic,leafvar.isun) = 139.6766021357984; leafvar.rnleaf(p,ic,leafvar.isha) = 1.101104695127997;
ic = 15; leafvar.rnleaf(p,ic,leafvar.isun) = 139.7137254254163; leafvar.rnleaf(p,ic,leafvar.isha) = 1.138227984745972;
ic = 16; leafvar.rnleaf(p,ic,leafvar.isun) = 139.7627019640728; leafvar.rnleaf(p,ic,leafvar.isha) = 1.187204523402388;
ic = 17; leafvar.rnleaf(p,ic,leafvar.isun) = 139.8238999626867; leafvar.rnleaf(p,ic,leafvar.isha) = 1.248402522016342;
ic = 18; leafvar.rnleaf(p,ic,leafvar.isun) = 139.8980702313243; leafvar.rnleaf(p,ic,leafvar.isha) = 1.322572790653995;
ic = 19; leafvar.rnleaf(p,ic,leafvar.isun) = 139.9862631887909; leafvar.rnleaf(p,ic,leafvar.isha) = 1.410765748120540;
ic = 20; leafvar.rnleaf(p,ic,leafvar.isun) = 140.0897684653183; leafvar.rnleaf(p,ic,leafvar.isha) = 1.514271024647946;
ic = 21; leafvar.rnleaf(p,ic,leafvar.isun) = 140.2100538053315; leafvar.rnleaf(p,ic,leafvar.isha) = 1.634556364661143;
ic = 22; leafvar.rnleaf(p,ic,leafvar.isun) = 140.3486818847138; leafvar.rnleaf(p,ic,leafvar.isha) = 1.773184444043382;
ic = 23; leafvar.rnleaf(p,ic,leafvar.isun) = 140.5071806149416; leafvar.rnleaf(p,ic,leafvar.isha) = 1.931683174271291;
ic = 24; leafvar.rnleaf(p,ic,leafvar.isun) = 140.6868352048059; leafvar.rnleaf(p,ic,leafvar.isha) = 2.111337764135555;
ic = 25; leafvar.rnleaf(p,ic,leafvar.isun) = 140.8883584829672; leafvar.rnleaf(p,ic,leafvar.isha) = 2.312861042296822;
ic = 26; leafvar.rnleaf(p,ic,leafvar.isun) = 141.1113792315132; leafvar.rnleaf(p,ic,leafvar.isha) = 2.535881790842842;
ic = 27; leafvar.rnleaf(p,ic,leafvar.isun) = 141.3536664423189; leafvar.rnleaf(p,ic,leafvar.isha) = 2.778169001648555;
ic = 28; leafvar.rnleaf(p,ic,leafvar.isun) = 141.6099822011559; leafvar.rnleaf(p,ic,leafvar.isha) = 3.034484760485563;
ic = 29; leafvar.rnleaf(p,ic,leafvar.isun) = 141.8704336551236; leafvar.rnleaf(p,ic,leafvar.isha) = 3.294936214453243;
ic = 30; leafvar.rnleaf(p,ic,leafvar.isun) = 142.1181913093900; leafvar.rnleaf(p,ic,leafvar.isha) = 3.542693868719610;
ic = 31; leafvar.rnleaf(p,ic,leafvar.isun) = 142.3264909566734; leafvar.rnleaf(p,ic,leafvar.isha) = 3.750993516003037;
ic = 32; leafvar.rnleaf(p,ic,leafvar.isun) = 142.4550034158019; leafvar.rnleaf(p,ic,leafvar.isha) = 3.879505975131512;
ic = 33; leafvar.rnleaf(p,ic,leafvar.isun) = 142.4460421185886; leafvar.rnleaf(p,ic,leafvar.isha) = 3.870544677918208;
ic = 34; leafvar.rnleaf(p,ic,leafvar.isun) = 142.2218178601452; leafvar.rnleaf(p,ic,leafvar.isha) = 3.646320419474797;
ic = 35; leafvar.rnleaf(p,ic,leafvar.isun) = 141.6851596824207; leafvar.rnleaf(p,ic,leafvar.isha) = 3.109662241750371;
ic = 36; leafvar.rnleaf(p,ic,leafvar.isun) = 140.7277716843982; leafvar.rnleaf(p,ic,leafvar.isha) = 2.152274243727867;
ic = 37; leafvar.rnleaf(p,ic,leafvar.isun) = 139.2518034108234; leafvar.rnleaf(p,ic,leafvar.isha) = 0.676305970153017;
ic = 38; leafvar.rnleaf(p,ic,leafvar.isun) = 137.2114197261891; leafvar.rnleaf(p,ic,leafvar.isha) = -1.364077714481233;
ic = 39; leafvar.rnleaf(p,ic,leafvar.isun) = 134.6805463548995; leafvar.rnleaf(p,ic,leafvar.isha) = -3.894951085770870;
ic = 40; leafvar.rnleaf(p,ic,leafvar.isun) = 131.9550915266485; leafvar.rnleaf(p,ic,leafvar.isha) = -6.620405914021802;
ic = 41; leafvar.rnleaf(p,ic,leafvar.isun) = 129.7361873094630; leafvar.rnleaf(p,ic,leafvar.isha) = -8.839310131207370;
ic = 42; leafvar.rnleaf(p,ic,leafvar.isun) = 129.7993862020948; leafvar.rnleaf(p,ic,leafvar.isha) = -8.776111238575538;
ic = 43; leafvar.rnleaf(p,ic,leafvar.isun) = 143.7045065806239; leafvar.rnleaf(p,ic,leafvar.isha) = 5.129009139953610;
% Leaf heat capacity
for ic = surfvar.nbot(p):surfvar.ntop(p)
leafvar.cpleaf(p,ic) = 744.5333333333334;
end
end
% --- Soil variables
for p = 1:npts
soilvar.tk(p) = 1.261326601469150; % Soil thermal conductivity (W/m/K)
soilvar.dz(p) = 7.1006354171935350E-003; % Soil layer depth (m)
soilvar.tsoi(p) = 294.8492736816406; % Soil temperature (K)
soilvar.resis(p) = 3361.509423807650; % Soil evaporative resistance (s/m)
soilvar.rhg(p) = 0.9984057411945876; % Relative humidity of airspace at soil surface (fraction)
fluxvar.rnsoi(p) = 1.896127799819662; % Net radiation at ground (W/m2)
end
% --- Atmospheric forcing at a reference height
for p = 1:npts
forcvar.pref(p) = 98620; % Atmospheric pressure (Pa)
forcvar.uref(p) = 5.169; % Wind speed at reference height (m/s)
forcvar.tref(p) = 295.9349938964844; % Air temperature at reference height (K)
% Water vapor (mol/mol) using constant relative humidity
relhum = 53.871;
[esat, desat] = satvap (forcvar.tref(p)-physcon.tfrz);
eref = (relhum / 100) * esat;
forcvar.qref(p) = eref / forcvar.pref(p);
% Specific humidity (kg/kg)
qref_kg_kg = physcon.mmh2o / physcon.mmdry * eref / (forcvar.pref(p) - (1 - physcon.mmh2o/physcon.mmdry) * eref);
% Potential temperature and virtual potential temperature (K)
forcvar.thref(p) = forcvar.tref(p) + 0.0098 * forcvar.zref(p);
forcvar.thvref(p) = forcvar.thref(p) * (1 + 0.61 * qref_kg_kg);
% Molar density (mol/m3)
forcvar.rhomol(p) = forcvar.pref(p) / (physcon.rgas * forcvar.tref(p));
% Air density (kg/m3)
rhoair = forcvar.rhomol(p) * physcon.mmdry * (1 - (1 - physcon.mmh2o/physcon.mmdry) * eref / forcvar.pref(p));
% Molecular mass of air (kg/mol)
forcvar.mmair(p) = rhoair / forcvar.rhomol(p);
% Specific heat of air at constant pressure (J/mol/K)
forcvar.cpair(p) = physcon.cpd * (1 + (physcon.cpw/physcon.cpd - 1) * qref_kg_kg) * forcvar.mmair(p);
end
% --- Time step (s)
dt = 5 * 60;
% --- Initialize profiles
for p = 1:npts
for ic = surfvar.nsoi(p):surfvar.nlev(p)
fluxvar.tair_old(p,ic) = forcvar.tref(p);
fluxvar.qair_old(p,ic) = forcvar.qref(p);
fluxvar.tveg_old(p,ic,leafvar.isun) = forcvar.tref(p);
fluxvar.tveg_old(p,ic,leafvar.isha) = forcvar.tref(p);
end
fluxvar.taf(p) = fluxvar.tair_old(p,surfvar.ntop(p));
fluxvar.qaf(p) = fluxvar.qair_old(p,surfvar.ntop(p));
end
% Initialize profile output variables
for p = 1:npts
for ic = surfvar.nsoi(p):surfvar.nlev(p)
fluxvar.wind(p,ic) = 0;
fluxvar.tair(p,ic) = 0;
fluxvar.qair(p,ic) = 0;
fluxvar.tveg(p,ic,leafvar.isun) = 0;
fluxvar.tveg(p,ic,leafvar.isha) = 0;
fluxvar.ga_prof(p,ic) = 0;
end
for ic = surfvar.nbot(p):surfvar.ntop(p)
fluxvar.shveg(p,ic) = 0;
fluxvar.etveg(p,ic) = 0;
fluxvar.stveg(p,ic) = 0;
end
for ic = surfvar.nbot(p):surfvar.nlev(p)
fluxvar.shair(p,ic) = 0;
fluxvar.etair(p,ic) = 0;
fluxvar.stair(p,ic) = 0;
end
end
% --- Calculate fluxes and scalar profiles
for p = 1:npts
surfvar.p = p;
[fluxvar] = canopy_turbulence (dt, physcon, forcvar, surfvar, leafvar, soilvar, fluxvar);
end
% --- Write profile output data
p = 1;
for ic = surfvar.nsoi(p):surfvar.nlev(p)
fprintf('%6.0f %10.3f %10.3f %10.3f %10.3f %10.3f %10.3f %10.3f\n',ic-1,surfvar.zs(p,ic),surfvar.dpai(p,ic), ...
fluxvar.wind(p,ic),fluxvar.tair(p,ic),fluxvar.qair(p,ic)*forcvar.pref(p), ...
fluxvar.tveg(p,ic,leafvar.isun),fluxvar.tveg(p,ic,leafvar.isha))
end
% --- Make graph profile output data
p = 1;
z = surfvar.zs(p,:) / surfvar.hc(p);
x = fluxvar.tair(p,:) - 273.15;
plot(x,z)
title('Profiles')
xlabel('Air temperature (^oC)')
ylabel('Relative height')
Aux. programs
brent_root.m | View on GitHub
function [fluxvar, root] = brent_root (func, physcon, forcvar, surfvar, fluxvar, xa, xb, tol)
% Use Brent's method to find the root of a function, which is known to exist between
% xa and xb. The root is updated until its accuracy is tol. func is the name of the
% function to solve. The variable root is returned as the root of the function. The
% function being evaluated has the definition statement:
%
% function [fluxvar, fx] = func (physcon, forcvar, surfvar, fluxvar, x)
%
% The function func is exaluated at x and the returned value is fx. It uses variables
% in the physcon, forcvar, surfvar, and fluxvar structures. These are passed in as
% input arguments. It also calculates values for variables in the fluxvar structure
% so this must be returned in the function call as an output argument. The matlab
% function feval evaluates func.
% --- Evaluate func at xa and xb and make sure the root is bracketed
a = xa;
b = xb;
[fluxvar, fa] = feval(func, physcon, forcvar, surfvar, fluxvar, a);
[fluxvar, fb] = feval(func, physcon, forcvar, surfvar, fluxvar, b);
if ((fa > 0 & fb > 0) | (fa < 0 & fb < 0))
error('brent_root error: root must be bracketed')
end
% --- Initialize iteration
itmax = 50; % Maximum number of iterations
eps1 = 1e-08; % Relative error tolerance
c = b;
fc = fb;
% --- Iterative root calculation
for iter = 1:itmax
if ((fb > 0 & fc > 0) | (fb < 0 & fc < 0))
c = a;
fc = fa;
d = b - a;
e = d;
end
if (abs(fc) < abs(fb))
a = b;
b = c;
c = a;
fa = fb;
fb = fc;
fc = fa;
end
tol1 = 2 * eps1 * abs(b) + 0.5 * tol;
xm = 0.5 * (c - b);
% Check to end iteration
if (abs(xm) <= tol1 | fb == 0)
break
end
if (abs(e) >= tol1 & abs(fa) > abs(fb))
s = fb / fa;
if (a == c)
p = 2 * xm * s;
q = 1 - s;
else
q = fa / fc;
r = fb / fc;
p = s * (2 * xm * q * (q - r) - (b - a) * (r - 1));
q = (q - 1) * (r - 1) * (s - 1);
end
if (p > 0)
q = -q;
end
p = abs(p);
if (2*p < min(3*xm*q-abs(tol1*q), abs(e*q)))
e = d;
d = p / q;
else
d = xm;
e = d;
end
else
d = xm;
e = d;
end
a = b;
fa = fb;
if (abs(d) > tol1)
b = b + d;
else
if (xm >= 0)
b = b + abs(tol1);
else
b = b - abs(tol1);
end
end
[fluxvar, fb] = feval(func, physcon, forcvar, surfvar, fluxvar, b);
% Check to end iteration
if (fb == 0)
break
end
% Check to see if failed to converge
if (iter == itmax)
error('brent_root error: Maximum number of interations exceeded')
end
end
root = b;
canopy_turbulence.m | View on GitHub
function [fluxvar] = canopy_turbulence (dt, physcon, forcvar, surfvar, leafvar, soilvar, fluxvar)
% Canopy turbulence, aeorodynamic conductances, and wind/temperature/water vapor
% profiles using above- and within-canopy coupling with a roughness sublayer
% (RSL) parameterization
% ------------------------------------------------------------------------------------
% Input
% dt ! Model time step (s)
% physcon.vkc ! von Karman constant
% physcon.grav ! Gravitational acceleration (m/s2)
% physcon.mmh2o ! Molecular mass of water (kg/mol)
% physcon.tfrz ! Freezing point of water (K)
% physcon.hvap ! Latent heat of evaporation (J/kg)
%
% forcvar.zref ! Reference height (m)
% forcvar.uref ! Wind speed at reference height (m/s)
% forcvar.thref ! Potential temperature at reference height (K)
% forcvar.thvref ! Virtual potential temperature at reference height (K)
% forcvar.qref ! Water vapor at reference height (mol/mol)
% forcvar.pref ! Atmospheric pressure (Pa)
% forcvar.mmair ! Molecular mass of air at reference height (kg/mol)
% forcvar.cpair ! Specific heat of air at constant pressure (J/mol/K)
% forcvar.rhomol ! Molar density (mol/m3)
%
% surfvar.p ! Index for grid point to process
% surfvar.hc ! Canopy height (m)
% surfvar.pai ! Canopy plant area index (m2/m2)
% surfvar.nlev ! Index for top level
% surfvar.ntop ! Index for top leaf layer
% surfvar.nsoi ! First canopy layer is soil
% surfvar.zs ! Canopy height for scalar concentration and source (m)
% surfvar.zw ! Canopy height at layer interfaces (m)
% surfvar.dpai ! Layer plant area index (m2/m2)
% surfvar.fwet ! Fraction of plant area index that is wet
% surfvar.fdry ! Fraction of plant area index that is green and dry
% surfvar.fracsun ! Sunlit fraction of canopy layer
% surfvar.fracsha ! Shaded fraction of canopy layer
%
% leafvar.nleaf ! Number of leaf types (sunlit and shaded)
% leafvar.isun ! Sunlit leaf index
% leafvar.isha ! Shaded leaf index
% leafvar.gbh ! Leaf boundary layer conductance, heat (mol/m2 leaf/s)
% leafvar.gbv ! Leaf boundary layer conductance, H2O (mol H2O/m2 leaf/s)
% leafvar.gs ! Leaf stomatal conductance (mol H2O/m2 leaf/s)
% leafvar.cpleaf ! Leaf heat capacity (J/m2 leaf/K)
% leafvar.rnleaf ! Leaf net radiation (W/m2 leaf)
%
% soilvar.tk ! Soil thermal conductivity (W/m/K)
% soilvar.dz ! Soil layer depth (m)
% soilvar.tsoi ! Soil temperature (K)
% soilvar.resis ! Soil evaporative resistance (s/m)
% soilvar.rhg ! Relative humidity of airspace at soil surface (fraction)
%
% fluxvar.rnsoi ! Net radiation at ground (W/m2)
% fluxvar.tair_old ! Air temperature profile for previous timestep (K)
% fluxvar.qair_old ! Water vapor profile for previous timestep (mol/mol)
% fluxvar.tveg_old ! Vegetation temperature profile for previous timestep (K)
%
% Input/output
% fluxvar.taf ! Air temperature at canopy top (K)
% fluxvar.qaf ! Water vapor at canopy top (mol/mol)
%
% Output (specific to canopy_turbulence)
% fluxvar.Lc ! Canopy density length scale (m)
% fluxvar.wind ! Wind speed profile (m/s)
% fluxvar.uaf ! Wind speed at canopy top (m/s)
% fluxvar.ga_prof ! Canopy layer aerodynamic conductance for scalars (mol/m2/s)
%
% Output (from obukhov_function)
% fluxvar.c1m ! Roughness sublayer c1 parameter for momentum (dimensionless)
% fluxvar.c1c ! Roughness sublayer c1 parameter for scalars (dimensionless)
% fluxvar.c2 ! Roughness sublayer depth scale multiplier (dimensionless)
% fluxvar.disp ! Displacement height (m)
% fluxvar.beta ! u* / u(hc)
% fluxvar.PrSc ! Prandtl (Schmidt) number at canopy top
% fluxvar.ustar ! Friction velocity (m/s)
% fluxvar.tstar ! Temperature scale (K)
% fluxvar.qstar ! Water vapor scale (mol/mol)
% fluxvar.gac ! Aerodynamic conductance for a scalar above canopy (mol/m2/s)
% fluxvar.obu_ustar ! Obukhov length used for u* (m)
% fluxvar.obu ! Value for Obukhov length (m)
%
% Output (from scalar_profile)
% fluxvar.tair ! Air temperature profile (K)
% fluxvar.qair ! Water vapor profile (mol/mol)
% fluxvar.tveg ! Vegetation temperature profile (K)
% fluxvar.shsoi ! Ground sensible heat flux, ground (W/m2)
% fluxvar.etsoi ! Ground evaporation flux (mol H2O/m2/s)
% fluxvar.gsoi ! Soil heat flux (W/m2)
% fluxvar.tg ! Soil surface temperature (K)
% fluxvar.shveg ! Leaf sensible heat flux (W/m2 leaf)
% fluxvar.etveg ! Leaf evapotranspiration flux (mol H2O/m2 leaf/s)
% fluxvar.stveg ! Leaf storage heat flux (W/m2 leaf)
% fluxvar.shair ! Canopy air sensible heat flux (W/m2)
% fluxvar.etair ! Canopy air water vapor flux (mol H2O/m2/s)
% fluxvar.stair ! Canopy air storage heat flux (W/m2)
% ------------------------------------------------------------------------------------
% --- Index for grid point to process
p = surfvar.p;
% --- Leaf drag coefficient (dimensionless)
cd = 0.25;
% --- Canopy density length scale (m)
fluxvar.Lc(p) = surfvar.hc(p) / (cd * surfvar.pai(p));
% --- Calculate the Obukhov length
% Calculate the Obukhov length (obu) for the current surface temperature
% and surface vapor pressure using Harman & Finnigan (2007, 2008) roughness
% sublayer (RSL) theory. Use the function "obukhov_function" to iterate obu
% until the change in obu is less than tol.
obu0 = 100; % Initial estimate for Obukhov length (m)
obu1 = -100; % Initial estimate for Obukhov length (m)
tol = 0.01; % Accuracy tolerance for Obukhov length (m)
func_name = 'obukhov_function'; % The function is the file obukhov_function.m
% Solve for the Obukhov length. Do not use final returned value for obu.
% Instead, use the value used to calculate u*
[fluxvar, oburoot] = hybrid_root (func_name, physcon, forcvar, surfvar, fluxvar, obu0, obu1, tol);
fluxvar.obu(p) = fluxvar.obu_ustar(p);
% --- Wind profile (m/s)
% Above-canopy wind speed: defined at zs
h_minus_d = surfvar.hc(p) - fluxvar.disp(p);
[psi_m_hc] = psi_m_monin_obukhov (h_minus_d / fluxvar.obu(p));
[psi_m_rsl_hc] = psi_m_rsl (h_minus_d, h_minus_d, fluxvar.obu(p), fluxvar.c1m(p), fluxvar.c2);
for ic = surfvar.ntop(p)+1:surfvar.nlev(p)
z_minus_d = surfvar.zs(p,ic) - fluxvar.disp(p);
[psi_m_zs] = psi_m_monin_obukhov (z_minus_d / fluxvar.obu(p));
[psi_m_rsl_zs] = psi_m_rsl (z_minus_d, h_minus_d, fluxvar.obu(p), fluxvar.c1m(p), fluxvar.c2);
psim = -psi_m_zs + psi_m_hc + psi_m_rsl_zs - psi_m_rsl_hc + physcon.vkc / fluxvar.beta(p);
fluxvar.wind(p,ic) = fluxvar.ustar(p) / physcon.vkc * (log(z_minus_d/h_minus_d) + psim);
end
% Wind speed at top of canopy
fluxvar.uaf(p) = fluxvar.ustar(p) / fluxvar.beta(p);
% Within-canopy wind speed: defined at zs. Limit to > 0.1 m/s
lm = 2 * fluxvar.beta(p)^3 * fluxvar.Lc(p);
lm_over_beta = lm / fluxvar.beta(p);
for ic = surfvar.nsoi(p)+1:surfvar.ntop(p)
fluxvar.wind(p,ic) = fluxvar.uaf(p) * exp((surfvar.zs(p,ic) - surfvar.hc(p)) / lm_over_beta);
fluxvar.wind(p,ic) = max(fluxvar.wind(p,ic), 0.1);
end
% Wind speed at ground
fluxvar.wind(p,surfvar.nsoi(p)) = 0;
% --- Aerodynamic conductances (mol/m2/s) between zs(i) and zs(i+1)
% Above-canopy conductances
h_minus_d = surfvar.hc(p) - fluxvar.disp(p);
[psi_c_hc] = psi_c_monin_obukhov (h_minus_d / fluxvar.obu(p));
[psi_c_rsl_hc] = psi_c_rsl (h_minus_d, h_minus_d, fluxvar.obu(p), fluxvar.c1c(p), fluxvar.c2);
for ic = surfvar.ntop(p)+1:surfvar.nlev(p)-1
% Lower height zs(i)
z_minus_d = surfvar.zs(p,ic) - fluxvar.disp(p);
[psi_c_zs] = psi_c_monin_obukhov (z_minus_d / fluxvar.obu(p));
[psi_c_rsl_zs] = psi_c_rsl (z_minus_d, h_minus_d, fluxvar.obu(p), fluxvar.c1c(p), fluxvar.c2);
psic1 = -psi_c_zs + psi_c_hc + psi_c_rsl_zs - psi_c_rsl_hc;
% Upper height zs(i+1)
z_minus_d = surfvar.zs(p,ic+1) - fluxvar.disp(p);
[psi_c_zs] = psi_c_monin_obukhov (z_minus_d / fluxvar.obu(p));
[psi_c_rsl_zs] = psi_c_rsl (z_minus_d, h_minus_d, fluxvar.obu(p), fluxvar.c1c(p), fluxvar.c2);
psic2 = -psi_c_zs + psi_c_hc + psi_c_rsl_zs - psi_c_rsl_hc;
% Conductance. Note that psic = psic2 - psic1 is equivalent to:
% -psi_c_z2 + psi_c_z1 + psi_c_rsl_z2 - psi_c_rsl_z1
psic = psic2 - psic1;
zlog = log((surfvar.zs(p,ic+1)-fluxvar.disp(p)) / (surfvar.zs(p,ic)-fluxvar.disp(p)));
fluxvar.ga_prof(p,ic) = forcvar.rhomol(p) * physcon.vkc * fluxvar.ustar(p) / (zlog + psic);
end
% Special case for the top layer to the reference height
ic = surfvar.nlev(p);
z_minus_d = surfvar.zs(p,ic) - fluxvar.disp(p);
[psi_c_zs] = psi_c_monin_obukhov (z_minus_d / fluxvar.obu(p));
[psi_c_rsl_zs] = psi_c_rsl (z_minus_d, h_minus_d, fluxvar.obu(p), fluxvar.c1c(p), fluxvar.c2);
psic1 = -psi_c_zs + psi_c_hc + psi_c_rsl_zs - psi_c_rsl_hc;
z_minus_d = forcvar.zref(p) - fluxvar.disp(p);
[psi_c_zs] = psi_c_monin_obukhov (z_minus_d / fluxvar.obu(p));
[psi_c_rsl_zs] = psi_c_rsl (z_minus_d, h_minus_d, fluxvar.obu(p), fluxvar.c1c(p), fluxvar.c2);
psic2 = -psi_c_zs + psi_c_hc + psi_c_rsl_zs - psi_c_rsl_hc;
psic = psic2 - psic1;
zlog = log((forcvar.zref(p)-fluxvar.disp(p)) / (surfvar.zs(p,ic)-fluxvar.disp(p)));
fluxvar.ga_prof(p,ic) = forcvar.rhomol(p) * physcon.vkc * fluxvar.ustar(p) / (zlog + psic);
% Within-canopy aerodynamic conductances
for ic = surfvar.nsoi(p)+1:surfvar.ntop(p)-1
zl = surfvar.zs(p,ic) - surfvar.hc(p);
zu = surfvar.zs(p,ic+1) - surfvar.hc(p);
res = fluxvar.PrSc(p) / (fluxvar.beta(p) * fluxvar.ustar(p)) * (exp(-zl/lm_over_beta) - exp(-zu/lm_over_beta));
fluxvar.ga_prof(p,ic) = forcvar.rhomol(p) / res;
end
% Special case for top canopy layer: conductance from zs to hc
ic = surfvar.ntop(p);
zl = surfvar.zs(p,ic) - surfvar.hc(p);
zu = surfvar.hc(p) - surfvar.hc(p);
res = fluxvar.PrSc(p) / (fluxvar.beta(p) * fluxvar.ustar(p)) * (exp(-zl/lm_over_beta) - exp(-zu/lm_over_beta));
ga_below_hc = forcvar.rhomol(p) / res;
% Now include additional conductance from hc to first atmospheric layer
z_minus_d = surfvar.hc(p) - fluxvar.disp(p);
[psi_c_zs] = psi_c_monin_obukhov (z_minus_d / fluxvar.obu(p));
[psi_c_rsl_zs] = psi_c_rsl (z_minus_d, h_minus_d, fluxvar.obu(p), fluxvar.c1c(p), fluxvar.c2);
psic1 = -psi_c_zs + psi_c_hc + psi_c_rsl_zs - psi_c_rsl_hc;
z_minus_d = surfvar.zs(p,ic+1) - fluxvar.disp(p);
[psi_c_zs] = psi_c_monin_obukhov (z_minus_d / fluxvar.obu(p));
[psi_c_rsl_zs] = psi_c_rsl (z_minus_d, h_minus_d, fluxvar.obu(p), fluxvar.c1c(p), fluxvar.c2);
psic2 = -psi_c_zs + psi_c_hc + psi_c_rsl_zs - psi_c_rsl_hc;
psic = psic2 - psic1;
zlog = log((surfvar.zs(p,ic+1)-fluxvar.disp(p)) / (surfvar.hc(p)-fluxvar.disp(p)));
ga_above_hc = forcvar.rhomol(p) * physcon.vkc * fluxvar.ustar(p) / (zlog + psic);
fluxvar.ga_prof(p,ic) = 1 / (1 / ga_below_hc + 1 / ga_above_hc);
% Make sure above-canopy aerodynamic resistances sum to 1/gac
sumres = 1 / ga_above_hc;
for ic = surfvar.ntop(p)+1:surfvar.nlev(p)
sumres = sumres + 1 / fluxvar.ga_prof(p,ic);
end
if (abs(1/sumres - fluxvar.gac(p)) > 1e-06)
error('canopy_turbulence: above-canopy aerodynamic conductance error')
end
% Aerodynamic conductance at ground
ic = surfvar.nsoi(p);
ic_plus_one = surfvar.nsoi(p)+1;
z0m_g = 0.01; % Roughness length of ground (m)
z0c_g = 0.1 * z0m_g; % Roughness length for scalars
zlog_m = log(surfvar.zs(p,ic_plus_one)/z0m_g);
zlog_c = log(surfvar.zs(p,ic_plus_one)/z0c_g);
ustar_g = fluxvar.wind(p,ic_plus_one) * physcon.vkc / zlog_m;
ustar_g = max(ustar_g, 0.01);
res = zlog_c / (physcon.vkc * ustar_g);
fluxvar.ga_prof(p,ic) = forcvar.rhomol(p) / res;
% --- Limit resistances to < 500 s/m
for ic = surfvar.nsoi(p):surfvar.nlev(p)
res = min (forcvar.rhomol(p)/fluxvar.ga_prof(p,ic), 500);
fluxvar.ga_prof(p,ic) = forcvar.rhomol(p) / res;
end
% --- Calculate within-canopy scalar profiles for temperature and vapor pressure
[fluxvar] = scalar_profile (dt, p, physcon, forcvar, surfvar, leafvar, soilvar, fluxvar);
% --- Temperature and water vapor at top of canopy
fluxvar.taf(p) = fluxvar.tair(p,surfvar.ntop(p));
fluxvar.qaf(p) = fluxvar.qair(p,surfvar.ntop(p));
hybrid_root.m | View on GitHub
function [fluxvar, root] = hybrid_root (func, physcon, forcvar, surfvar, fluxvar, xa, xb, tol)
% Solve for the root of a function using the secant and Brent's methods given
% initial estimates xa and xb. The root is updated until its accuracy is tol.
% func is the name of the function to solve. The variable root is returned as
% the root of the function. The function being evaluated has the definition statement:
%
% function [fluxvar, fx] = func (physcon, forcvar, surfvar, fluxvar, x)
%
% The function func is exaluated at x and the returned value is fx. It uses variables
% in the physcon, forcvar, surfvar, and fluxvar structures. These are passed in as
% input arguments. It also calculates values for variables in the fluxvar structure
% so this must be returned in the function call as an output argument. The matlab
% function feval evaluates func.
% --- Evaluate func at xa and see if this is the root
x0 = xa;
[fluxvar, f0] = feval(func, physcon, forcvar, surfvar, fluxvar, x0);
if (f0 == 0)
root = x0;
return
end
% --- Evaluate func at xb and see if this is the root
x1 = xb;
[fluxvar, f1] = feval(func, physcon, forcvar, surfvar, fluxvar, x1);
if (f1 == 0)
root = x1;
return
end
% --- Order initial root estimates correctly
if (f1 < f0)
minx = x1;
minf = f1;
else
minx = x0;
minf = f0;
end
% --- Iterative root calculation. Use the secant method, with Brent's method as a backup
itmax = 40;
for iter = 1:itmax
dx = -f1 * (x1 - x0) / (f1 - f0);
x = x1 + dx;
% Check if x is the root. If so, exit the iteration
if (abs(dx) < tol)
x0 = x;
break
end
% Evaluate the function at x
x0 = x1;
f0 = f1;
x1 = x;
[fluxvar, f1] = feval(func, physcon, forcvar, surfvar, fluxvar, x1);
if (f1 < minf)
minx = x1;
minf = f1;
end
% If a root zone is found, use Brent's method for a robust backup strategy
% and exit the iteration
if (f1 * f0 < 0)
[fluxvar, x] = brent_root (func, physcon, forcvar, surfvar, fluxvar, x0, x1, tol);
x0 = x;
break
end
% In case of failing to converge within itmax iterations stop at the minimum function
if (iter == itmax)
[fluxvar, f1] = feval(func, physcon, forcvar, surfvar, fluxvar, minx);
x0 = minx;
end
end
root = x0;
obukhov_function.m | View on GitHub
function [fluxvar, fx] = obukhov_function (physcon, forcvar, surfvar, fluxvar, x)
% Use Harman & Finnigan (2007, 2008) roughness sublayer (RSL) theory to obtain
% the Obukhov length (obu). This is the function to solve for the Obukhov
% length. For the current estimate of the Obukhov length (x), calculate
% u*, T*, and q* and then the new length (obu). The function value is the
% change in Obukhov length: fx = x - obu.
% -------------------------------------------------------------------------
% Input
% x ! Current estimate for Obukhov length (m)
% physcon.vkc ! von Karman constant
% physcon.grav ! Gravitational acceleration (m/s2)
% physcon.mmh2o ! Molecular mass of water (kg/mol)
% forcvar.zref ! Reference height (m)
% forcvar.uref ! Wind speed at reference height (m/s)
% forcvar.thref ! Potential temperature at reference height (K)
% forcvar.thvref ! Virtual potential temperature at reference height (K)
% forcvar.qref ! Water vapor at reference height (mol/mol)
% forcvar.rhomol ! Molar density (mol/m3)
% forcvar.mmair ! Molecular mass of air at reference height (kg/mol)
% fluxvar.taf ! Air temperature at canopy top (K)
% fluxvar.qaf ! Water vapor at canopy top (mol/mol)
% fluxvar.Lc ! Canopy density length scale (m)
% surfvar.hc ! Canopy height (m)
% surfvar.p ! Index for grid point to process
%
% Output
% fluxvar.c1m ! Roughness sublayer c1 parameter for momentum (dimensionless)
% fluxvar.c1c ! Roughness sublayer c1 parameter for scalars (dimensionless)
% fluxvar.c2 ! Roughness sublayer depth scale multiplier (dimensionless)
% fluxvar.disp ! Displacement height (m)
% fluxvar.beta ! u* / u(hc)
% fluxvar.PrSc ! Prandtl (Schmidt) number at canopy top
% fluxvar.ustar ! Friction velocity (m/s)
% fluxvar.tstar ! Temperature scale (K)
% fluxvar.qstar ! Water vapor scale (mol/mol)
% fluxvar.gac ! Aerodynamic conductance for a scalar above canopy (mol/m2/s)
% fluxvar.obu_ustar ! Obukhov length used for u* (m)
% fluxvar.obu ! Value for Obukhov length (m)
% fx ! Change in Obukhov length (x - obu)
% -------------------------------------------------------------------------
% --- Index for grid point to process
p = surfvar.p;
% --- Prevent near-zero values of Obukhov length
if (abs(x) <= 0.1)
x = 0.1;
end
% --- Determine beta_val = u* / u(hc) for the current Obukhov length
% Neutral value for beta = u* / u(hc)
beta_neutral = 0.35;
% Lc/obu
LcL = fluxvar.Lc(p)/x;
if (LcL <= 0)
% The unstable case is a quadratic equation for beta^2 at LcL
a = 1;
b = 16 * LcL * beta_neutral^4;
c = -beta_neutral^4;
beta_val = sqrt((-b + sqrt(b^2 - 4 * a * c)) / (2 * a));
% Error check
y = beta_val^2 * LcL;
fy = (1 - 16 * y)^(-0.25);
err = beta_val * fy - beta_neutral;
if (abs(err) > 1e-10)
error('obukhov_function: unstable case - error in beta')
end
else
% The stable case is a cubic equation for beta at LcL
a = 5 * LcL;
b = 0;
c = 1;
d = -beta_neutral;
q = (2*b^3 - 9*a*b*c + 27*(a^2)*d)^2 - 4*(b^2 - 3*a*c)^3;
q = sqrt(q);
r = 0.5 * (q + 2*b^3 - 9*a*b*c + 27*(a^2)*d);
r = r^(1/3);
beta_val = -(b+r)/(3*a) - (b^2 - 3*a*c)/(3*a*r);
% Error check
y = beta_val^2 * LcL;
fy = 1 + 5 * y;
err = beta_val * fy - beta_neutral;
if (abs(err) > 1e-10)
error('obukhov_function: stable case - error in beta')
end
end
% Place limits on beta
beta_val = min(0.5, max(beta_val,0.2));
fluxvar.beta(p) = beta_val;
% --- For current beta = u*/u(hc) determine displacement height
dp = beta_val^2 * fluxvar.Lc(p); % dp = hc - disp
fluxvar.disp(p) = max(surfvar.hc(p) - dp, 0); % Displacement height (m)
% Save reference height and canopy height (relative to displacement height)
% because these are used many times
z_minus_d = forcvar.zref(p) - fluxvar.disp(p);
h_minus_d = surfvar.hc(p) - fluxvar.disp(p);
% --- Turbulent Prandlt (Schmidt) number (PrSc) at canopy height
PrSc0 = 0.5; % Neutral value for Pr (Sc)
PrSc1 = 0.3; % Magnitude of variation of Pr (Sc) with stability
PrSc2 = 2.0; % Scale of variation of Pr (Sc) with stability
fluxvar.PrSc(p) = PrSc0 + PrSc1 * tanh(PrSc2*fluxvar.Lc(p)/x);
% --- Calculate the parameters c1 and c2 needed for the RSL function phi_hat
% Evaluate Monin-Obukhov phi functions at (hc-disp)/obu
[phi_m_hc] = phi_m_monin_obukhov (h_minus_d / x);
[phi_c_hc] = phi_c_monin_obukhov (h_minus_d / x);
% Roughness sublayer depth scale multiplier (dimensionless)
fluxvar.c2 = 0.5;
% c1 for momentum and scalars (dimensionless)
fluxvar.c1m(p) = (1 - physcon.vkc / (2 * beta_val * phi_m_hc)) * exp(fluxvar.c2/2);
fluxvar.c1c(p) = (1 - fluxvar.PrSc(p)*physcon.vkc / (2 * beta_val * phi_c_hc)) * exp(fluxvar.c2/2);
% --- Evaluate the roughness sublayer psi_hat functions for momentum and scalars
% These are calculated at the reference height and at the canopy height. Note that
% here the heights are adjusted for the displacement height before the integration.
[psi_m_rsl_zref] = psi_m_rsl (z_minus_d, h_minus_d, x, fluxvar.c1m(p), fluxvar.c2); % momentum at (zref-disp)
[psi_m_rsl_hc] = psi_m_rsl (h_minus_d, h_minus_d, x, fluxvar.c1m(p), fluxvar.c2); % momentum at (hc-disp)
[psi_c_rsl_zref] = psi_c_rsl (z_minus_d, h_minus_d, x, fluxvar.c1c(p), fluxvar.c2); % scalars at (zref-disp)
[psi_c_rsl_hc] = psi_c_rsl (h_minus_d, h_minus_d, x, fluxvar.c1c(p), fluxvar.c2); % scalars at (hc-disp)
% --- Evaluate the Monin-Obukhov psi functions for momentum and scalars
% These are calculated at the reference height and at the canopy height
[psi_m_zref] = psi_m_monin_obukhov (z_minus_d / x); % momentum at (zref-disp)/obu
[psi_m_hc] = psi_m_monin_obukhov (h_minus_d / x); % momentum at (hc-disp)/obu
[psi_c_zref] = psi_c_monin_obukhov (z_minus_d / x); % scalars at (zref-disp)/obu
[psi_c_hc] = psi_c_monin_obukhov (h_minus_d / x); % scalars at (hc-disp)/obu
% --- Calculate u* (m/s), T* (K), q* (mol/mol), and Tv* (K)
zlog = log(z_minus_d / h_minus_d);
psim = -psi_m_zref + psi_m_hc + psi_m_rsl_zref - psi_m_rsl_hc + physcon.vkc / beta_val;
psic = -psi_c_zref + psi_c_hc + psi_c_rsl_zref - psi_c_rsl_hc;
fluxvar.ustar(p) = forcvar.uref(p) * physcon.vkc / (zlog + psim);
fluxvar.tstar(p) = (forcvar.thref(p) - fluxvar.taf(p)) * physcon.vkc / (zlog + psic);
fluxvar.qstar(p) = (forcvar.qref(p) - fluxvar.qaf(p)) * physcon.vkc / (zlog + psic);
fluxvar.obu_ustar(p) = x;
% --- Aerodynamic conductance to canopy height
fluxvar.gac(p) = forcvar.rhomol(p) * physcon.vkc * fluxvar.ustar(p) / (zlog + psic);
% --- Calculate new Obukhov length (m)
tvstar = fluxvar.tstar(p) + 0.61 * forcvar.thref(p) * fluxvar.qstar(p) * (physcon.mmh2o / forcvar.mmair(p));
fluxvar.obu(p) = fluxvar.ustar(p)^2 * forcvar.thvref(p) / (physcon.vkc * physcon.grav * tvstar);
fx = x - fluxvar.obu(p);
phi_c_monin_obukhov.m | View on GitHub
function [phi_c] = phi_c_monin_obukhov (x)
% --- Evaluate the Monin-Obukhov phi function for scalars at x
if (x < 0)
phi_c = (1 - 16 * x)^(-0.5);
else
phi_c = 1 + 5 * x;
end
phi_m_monin_obukhov.m | View on GitHub
function [phi_m] = phi_m_monin_obukhov (x)
% --- Evaluate the Monin-Obukhov phi function for momentum at x
if (x < 0)
phi_m = (1 - 16 * x)^(-0.25);
else
phi_m = 1 + 5 * x;
end
psi_c_monin_obukhov.m | View on GitHub
function [psi_c] = psi_c_monin_obukhov (x)
% --- Evaluate the Monin-Obukhov psi function for scalars at x
if (x < 0)
y = (1 - 16 * x)^0.25;
psi_c = 2 * log((1 + y^2)/2);
else
psi_c = -5 * x;
end
psi_c_rsl.m | View on GitHub
function [psi_hat_c] = psi_c_rsl (z, h, L, c1, c2)
% --- Evaluate the roughness sublayer (RSL) function psi_hat for scalars
% at z. Note that z has already been adjusted for the displacement height
% (i.e., using z - d).
% ------------------------------------------------------
% Input
% z ! Vertical height - displacement height (m)
% h ! Canopy height - displacement height (m)
% L ! Obukhov length (m)
% c1 ! Parameter for RSL function phi_hat (dimensionless)
% c2 ! Parameter for RSL function phi_hat (dimensionless)
%
% Output
% psi_hat_c ! RSL psi_hat function for scalars (dimensionless)
% ------------------------------------------------------
% The function to integrate depends on unstable (f1) or stable (f2)
f1 = @(x) (1-16*x/L).^(-0.5) .* (1 - (1 - c1*exp(-c2*x/(2*h)))) ./ x;
f2 = @(x) (1+5*x/L) .* (1 - (1 - c1*exp(-c2*x/(2*h)))) ./ x;
% Numerically integrate the function from z to infinity
if (L < 0)
psi_hat_c = integral (f1, z, inf);
else
psi_hat_c = integral (f2, z, inf);
end
psi_m_monin_obukhov.m | View on GitHub
function [psi_m] = psi_m_monin_obukhov (x)
% --- Evaluate the Monin-Obukhov psi function for momentum at x
if (x < 0)
y = (1 - 16 * x)^0.25;
psi_m = 2 * log((1 + y)/2) + log((1 + y^2)/2) - 2 * atan(y) + pi / 2;
else
psi_m = -5 * x;
end
psi_m_rsl.m | View on GitHub
function [psi_hat_m] = psi_m_rsl (z, h, L, c1, c2)
% --- Evaluate the roughness sublayer (RSL) function psi_hat for momentum
% at z. Note that z has already been adjusted for the displacement height
% (i.e., using z - d).
% ------------------------------------------------------
% Input
% z ! Vertical height - displacement height (m)
% h ! Canopy height - displacement height (m)
% L ! Obukhov length (m)
% c1 ! Parameter for RSL function phi_hat (dimensionless)
% c2 ! Parameter for RSL function phi_hat (dimensionless)
%
% Output
% psi_hat_m ! RSL psi_hat function for momentum (dimensionless)
% ------------------------------------------------------
% The function to integrate depends on unstable (f1) or stable (f2)
f1 = @(x) (1-16*x/L).^(-0.25) .* (1 - (1 - c1*exp(-c2*x/(2*h)))) ./ x;
f2 = @(x) (1+5*x/L) .* (1 - (1 - c1*exp(-c2*x/(2*h)))) ./ x;
% Numerically integrate the function from z to infinity
if (L < 0)
psi_hat_m = integral (f1, z, inf);
else
psi_hat_m = integral (f2, z, inf);
end
satvap.m | View on GitHub
function [esat, desat] = satvap (tc)
% Compute saturation vapor pressure and change in saturation vapor pressure
% with respect to temperature. Polynomial approximations are from:
% Flatau et al. (1992) Polynomial fits to saturation vapor pressure.
% Journal of Applied Meteorology 31:1507-1513. Input temperature is Celsius.
% --- For water vapor (temperature range is 0C to 100C)
a0 = 6.11213476; b0 = 0.444017302;
a1 = 0.444007856; b1 = 0.286064092e-01;
a2 = 0.143064234e-01; b2 = 0.794683137e-03;
a3 = 0.264461437e-03; b3 = 0.121211669e-04;
a4 = 0.305903558e-05; b4 = 0.103354611e-06;
a5 = 0.196237241e-07; b5 = 0.404125005e-09;
a6 = 0.892344772e-10; b6 = -0.788037859e-12;
a7 = -0.373208410e-12; b7 = -0.114596802e-13;
a8 = 0.209339997e-15; b8 = 0.381294516e-16;
% --- For ice (temperature range is -75C to 0C)
c0 = 6.11123516; d0 = 0.503277922;
c1 = 0.503109514; d1 = 0.377289173e-01;
c2 = 0.188369801e-01; d2 = 0.126801703e-02;
c3 = 0.420547422e-03; d3 = 0.249468427e-04;
c4 = 0.614396778e-05; d4 = 0.313703411e-06;
c5 = 0.602780717e-07; d5 = 0.257180651e-08;
c6 = 0.387940929e-09; d6 = 0.133268878e-10;
c7 = 0.149436277e-11; d7 = 0.394116744e-13;
c8 = 0.262655803e-14; d8 = 0.498070196e-16;
% --- Limit temperature to -75C to 100C
tc = min(tc, 100);
tc = max(tc, -75);
% --- Saturation vapor pressure (esat, mb) and derivative (desat, mb)
if (tc >= 0)
esat = a0 + tc*(a1 + tc*(a2 + tc*(a3 + tc*(a4 ...
+ tc*(a5 + tc*(a6 + tc*(a7 + tc*a8)))))));
desat = b0 + tc*(b1 + tc*(b2 + tc*(b3 + tc*(b4 ...
+ tc*(b5 + tc*(b6 + tc*(b7 + tc*b8)))))));
else
esat = c0 + tc*(c1 + tc*(c2 + tc*(c3 + tc*(c4 ...
+ tc*(c5 + tc*(c6 + tc*(c7 + tc*c8)))))));
desat = d0 + tc*(d1 + tc*(d2 + tc*(d3 + tc*(d4 ...
+ tc*(d5 + tc*(d6 + tc*(d7 + tc*d8)))))));
end
% --- Convert from mb to Pa
esat = esat * 100;
desat = desat * 100;
scalar_profile.m | View on GitHub
function [fluxvar] = scalar_profile (dt, p, physcon, forcvar, surfvar, leafvar, soilvar, fluxvar)
% Compute scalar profiles for temperature and water vapor using an implicit
% solution. The boundary condition is the above-canopy scalar values at the
% reference height. The vegetation and ground temperature and fluxes are
% calculated as part of the implicit solution.
% -----------------------------------------------------------------------------------
% Input
% dt ! Model time step (s)
% p ! Index for grid point to process
% physcon.tfrz ! Freezing point of water (K)
% physcon.hvap ! Latent heat of evaporation (J/kg)
% physcon.mmh2o ! Molecular mass of water (kg/mol)
% forcvar.rhomol ! Molar density (mol/m3)
% forcvar.cpair ! Specific heat of air at constant pressure (J/mol/K)
% forcvar.pref ! Atmospheric pressure (Pa)
% forcvar.thref ! Potential temperature at reference height (K)
% forcvar.qref ! Water vapor at reference height (mol/mol)
% surfvar.nlev ! Index for top level
% surfvar.ntop ! Index for top leaf layer
% surfvar.nsoi ! First canopy layer is soil
% surfvar.zw ! Canopy height at layer interfaces (m)
% surfvar.dpai ! Layer plant area index (m2/m2)
% surfvar.fwet ! Fraction of plant area index that is wet
% surfvar.fdry ! Fraction of plant area index that is green and dry
% surfvar.fracsun ! Sunlit fraction of canopy layer
% surfvar.fracsha ! Shaded fraction of canopy layer
% leafvar.nleaf ! Number of leaf types (sunlit and shaded)
% leafvar.isun ! Sunlit leaf index
% leafvar.isha ! Shaded leaf index
% leafvar.gbh ! Leaf boundary layer conductance, heat (mol/m2 leaf/s)
% leafvar.gbv ! Leaf boundary layer conductance, H2O (mol H2O/m2 leaf/s)
% leafvar.gs ! Leaf stomatal conductance (mol H2O/m2 leaf/s)
% leafvar.cpleaf ! Leaf heat capacity (J/m2 leaf/K)
% leafvar.rnleaf ! Leaf net radiation (W/m2 leaf)
% soilvar.tk ! Soil thermal conductivity (W/m/K)
% soilvar.dz ! Soil layer depth (m)
% soilvar.tsoi ! Soil temperature (K)
% soilvar.resis ! Soil evaporative resistance (s/m)
% soilvar.rhg ! Relative humidity of airspace at soil surface (fraction)
% fluxvar.rnsoi ! Net radiation at ground (W/m2)
% fluxvar.tair_old ! Air temperature profile for previous timestep (K)
% fluxvar.qair_old ! Water vapor profile for previous timestep (mol/mol)
% fluxvar.tveg_old ! Vegetation temperature profile for previous timestep (K)
% fluxvar.ga_prof ! Canopy layer aerodynamic conductance for scalars (mol/m2/s)
% Output
% fluxvar.tair ! Air temperature profile (K)
% fluxvar.qair ! Water vapor profile (mol/mol)
% fluxvar.tveg ! Vegetation temperature profile (K)
% fluxvar.shsoi ! Ground sensible heat flux, ground (W/m2)
% fluxvar.etsoi ! Ground evaporation flux (mol H2O/m2/s)
% fluxvar.gsoi ! Soil heat flux (W/m2)
% fluxvar.tg ! Soil surface temperature (K)
% fluxvar.shveg ! Leaf sensible heat flux (W/m2 leaf)
% fluxvar.etveg ! Leaf evapotranspiration flux (mol H2O/m2 leaf/s)
% fluxvar.stveg ! Leaf storage heat flux (W/m2 leaf)
% fluxvar.shair ! Canopy air sensible heat flux (W/m2)
% fluxvar.etair ! Canopy air water vapor flux (mol H2O/m2/s)
% fluxvar.stair ! Canopy air storage heat flux (W/m2)
% -----------------------------------------------------------------------------------
% Latent heat of vaporization (J/mol)
lambda = physcon.hvap * physcon.mmh2o;
% --------------------------------------------------------------------------
% Terms for ground temperature, which is calculated from the energy balance:
% Rn0 - H0 - lambda*E0 - G = 0
% and is rewritten as:
% T0 = alpha0*T(1) + beta0*q(1) + delta0
% --------------------------------------------------------------------------
% array index for ground
ic = surfvar.nsoi(p);
% Saturation vapor pressure and derivative at ground temperature
[esat, desat] = satvap (fluxvar.tair_old(p,ic)-physcon.tfrz); % Pa
qsat0 = esat / forcvar.pref(p); % Pa -> mol/mol
dqsat0 = desat / forcvar.pref(p); % Pa -> mol/mol
% Total soil-to-air conductance for water vapor (mol H2O/m2/s)
gsw = (1 / soilvar.resis(p)) * forcvar.rhomol(p); % soil: s/m -> mol H2O/m2/s
gsa = fluxvar.ga_prof(p,ic); % aerodynamic
gs0 = gsa * gsw / (gsa + gsw); % total conductance
% Terms for soil heat flux
c02 = soilvar.tk(p) / soilvar.dz(p);
c01 = -c02 * soilvar.tsoi(p);
% Coefficients for ground temperature
den = forcvar.cpair(p) * fluxvar.ga_prof(p,ic) + lambda * soilvar.rhg(p) * gs0 * dqsat0 + c02;
alpha0 = forcvar.cpair(p) * fluxvar.ga_prof(p,ic) / den;
beta0 = lambda * gs0 / den;
delta0 = (fluxvar.rnsoi(p) - lambda * soilvar.rhg(p) * gs0 * (qsat0 - dqsat0 * fluxvar.tair_old(p,ic)) - c01) / den;
% ---------------------------------------------------------------------
% alpha, beta, delta coefficients for leaf temperature:
%
% Tlsun(i) = alpha_sun(i)*T(i) + beta_sun(i)*q(i) + delta_sun(i)
% Tlsha(i) = alpha_sha(i)*T(i) + beta_sha(i)*q(i) + delta_sha(i)
%
% and leaf terms needed for scalar conservations equations. These
% are defined for all layers but the leaf terms only exist for
% the layers with leaves.
% ---------------------------------------------------------------------
for ic = surfvar.nsoi(p)+1:surfvar.nlev(p)
if (surfvar.dpai(p,ic) > 0)
% Calculate terms for sunlit and shaded leaves
for il = 1:leafvar.nleaf
% Leaf conductances (here these are per unit leaf area)
gleaf_sh(ic,il) = 2 * leafvar.gbh(p,ic,il);
gleaf = leafvar.gs(p,ic,il) * leafvar.gbv(p,ic,il) / (leafvar.gs(p,ic,il) + leafvar.gbv(p,ic,il));
gleaf_et(ic,il) = gleaf * surfvar.fdry(p,ic) + leafvar.gbv(p,ic,il) * surfvar.fwet(p,ic);
% Heat capacity of leaves
heatcap(ic,il) = leafvar.cpleaf(p,ic);
% Available energy: net radiation
avail_energy(ic,il) = leafvar.rnleaf(p,ic,il);
% Saturation vapor pressure and derivative for leaf temperature at time n: Pa -> mol/mol
[esat, desat] = satvap (fluxvar.tveg_old(p,ic,il)-physcon.tfrz);
qsat(ic,il) = esat / forcvar.pref(p);
dqsat(ic,il) = desat / forcvar.pref(p);
% Term for linearized vapor pressure at leaf temperature:
% qsat(tveg) = qsat(tveg_old) + dqsat * (tveg - tveg_old)
% Here qsat_term contains the terms with tveg_old
qsat_term(ic,il) = qsat(ic,il) - dqsat(ic,il) * fluxvar.tveg_old(p,ic,il);
% alpha, beta, delta coefficients for leaf temperature
den = heatcap(ic,il) / dt + gleaf_sh(ic,il) * forcvar.cpair(p) + gleaf_et(ic,il) * lambda * dqsat(ic,il);
alpha(ic,il) = gleaf_sh(ic,il) * forcvar.cpair(p) / den;
beta(ic,il) = gleaf_et(ic,il) * lambda / den;
delta(ic,il) = avail_energy(ic,il) / den ...
- lambda * gleaf_et(ic,il) * qsat_term(ic,il) / den ...
+ heatcap(ic,il) / dt * fluxvar.tveg_old(p,ic,il) / den;
% Now scale flux terms for plant area
if (il == leafvar.isun)
pai = surfvar.fracsun(p,ic) * surfvar.dpai(p,ic);
elseif (il == leafvar.isha)
pai = surfvar.fracsha(p,ic) * surfvar.dpai(p,ic);
end
gleaf_sh(ic,il) = gleaf_sh(ic,il) * pai;
gleaf_et(ic,il) = gleaf_et(ic,il) * pai;
heatcap(ic,il) = heatcap(ic,il) * pai;
avail_energy(ic,il) = avail_energy(ic,il) * pai;
end
else
% Zero out terms
for il = 1:leafvar.nleaf
gleaf_sh(ic,il) = 0;
gleaf_et(ic,il) = 0;
heatcap(ic,il) = 0;
avail_energy(ic,il) = 0;
qsat(ic,il) = 0;
dqsat(ic,il) = 0;
qsat_term(ic,il) = 0;
alpha(ic,il) = 0;
beta(ic,il) = 0;
delta(ic,il) = 0;
end
end
end
% ---------------------------------------------------------------------
% a,b,c,d coefficients for air temperature:
% a1(i)*T(i-1) + b11(i)*T(i) + b12(i)*q(i) + c1(i)*T(i+1) = d1(i)
%
% a,b,c,d coefficients for water vapor (mole fraction):
% a2(i)*q(i-1) + b21(i)*T(i) + b22(i)*q(i) + c2(i)*q(i+1) = d2(i)
% ---------------------------------------------------------------------
for ic = surfvar.nsoi(p)+1:surfvar.nlev(p)
% Storage term
rho_dz_over_dt = forcvar.rhomol(p) * (surfvar.zw(p,ic) - surfvar.zw(p,ic-1)) / dt;
% a1,b11,b12,c1,d1 coefficients for air temperature
a1(ic) = -fluxvar.ga_prof(p,ic-1);
b11(ic) = rho_dz_over_dt + fluxvar.ga_prof(p,ic-1) + fluxvar.ga_prof(p,ic) ...
+ gleaf_sh(ic,leafvar.isun) * (1 - alpha(ic,leafvar.isun)) ...
+ gleaf_sh(ic,leafvar.isha) * (1 - alpha(ic,leafvar.isha));
b12(ic) = -gleaf_sh(ic,leafvar.isun) * beta(ic,leafvar.isun) - gleaf_sh(ic,leafvar.isha) * beta(ic,leafvar.isha);
c1(ic) = -fluxvar.ga_prof(p,ic);
d1(ic) = rho_dz_over_dt * fluxvar.tair_old(p,ic) + gleaf_sh(ic,leafvar.isun) * delta(ic,leafvar.isun) ...
+ gleaf_sh(ic,leafvar.isha) * delta(ic,leafvar.isha);
% Special case for top layer
if (ic == surfvar.nlev(p))
c1(ic) = 0;
d1(ic) = d1(ic) + fluxvar.ga_prof(p,ic) * forcvar.thref(p);
end
% Special case for first canopy layer (i.e., immediately above the ground)
if (ic == surfvar.nsoi(p)+1)
a1(ic) = 0;
b11(ic) = b11(ic) - fluxvar.ga_prof(p,surfvar.nsoi(p)) * alpha0;
b12(ic) = b12(ic) - fluxvar.ga_prof(p,surfvar.nsoi(p)) * beta0;
d1(ic) = d1(ic) + fluxvar.ga_prof(p,surfvar.nsoi(p)) * delta0;
end
% a2,b21,b22,c2,d2 coefficients for water vapor (mole fraction)
if (ic == surfvar.nsoi(p)+1)
ga_prof_ic_minus_one = gs0;
else
ga_prof_ic_minus_one = fluxvar.ga_prof(p,ic-1);
end
a2(ic) = -ga_prof_ic_minus_one;
b21(ic) = -gleaf_et(ic,leafvar.isun) * dqsat(ic,leafvar.isun) * alpha(ic,leafvar.isun) ...
-gleaf_et(ic,leafvar.isha) * dqsat(ic,leafvar.isha) * alpha(ic,leafvar.isha);
b22(ic) = rho_dz_over_dt + ga_prof_ic_minus_one + fluxvar.ga_prof(p,ic) ...
+ gleaf_et(ic,leafvar.isun) * (1 - dqsat(ic,leafvar.isun) * beta(ic,leafvar.isun)) ...
+ gleaf_et(ic,leafvar.isha) * (1 - dqsat(ic,leafvar.isha) * beta(ic,leafvar.isha));
c2(ic) = -fluxvar.ga_prof(p,ic);
d2(ic) = rho_dz_over_dt * fluxvar.qair_old(p,ic) ...
+ gleaf_et(ic,leafvar.isun) * (dqsat(ic,leafvar.isun) * delta(ic,leafvar.isun) + qsat_term(ic,leafvar.isun)) ...
+ gleaf_et(ic,leafvar.isha) * (dqsat(ic,leafvar.isha) * delta(ic,leafvar.isha) + qsat_term(ic,leafvar.isha));
% Special case for top layer
if (ic == surfvar.nlev(p))
c2(ic) = 0;
d2(ic) = d2(ic) + fluxvar.ga_prof(p,ic) * forcvar.qref(p);
end
% Special case for first canopy layer (i.e., immediately above the ground)
if (ic == surfvar.nsoi(p)+1)
a2(ic) = 0;
b21(ic) = b21(ic) - gs0 * soilvar.rhg(p) * dqsat0 * alpha0;
b22(ic) = b22(ic) - gs0 * soilvar.rhg(p) * dqsat0 * beta0;
d2(ic) = d2(ic) + gs0 * soilvar.rhg(p) * (qsat0 + dqsat0 * (delta0 - fluxvar.tair_old(p,surfvar.nsoi(p))));
end
end
% ---------------------------------------------------------------------
% Solve for air temperature and water vapor (mole fraction):
%
% a1(i)*T(i-1) + b11(i)*T(i) + b12(i)*q(i) + c1(i)*T(i+1) = d1(i)
% a2(i)*q(i-1) + b21(i)*T(i) + b22(i)*q(i) + c2(i)*q(i+1) = d2(i)
%
% The solution rewrites these equations so that:
% T(i) = f1(i) - e11(i)*T(i+1) - e12(i)*q(i+1)
% q(i) = f2(i) - e21(i)*T(i+1) - e22(i)*q(i+1)
% ---------------------------------------------------------------------
ic = surfvar.nsoi(p);
e11(ic) = 0;
e12(ic) = 0;
e21(ic) = 0;
e22(ic) = 0;
f1(ic) = 0;
f2(ic) = 0;
for ic = surfvar.nsoi(p)+1:surfvar.nlev(p)
% The matrix to invert is:
%
% B(i)- A(i)*E(i-1)
%
% which is a 2x2 matrix. The
% elements in the 2x2 matrix are:
%
% | a b |
% B(i)- A(i)*E(i-1) = | c d |
%
% Calculate these elements (denoted by ainv,binv,
% cinv,dinv) and the determinant of the matrix.
ainv = b11(ic) - a1(ic) * e11(ic-1);
binv = b12(ic) - a1(ic) * e12(ic-1);
cinv = b21(ic) - a2(ic) * e21(ic-1);
dinv = b22(ic) - a2(ic) * e22(ic-1);
det = ainv * dinv - binv * cinv;
% E(i) = [B(i) - A(i)*E(i-1)]^(-1) * C(i)
e11(ic) = dinv * c1(ic) / det;
e12(ic) = -binv * c2(ic) / det;
e21(ic) = -cinv * c1(ic) / det;
e22(ic) = ainv * c2(ic) / det;
% F(i) = [B(i) - A(i)*E(i-1)]^(-1) * [D(i) - A(i)*F(i-1)]
f1(ic) = (dinv*(d1(ic) - a1(ic)*f1(ic-1)) - binv*(d2(ic) - a2(ic)*f2(ic-1))) / det;
f2(ic) = (-cinv*(d1(ic) - a1(ic)*f1(ic-1)) + ainv*(d2(ic) - a2(ic)*f2(ic-1))) / det;
end
% Top layer
ic = surfvar.nlev(p);
fluxvar.tair(p,ic) = f1(ic);
fluxvar.qair(p,ic) = f2(ic);
% Layers through to bottom of canopy
for ic = surfvar.nlev(p)-1: -1: surfvar.nsoi(p)+1
fluxvar.tair(p,ic) = f1(ic) - e11(ic)*fluxvar.tair(p,ic+1) - e12(ic)*fluxvar.qair(p,ic+1);
fluxvar.qair(p,ic) = f2(ic) - e21(ic)*fluxvar.tair(p,ic+1) - e22(ic)*fluxvar.qair(p,ic+1);
end
% Ground
ic = surfvar.nsoi(p);
fluxvar.tg(p) = alpha0 * fluxvar.tair(p,ic+1) + beta0 * fluxvar.qair(p,ic+1) + delta0;
fluxvar.tair(p,ic) = fluxvar.tg(p);
fluxvar.qair(p,ic) = soilvar.rhg(p) * (qsat0 + dqsat0 * (fluxvar.tair(p,ic) - fluxvar.tair_old(p,ic)));
% ---------------------------------------------------------------------
% Calculate leaf temperature:
% Tlsun(i) = alpha_sun(i)*T(i) + beta_sun(i)*q(i) + delta_sun(i)
% Tlsha(i) = alpha_sha(i)*T(i) + beta_sha(i)*q(i) + delta_sha(i)
% ---------------------------------------------------------------------
for ic = surfvar.nsoi(p)+1:surfvar.nlev(p)
fluxvar.tveg(p,ic,leafvar.isun) = alpha(ic,leafvar.isun)*fluxvar.tair(p,ic) ...
+ beta(ic,leafvar.isun)*fluxvar.qair(p,ic) + delta(ic,leafvar.isun);
fluxvar.tveg(p,ic,leafvar.isha) = alpha(ic,leafvar.isha)*fluxvar.tair(p,ic) ...
+ beta(ic,leafvar.isha)*fluxvar.qair(p,ic) + delta(ic,leafvar.isha);
% Special checks for no plant area in layer
if (surfvar.dpai(p,ic) > 0)
pai = surfvar.fracsun(p,ic) * surfvar.dpai(p,ic);
if (pai == 0)
fluxvar.tveg(p,ic,leafvar.isun) = fluxvar.tair(p,ic);
end
pai = surfvar.fracsha(p,ic) * surfvar.dpai(p,ic);
if (pai == 0)
fluxvar.tveg(p,ic,leafvar.isha) = fluxvar.tair(p,ic);
end
else
fluxvar.tveg(p,ic,leafvar.isun) = 0;
fluxvar.tveg(p,ic,leafvar.isha) = 0;
end
end
ic = surfvar.nsoi(p);
fluxvar.tveg(p,ic,leafvar.isun) = 0;
fluxvar.tveg(p,ic,leafvar.isha) = 0;
% --------------------
% Ground source fluxes
% --------------------
ic = surfvar.nsoi(p);
fluxvar.shsoi(p) = -forcvar.cpair(p) * (fluxvar.tair(p,ic+1) - fluxvar.tair(p,ic)) * fluxvar.ga_prof(p,ic);
fluxvar.etsoi(p) = -(fluxvar.qair(p,ic+1) - fluxvar.qair(p,ic)) * gs0;
fluxvar.gsoi(p) = c01 + c02 * fluxvar.tg(p);
% ------------------------
% Vegetation source fluxes
% ------------------------
for ic = surfvar.nsoi(p)+1:surfvar.nlev(p)
fluxvar.shveg(p,ic) = 0;
fluxvar.etveg(p,ic) = 0;
fluxvar.stveg(p,ic) = 0;
for il = 1:leafvar.nleaf
fluxvar.shveg(p,ic) = fluxvar.shveg(p,ic) ...
+ forcvar.cpair(p) * (fluxvar.tveg(p,ic,il) - fluxvar.tair(p,ic)) * gleaf_sh(ic,il);
fluxvar.etveg(p,ic) = fluxvar.etveg(p,ic) ...
+ (qsat(ic,il) + dqsat(ic,il) * (fluxvar.tveg(p,ic,il) - fluxvar.tveg_old(p,ic,il)) - fluxvar.qair(p,ic)) ...
* gleaf_et(ic,il);
fluxvar.stveg(p,ic) = fluxvar.stveg(p,ic) ...
+ heatcap(ic,il) * (fluxvar.tveg(p,ic,il) - fluxvar.tveg_old(p,ic,il)) / dt;
end
end
% ------------------------------------------------------------
% Vertical sensible heat and water vapor fluxes between layers
% ------------------------------------------------------------
for ic = surfvar.nsoi(p)+1:surfvar.nlev(p)-1
fluxvar.shair(p,ic) = -forcvar.cpair(p) * (fluxvar.tair(p,ic+1) - fluxvar.tair(p,ic)) * fluxvar.ga_prof(p,ic);
fluxvar.etair(p,ic) = -(fluxvar.qair(p,ic+1) - fluxvar.qair(p,ic)) * fluxvar.ga_prof(p,ic);
end
ic = surfvar.nlev(p);
fluxvar.shair(p,ic) = -forcvar.cpair(p) * (forcvar.thref(p) - fluxvar.tair(p,ic)) * fluxvar.ga_prof(p,ic);
fluxvar.etair(p,ic) = -(forcvar.qref(p) - fluxvar.qair(p,ic)) * fluxvar.ga_prof(p,ic);
% --------------------------------------------------------------------------
% Canopy air storage flux (W/m2) and its sensible heat and water vapor terms
% --------------------------------------------------------------------------
for ic = surfvar.nsoi(p)+1:surfvar.nlev(p)
dz_over_dt = (surfvar.zw(p,ic) - surfvar.zw(p,ic-1)) / dt;
storage_sh(ic) = forcvar.rhomol(p) * forcvar.cpair(p) * (fluxvar.tair(p,ic) - fluxvar.tair_old(p,ic)) * dz_over_dt;
storage_et(ic) = forcvar.rhomol(p) * (fluxvar.qair(p,ic) - fluxvar.qair_old(p,ic)) * dz_over_dt;
fluxvar.stair(p,ic) = storage_sh(ic) + storage_et(ic) * lambda;
end
% -------------------
% Conservation checks
% -------------------
% Ground source fluxes energy balance
err = fluxvar.rnsoi(p) - fluxvar.shsoi(p) - lambda * fluxvar.etsoi(p) - fluxvar.gsoi(p);
if (abs(err) > 0.001)
error ('ScalarProfile: Ground temperature energy balance error')
end
% Vegetation source fluxes energy balance
for ic = surfvar.nsoi(p)+1:surfvar.nlev(p)
err = avail_energy(ic,leafvar.isun) + avail_energy(ic,leafvar.isha) ...
- fluxvar.shveg(p,ic) - lambda * fluxvar.etveg(p,ic) - fluxvar.stveg(p,ic);
if (abs(err) > 0.001)
error ('ScalarProfile: Leaf temperature energy balance error')
end
end
% Flux conservation at each layer. Note special case for first canopy layer.
for ic = surfvar.nsoi(p)+1:surfvar.nlev(p)
if (ic == surfvar.nsoi(p)+1)
err = storage_sh(ic) - (fluxvar.shsoi(p) + fluxvar.shveg(p,ic) - fluxvar.shair(p,ic));
else
err = storage_sh(ic) - (fluxvar.shair(p,ic-1) + fluxvar.shveg(p,ic) - fluxvar.shair(p,ic));
end
if (abs(err) > 0.001)
error ('ScalarProfile: Sensible heat layer conservation error')
end
if (ic == surfvar.nsoi(p)+1)
err = storage_et(ic) - (fluxvar.etsoi(p) + fluxvar.etveg(p,ic) - fluxvar.etair(p,ic));
else
err = storage_et(ic) - (fluxvar.etair(p,ic-1) + fluxvar.etveg(p,ic) - fluxvar.etair(p,ic));
end
err = err * lambda;
if (abs(err) > 0.001)
err ('ScalarProfile: Latent heat layer conservation error')
end
end
% Flux conservation for canopy sensible heat. This is to check canopy
% conservation equation (so the sum is to ntop not nlev).
sum_src = fluxvar.shsoi(p);
sum_storage = 0;
for ic = surfvar.nsoi(p)+1:surfvar.ntop(p)
sum_src = sum_src + fluxvar.shveg(p,ic);
sum_storage = sum_storage + storage_sh(ic);
end
err = (sum_src - sum_storage) - fluxvar.shair(p,surfvar.ntop(p));
if (abs(err) > 0.001)
error ('ScalarProfile: Sensible heat canopy conservation error')
end
% Flux conservation for canopy latent heat. This is to check canopy
% conservation equation (so the sum is to ntop not nlev).
sum_src = fluxvar.etsoi(p);
sum_storage = 0;
for ic = surfvar.nsoi(p)+1:surfvar.ntop(p)
sum_src = sum_src + fluxvar.etveg(p,ic);
sum_storage = sum_storage + storage_et(ic);
end
err = (sum_src - sum_storage) - fluxvar.etair(p,surfvar.ntop(p));
err = err * lambda;
if (abs(err) > 0.001)
error ('ScalarProfile: Latent heat canopy conservation error')
end
Output
Figures
Figure 1
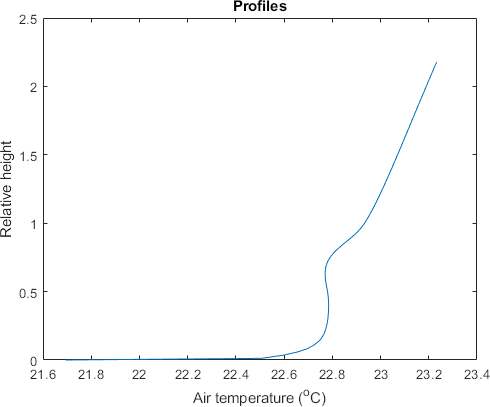
Text
sp_16_01_out.txt (standard output) | View on GitHub | View raw
0 0.000 0.000 0.000 294.843 2586.238 0.000 0.000
1 0.250 0.000 0.100 295.656 1542.385 0.000 0.000
2 0.750 0.000 0.100 295.748 1527.280 0.000 0.000
3 1.250 0.000 0.100 295.807 1517.844 0.000 0.000
4 1.750 0.000 0.100 295.846 1511.950 0.000 0.000
5 2.250 0.000 0.100 295.872 1508.345 0.000 0.000
6 2.750 0.010 0.100 295.890 1506.272 296.542 295.895
7 3.250 0.015 0.100 295.903 1505.245 296.552 295.906
8 3.750 0.021 0.100 295.912 1504.967 296.558 295.914
9 4.250 0.028 0.100 295.918 1505.246 296.562 295.919
10 4.750 0.036 0.100 295.923 1505.951 296.565 295.924
11 5.250 0.045 0.100 295.926 1506.991 296.566 295.927
12 5.750 0.054 0.100 295.929 1508.302 296.566 295.930
13 6.250 0.064 0.100 295.931 1509.832 296.565 295.932
14 6.750 0.075 0.100 295.933 1511.540 296.563 295.934
15 7.250 0.087 0.100 295.934 1513.393 296.560 295.935
16 7.750 0.099 0.100 295.934 1515.360 296.558 295.937
17 8.250 0.112 0.100 295.935 1517.414 296.548 295.937
18 8.750 0.124 0.100 295.934 1519.531 296.544 295.938
19 9.250 0.137 0.100 295.934 1521.689 296.539 295.938
20 9.750 0.149 0.100 295.933 1523.867 296.532 295.938
21 10.250 0.162 0.100 295.931 1526.047 296.521 295.937
22 10.750 0.174 0.114 295.929 1528.211 296.509 295.937
23 11.250 0.185 0.130 295.926 1530.345 296.501 295.924
24 11.750 0.196 0.148 295.924 1532.368 296.487 295.922
25 12.250 0.206 0.169 295.922 1534.274 296.474 295.909
26 12.750 0.214 0.192 295.921 1536.000 296.462 295.909
27 13.250 0.222 0.219 295.920 1537.556 296.449 295.900
28 13.750 0.227 0.250 295.921 1538.910 296.437 295.888
29 14.250 0.231 0.285 295.923 1540.024 296.422 295.872
30 14.750 0.234 0.325 295.927 1540.859 296.410 295.861
31 15.250 0.234 0.371 295.933 1541.404 296.399 295.837
32 15.750 0.231 0.422 295.941 1541.622 296.389 295.814
33 16.250 0.226 0.482 295.951 1541.498 296.378 295.784
34 16.750 0.218 0.549 295.964 1541.021 296.362 295.752
35 17.250 0.207 0.626 295.978 1540.197 296.349 295.712
36 17.750 0.193 0.714 295.994 1539.045 296.335 295.662
37 18.250 0.175 0.814 296.011 1537.598 296.317 295.614
38 18.750 0.153 0.928 296.027 1535.918 296.301 295.558
39 19.250 0.127 1.058 296.043 1534.080 296.280 295.507
40 19.750 0.097 1.207 296.057 1532.174 296.264 295.470
41 20.250 0.062 1.376 296.069 1530.293 296.265 295.457
42 20.750 0.022 1.569 296.079 1528.527 296.364 295.550
43 21.250 0.000 1.780 296.088 1526.948 0.000 0.000
44 21.750 0.000 1.964 296.096 1525.528 0.000 0.000
45 22.250 0.000 2.124 296.104 1524.219 0.000 0.000
46 22.750 0.000 2.268 296.111 1522.996 0.000 0.000
47 23.250 0.000 2.398 296.119 1521.844 0.000 0.000
48 23.750 0.000 2.518 296.126 1520.752 0.000 0.000
49 24.250 0.000 2.629 296.132 1519.712 0.000 0.000
50 24.750 0.000 2.734 296.139 1518.717 0.000 0.000
51 25.250 0.000 2.833 296.145 1517.764 0.000 0.000
52 25.750 0.000 2.927 296.152 1516.848 0.000 0.000
53 26.250 0.000 3.017 296.158 1515.966 0.000 0.000
54 26.750 0.000 3.103 296.164 1515.116 0.000 0.000
55 27.250 0.000 3.185 296.170 1514.295 0.000 0.000
56 27.750 0.000 3.264 296.177 1513.501 0.000 0.000
57 28.250 0.000 3.341 296.183 1512.732 0.000 0.000
58 28.750 0.000 3.414 296.188 1511.986 0.000 0.000
59 29.250 0.000 3.486 296.194 1511.263 0.000 0.000
60 29.750 0.000 3.555 296.200 1510.561 0.000 0.000
61 30.250 0.000 3.623 296.206 1509.878 0.000 0.000
62 30.750 0.000 3.688 296.212 1509.214 0.000 0.000
63 31.250 0.000 3.752 296.218 1508.568 0.000 0.000
64 31.750 0.000 3.814 296.223 1507.938 0.000 0.000
65 32.250 0.000 3.875 296.229 1507.323 0.000 0.000
66 32.750 0.000 3.934 296.235 1506.724 0.000 0.000
67 33.250 0.000 3.992 296.241 1506.139 0.000 0.000
68 33.750 0.000 4.049 296.246 1505.567 0.000 0.000
69 34.250 0.000 4.104 296.252 1505.009 0.000 0.000
70 34.750 0.000 4.159 296.257 1504.462 0.000 0.000
71 35.250 0.000 4.212 296.263 1503.927 0.000 0.000
72 35.750 0.000 4.264 296.269 1503.403 0.000 0.000
73 36.250 0.000 4.315 296.274 1502.889 0.000 0.000
74 36.750 0.000 4.366 296.280 1502.386 0.000 0.000
75 37.250 0.000 4.415 296.286 1501.892 0.000 0.000
76 37.750 0.000 4.464 296.291 1501.407 0.000 0.000
77 38.250 0.000 4.512 296.297 1500.931 0.000 0.000
78 38.750 0.000 4.559 296.303 1500.464 0.000 0.000
79 39.250 0.000 4.605 296.308 1500.004 0.000 0.000
80 39.750 0.000 4.650 296.314 1499.552 0.000 0.000
81 40.250 0.000 4.695 296.320 1499.107 0.000 0.000
82 40.750 0.000 4.739 296.325 1498.669 0.000 0.000
83 41.250 0.000 4.783 296.331 1498.238 0.000 0.000
84 41.750 0.000 4.826 296.337 1497.813 0.000 0.000
85 42.250 0.000 4.868 296.342 1497.394 0.000 0.000
86 42.750 0.000 4.910 296.348 1496.981 0.000 0.000
87 43.250 0.000 4.951 296.354 1496.574 0.000 0.000
88 43.750 0.000 4.992 296.360 1496.171 0.000 0.000
89 44.250 0.000 5.032 296.365 1495.774 0.000 0.000
90 44.750 0.000 5.072 296.371 1495.382 0.000 0.000
91 45.250 0.000 5.111 296.377 1494.994 0.000 0.000
92 45.750 0.000 5.150 296.383 1494.611 0.000 0.000