Surface Fluxes’ Diurnal Cycle
Table of contents
Code
Main program
sp_07_01.m | View on GitHub
% Supplemental program 7.1
% --- Physical constants
physcon.vkc = 0.4; % von Karman constant
physcon.grav = 9.80665; % Gravitational acceleration (m/s2)
physcon.tfrz = 273.15; % Freezing point of water (K)
physcon.sigma = 5.67e-08; % Stefan-Boltzmann constant (W/m2/K4)
physcon.mmdry = 28.97 / 1000; % Molecular mass of dry air (kg/mol)
physcon.mmh2o = 18.02 / 1000; % Molecular mass of water (kg/mol)
physcon.cpd = 1005.0; % Specific heat of dry air at constant pressure (J/kg/K)
physcon.cpw = 1846.0; % Specific heat of water vapor at constant pressure (J/kg/K)
physcon.rgas = 8.31446; % Universal gas constant (J/K/mol)
physcon.cwat = 4188.0; % Specific heat of water (J/kg/K)
physcon.cice = 2117.27; % Specific heat ice (J/kg/K)
physcon.rhowat = 1000.0; % Density of water (kg/m3)
physcon.rhoice = 917.0; % Density of ice (kg/m3)
physcon.cvwat = physcon.cwat * physcon.rhowat; % Heat capacity of water (J/m3/K)
physcon.cvice = physcon.cice * physcon.rhoice; % Heat capacity of ice (J/m3/K)
physcon.tkwat = 0.57; % Thermal conductivity of water (W/m/K)
physcon.tkice = 2.29; % Thermal conductivity of ice (W/m/K)
physcon.hfus = 0.3337e6; % Heat of fusion for water at 0 C (J/kg)
physcon.hvap = 2.501e6; % Latent heat of evaporation (J/kg)
physcon.hsub = physcon.hfus + physcon.hvap; % Latent heat of sublimation (J/kg)
% --- Initialize soil texture variables
% Soil texture classes (Cosby et al. 1984. Water Resources Research 20:682-690)
% 1: sand
% 2: loamy sand
% 3: sandy loam
% 4: silty loam
% 5: loam
% 6: sandy clay loam
% 7 silty clay loam
% 8: clay loam
% 9: sandy clay
% 10: silty clay
% 11: clay
soilvar.silt = [ 5.0, 12.0, 32.0, 70.0, 39.0, 15.0, 56.0, 34.0, 6.0, 47.0, 20.0]; % Percent silt
soilvar.sand = [92.0, 82.0, 58.0, 17.0, 43.0, 58.0, 10.0, 32.0, 52.0, 6.0, 22.0]; % Percent sand
soilvar.clay = [ 3.0, 6.0, 10.0, 13.0, 18.0, 27.0, 34.0, 34.0, 42.0, 47.0, 58.0]; % Percent clay
% Volumetric soil water content at saturation (porosity)
% (Clapp and Hornberger. 1978. Water Resources Research 14:601-604)
soilvar.watsat = [0.395, 0.410, 0.435, 0.485, 0.451, 0.420, 0.477, 0.476, 0.426, 0.492, 0.482];
% --- Model run control parameters
dt = 1800; % Time step (seconds)
nday = 30; % Number of days to simulate, repeating the same diurnal cycle
soilvar.method = 'excess-heat'; % Phase change: use 'excess-heat' or 'apparent-heat-capacity'
fluxvar.profiles = 'MOST'; % Use Monin-Obukhov similarity theory
% fluxvar.profiles = 'RSL'; % Use canopy coupling with roughness sublayer theory
fluxvar.bucket = 'no_bucket'; % Soil wetness factor = 1
% fluxvar.bucket = 'use_bucket'; % Use bucket model hydrology for soil wetness factor
% --- Atmospheric forcing at a reference height
forcvar.zref = 30.0; % Reference height (m)
tmean = 25.0; % Mean daily air temperature (C)
trange = 10.0; % Temperature range for diurnal cycle (C)
relhum = 70.0; % Relative humidity (%)
forcvar.uref = 3.0; % Wind speed at reference height (m/s)
forcvar.pref = 101325; % Atmospheric pressure (Pa)
forcvar.rain = 0.0; % Rainfall (kg H2O/m2/s)
forcvar.snow = 0.0; % Snowfall (kg H2O/m2/s)
doy = 182.0; % Day of year (1 to 365) for solar radiation
lat = 40.0 * pi/180; % Latitude (degrees -> radians) for solar radiation
solcon = 1364.0; % Solar constant (W/m2)
% --- Site characteristics
vis = 1; nir = 2; % Waveband indices for visible and near-infrared
alb_surf(vis) = 0.10; % Snow-free surface albedo for visible waveband (-)
alb_surf(nir) = 0.20; % Snow-free surface albedo for near-infrared waveband (-)
alb_snow(vis) = 0.95; % Snow albedo for visible waveband (-)
alb_snow(nir) = 0.70; % Snow albedo for near-infrared waveband (-)
surfvar.emiss = 0.98; % Surface emissivity (dimensionless)
snow_mask = 100.0; % Snow albedo masking depth (kg H2O/m2)
soilvar.soil_texture = 5; % Soil texture class
bucket.soil_water_max = 150.0; % Maximum soil water (kg H2O/m2)
bucket.soil_beta_max = 0.75; % Soil water at which soil_beta = 1 (fraction of soil_water_max)
surfvar.hc = 20.0; % Canopy height (m)
%surfvar.hc = 0.5;
%forcvar.zref = 10.5;
surfvar.LAI = 5.0; % Leaf area index (m2/m2)
% For Harman and Finnigan (2007, 2008) roughness sublayer (RSL)
lad = surfvar.LAI / surfvar.hc; % Leaf area density (m2/m3)
cd = 0.20; % Leaf drag coefficient (dimensionless)
surfvar.Lc = 1 / (cd * lad); % Canopy density length scale (m)
surfvar.rc = 0.2; % Leaf Nusselt number (heat) or Stanton number (scalar)
% For Monin-Obukhov parameterization (MOST)
fluxvar.disp = 0.67 * surfvar.hc; % Displacement height (m)
fluxvar.z0m = 0.13 * surfvar.hc; % Roughness length for momentum (m)
fluxvar.z0c = 0.10 * fluxvar.z0m; % Roughness length for scalars (m)
% --- Soil variables
% Number of layers in soil profile
soilvar.nsoi = 10;
% Soil layer thickness (m)
soilvar.dz = [0.0175, 0.0276, 0.0455, 0.0750, 0.1236, 0.2038, 0.3360, 0.5539, 0.9133, 1.5058];
% Soil depth (m) at i+1/2 interface between layers i and i+1 (negative distance from surface)
soilvar.z_plus_onehalf(1) = -soilvar.dz(1);
for i = 2:soilvar.nsoi
soilvar.z_plus_onehalf(i) = soilvar.z_plus_onehalf(i-1) - soilvar.dz(i);
end
% Soil depth (m) at center of layer i (negative distance from surface)
soilvar.z(1) = 0.5 * soilvar.z_plus_onehalf(1);
for i = 2:soilvar.nsoi
soilvar.z(i) = 0.5 * (soilvar.z_plus_onehalf(i-1) + soilvar.z_plus_onehalf(i));
end
% Thickness between between z(i) and z(i+1)
for i = 1:soilvar.nsoi-1
soilvar.dz_plus_onehalf(i) = soilvar.z(i) - soilvar.z(i+1);
end
soilvar.dz_plus_onehalf(soilvar.nsoi) = 0.5 * soilvar.dz(soilvar.nsoi);
% --- Initial conditions
% Initial soil temperature (K) and unfrozen and frozen water (kg H2O/m2)
for i = 1:soilvar.nsoi
% Temperature
soilvar.tsoi(i) = tmean + physcon.tfrz;
% Soil water at saturation (kg H2O/m2)
h2osoi_sat = soilvar.watsat(soilvar.soil_texture) * physcon.rhowat * soilvar.dz(i);
% Actual water content is some fraction of saturation. These are only used for soil
% thermal properties and phase change. Note the inconsistency with the use of soil
% water in the bucket model to calculate the soil wetness factor.
satfrac = 0.85;
if (soilvar.tsoi(i) > physcon.tfrz)
soilvar.h2osoi_ice(i) = 0;
soilvar.h2osoi_liq(i) = satfrac * h2osoi_sat;
else
soilvar.h2osoi_liq(i) = 0;
soilvar.h2osoi_ice(i) = satfrac * h2osoi_sat;
end
end
% Initial surface temperature (K) and vapor pressure (Pa)
fluxvar.tsrf = soilvar.tsoi(1);
[esat, desat] = satvap (fluxvar.tsrf-physcon.tfrz);
fluxvar.esrf = esat;
% Bucket model snow and soil water (kg H2O/m2)
bucket.snow_water = 0;
bucket.soil_water = bucket.soil_water_max;
% --- Time stepping loop
% Main loop is NTIM iterations per day with a time step of DT seconds.
% This is repeated NDAY times to spinup the model from arbitrary initial
% soil temperatures.
ntim = round(86400/dt);
for j = 1:nday
fprintf('day = %6.0f\n',j)
for i = 1:ntim
% Hour of day (0 to 24)
hour = i * (dt/86400 * 24);
% Air temperature (K): use a sine wave with max (tmean + 1/2 trange) at 1400
% and min (tmean - 1/2 trange) at 0200
forcvar.tref = tmean + 0.5 * trange * sin(2*pi/24 * (hour-8)) + physcon.tfrz;
% Vapor pressure (Pa) using constant relative humidity
[esat, desat] = satvap (forcvar.tref-physcon.tfrz);
forcvar.eref = (relhum / 100) * esat;
% Derived quantities
% forcvar.thref ! Potential temperature at reference height (K)
% forcvar.qref ! Specific humidity at reference height (kg/kg)
% forcvar.thvref ! Virtual potential temperature at reference height (K)
% forcvar.rhomol ! Molar density at reference height (mol/m3)
% forcvar.rhoair ! Air density at reference height (kg/m3)
% forcvar.mmair ! Molecular mass of air at reference height (kg/mol)
% forcvar.cpair ! Specific heat of air at constant pressure, at reference height (J/mol/K)
forcvar.thref = forcvar.tref + 0.0098 * forcvar.zref;
forcvar.qref = physcon.mmh2o / physcon.mmdry * forcvar.eref / ...
(forcvar.pref - (1 - physcon.mmh2o/physcon.mmdry) * forcvar.eref);
forcvar.thvref = forcvar.thref * (1 + 0.61 * forcvar.qref);
forcvar.rhomol = forcvar.pref / (physcon.rgas * forcvar.tref);
forcvar.rhoair = forcvar.rhomol * physcon.mmdry * ...
(1 - (1 - physcon.mmh2o/physcon.mmdry) * forcvar.eref / forcvar.pref);
forcvar.mmair = forcvar.rhoair / forcvar.rhomol;
forcvar.cpair = physcon.cpd * (1 + (physcon.cpw/physcon.cpd - 1) * forcvar.qref); % J/kg/K
forcvar.cpair = forcvar.cpair * forcvar.mmair; % J/mol/K
% Solar radiation (W/m2)
% doy ! Day of year (1 to 365)
% lat ! Latitude (radians)
% decl ! Declination (radians): Brock, T.D. (1981) Calculating solar radiation
% ! for ecological studies. Ecological Modelling 14:1-19
% hour_angle ! Solar hour angle (radians)
% coszen ! Cosine of solar zenith angle
% rv ! Radius vector: Brock, T.D. 1981. Calculating solar radiation
% ! for ecological studies. Ecological Modelling 14:1-19
% soltoa ! Solar radiation on horizontal surface at top of atmosphere (W/m2)
% tau_atm ! Atmospheric transmission coefficient
% oam ! Optical air mass
% soldir ! Direct beam solar radiation on horizontal surface (W/m2)
% soldif ! Diffuse solar radiation on horizontal surface (W/m2)
% solrad ! Total solar radiation on horizontal surface (W/m2)
% Solar radiation at top of the atmosphere
decl = 23.45 * sin((284+doy)/365*2*pi) * pi/180;
hour_angle = 15 * (hour-12) * pi/180;
coszen = max(cos(lat)*cos(decl)*cos(hour_angle) + sin(lat)*sin(decl), 0);
rv = 1 / sqrt(1 + 0.033*cos(doy/365*2*pi));
soltoa = solcon / rv^2 * coszen;
% Clear sky atmospheric attenuation: Gates, D.M. (1980) Biophysical Ecology, page 110, 115
tau_atm = 0.5;
oam = 1 / max(coszen, 0.04);
soldir = soltoa * tau_atm^oam; % Clear sky direct beam
soldif = soltoa * (0.271 - 0.294 * tau_atm^oam); % Clear sky diffuse
forcvar.solrad = soldir + soldif; % Total at surface
% Longwave radiation (W/m2)
forcvar.lwdown = (0.398e-05 * forcvar.tref^2.148) * physcon.sigma * forcvar.tref^4;
% Effective surface albedo is weighted combination of snow-free and
% snow albedos
fsno = bucket.snow_water / (bucket.snow_water + snow_mask);
alb_eff(vis) = alb_surf(vis) * (1 - fsno) + alb_snow(vis) * fsno;
alb_eff(nir) = alb_surf(nir) * (1 - fsno) + alb_snow(nir) * fsno;
% Radiative forcing: absorbed solar + incident longwave. This partitions
% solar radiation into 50% visible and 50% near-infrared wavebands.
fluxvar.qa = (1-alb_eff(vis)) * 0.5*forcvar.solrad ...
+ (1-alb_eff(nir)) * 0.5*forcvar.solrad + surfvar.emiss * forcvar.lwdown;
% Canopy conductance (mol/m2/s) - use a weighted average of sunlit and shaded leaves
gcan_min = 0.05; % Minimum conductance (mol/m2/s)
gcan_max = 0.2; % Maximum conductance (mol/m2/s)
ext = 0.5 / max(coszen, 0.0001); % Light extinction coefficient
fsun = (1 - exp(-ext*surfvar.LAI)) / (ext*surfvar.LAI); % Sunlit fraction of canopy
if (soldir+soldif > 0)
surfvar.gcan = (fsun * gcan_max + (1 - fsun) * gcan_min) * surfvar.LAI;
else
surfvar.gcan = gcan_min * surfvar.LAI;
end
% Thermal conductivity and heat capacity
[soilvar] = soil_thermal_properties (physcon, soilvar);
% Calculate the soil temperatures and surface fluxes
[fluxvar, soilvar, bucket] = surface_fluxes (physcon, forcvar, surfvar, soilvar, fluxvar, bucket, dt);
% Rainfall to equal evaporative loss (kg H2O/m2/s)
% forcvar.rain = fluxvar.etflx * physcon.mmh2o;
forcvar.rain = 0;
% Bucket model hydrology
[bucket] = bucket_hydrology (physcon, forcvar, fluxvar, bucket, dt);
% Save data for graphics
xhour(i) = hour;
ytsrf(i) = fluxvar.tsrf - physcon.tfrz;
ytref(i) = forcvar.tref - physcon.tfrz;
yrnet(i) = fluxvar.rnet;
yshflx(i) = fluxvar.shflx;
ylhflx(i) = fluxvar.lhflx;
ygsoi(i) = fluxvar.gsoi;
yustar(i) = fluxvar.ustar;
ygac(i) = fluxvar.gac * 100;
ygcan(i) = surfvar.gcan * 100;
end
end
% --- Write output files
A = [xhour; ytref; ytsrf; yrnet; yshflx; ylhflx; ygsoi; yustar; ygac; ygcan];
fileID = fopen('flux.txt','w');
fprintf(fileID,'%12s %12s %12s %12s %12s %12s %12s %12s %12s %12s\n','hour','Ta','Ts','Rn','H','LE','G','ustar','gac','gcan');
fprintf(fileID,'%12.3f %12.3f %12.3f %12.3f %12.3f %12.3f %12.3f %12.3f %12.3f %12.3f\n', A);
fclose(fileID);
B = [soilvar.z; soilvar.tsoi];
fileID = fopen('tsoi.txt','w');
fprintf(fileID,'%12s %12s\n','depth','tsoi');
fprintf(fileID,'%12.3f %12.3f\n', B);
fclose(fileID);
% --- Make graph
plot(xhour,yrnet,'g-',xhour,yshflx,'r-',xhour,ylhflx,'b-',xhour,ygsoi,'r--',xhour,ygac,'m-')
axis([0 24 -100 600])
set(gca,'xTick',0:3:24)
set(gca,'yTick',-100:100:800)
title('Diurnal cycle')
xlabel('Time of day (hours)')
ylabel('Flux (W m^{-2})')
legend('R_n','H','\lambdaE','G','g_{ac}*100','Location','northwest')
Aux. programs
brent_root.m | View on GitHub
function [fluxvar, root] = brent_root (func, physcon, forcvar, surfvar, fluxvar, xa, xb, tol)
% Use Brent's method to find the root of a function, which is known to exist between
% xa and xb. The root is updated until its accuracy is tol. func is the name of the
% function to solve. The variable root is returned as the root of the function. The
% function being evaluated has the definition statement:
%
% function [fluxvar, fx] = func (physcon, forcvar, surfvar, fluxvar, x)
%
% The function func is exaluated at x and the returned value is fx. It uses variables
% in the physcon, forcvar, surfvar, and fluxvar structures. These are passed in as
% input arguments. It also calculates values for variables in the fluxvar structure
% so this must be returned in the function call as an output argument. The matlab
% function feval evaluates func.
% --- Evaluate func at xa and xb and make sure the root is bracketed
a = xa;
b = xb;
[fluxvar, fa] = feval(func, physcon, forcvar, surfvar, fluxvar, a);
[fluxvar, fb] = feval(func, physcon, forcvar, surfvar, fluxvar, b);
if ((fa > 0 & fb > 0) | (fa < 0 & fb < 0))
error('brent_root error: root must be bracketed')
end
% --- Initialize iteration
itmax = 50; % Maximum number of iterations
eps1 = 1e-08; % Relative error tolerance
c = b;
fc = fb;
% --- Iterative root calculation
for iter = 1:itmax
if ((fb > 0 & fc > 0) | (fb < 0 & fc < 0))
c = a;
fc = fa;
d = b - a;
e = d;
end
if (abs(fc) < abs(fb))
a = b;
b = c;
c = a;
fa = fb;
fb = fc;
fc = fa;
end
tol1 = 2 * eps1 * abs(b) + 0.5 * tol;
xm = 0.5 * (c - b);
% Check to end iteration
if (abs(xm) <= tol1 | fb == 0)
break
end
if (abs(e) >= tol1 & abs(fa) > abs(fb))
s = fb / fa;
if (a == c)
p = 2 * xm * s;
q = 1 - s;
else
q = fa / fc;
r = fb / fc;
p = s * (2 * xm * q * (q - r) - (b - a) * (r - 1));
q = (q - 1) * (r - 1) * (s - 1);
end
if (p > 0)
q = -q;
end
p = abs(p);
if (2*p < min(3*xm*q-abs(tol1*q), abs(e*q)))
e = d;
d = p / q;
else
d = xm;
e = d;
end
else
d = xm;
e = d;
end
a = b;
fa = fb;
if (abs(d) > tol1)
b = b + d;
else
if (xm >= 0)
b = b + abs(tol1);
else
b = b - abs(tol1);
end
end
[fluxvar, fb] = feval(func, physcon, forcvar, surfvar, fluxvar, b);
% Check to end iteration
if (fb == 0)
break
end
% Check to see if failed to converge
if (iter == itmax)
error('brent_root error: Maximum number of interations exceeded')
end
end
root = b;
bucket_hydrology.m | View on GitHub
function [bucket] = bucket_hydrology (physcon, forcvar, fluxvar, bucket, dt)
% Bucket model hydrology
% ------------------------------------------------------
% Input
% dt ! Time step (s)
% physcon.mmh2o ! Molecular mass of water (kg/mol)
% forcvar.rain ! Rainfall (kg H2O/m2/s)
% forcvar.snow ! Snowfall (kg H2O/m2/s)
% fluxvar.etflx ! Evapotranspiration (mol H2O/m2/s)
% bucket.snow_melt ! Snow melt (kg H2O/m2/s)
% bucket.soil_water_max ! Maximum soil water (kg H2O/m2)
%
% Input/output
% bucket.snow_water ! Snow water (kg H2O/m2)
% bucket.soil_water ! Soil water (kg H2O/m2)
%
% Output
% bucket.runoff ! Runoff (kg H2O/m2/s)
% ------------------------------------------------------
% --- Save current water for conservation check
snow0 = bucket.snow_water;
soil0 = bucket.soil_water;
tot0 = snow0 + soil0;
% --- Update snow and soil water for snow melt
bucket.snow_water = bucket.snow_water - bucket.snow_melt * dt;
bucket.soil_water = bucket.soil_water + bucket.snow_melt * dt;
% --- Update snow and soil water for precipitation
bucket.soil_water = bucket.soil_water + forcvar.rain * dt;
bucket.snow_water = bucket.snow_water + forcvar.snow * dt;
% --- Update snow and soil water for evaporative flux
% Evaporative loss (kg H2O/m2/s)
evap = fluxvar.etflx * physcon.mmh2o;
% Apply evaporative flux to snow, but if more snow sublimates than
% is present take the extra water from the soil as evaporation
subl = min (evap, bucket.snow_water/dt);
evap = evap - subl;
% Update snow and soil
bucket.snow_water = bucket.snow_water - subl * dt;
bucket.soil_water = bucket.soil_water - evap * dt;
% --- Runoff is soil water in excess of a maximum capacity
bucket.runoff = max ((bucket.soil_water - bucket.soil_water_max)/dt, 0);
bucket.soil_water = bucket.soil_water - bucket.runoff * dt;
% --- Conservation check
% Snow water
delta = bucket.snow_water - snow0;
err = (forcvar.snow - bucket.snow_melt - subl) * dt - delta;
if (abs(err) > 1e-03)
error ('Bucket model snow conservation error')
end
% Soil water
delta = bucket.soil_water - soil0;
err = (forcvar.rain + bucket.snow_melt - evap - bucket.runoff) * dt - delta;
if (abs(err) > 1e-03)
error ('Bucket model soil conservation error')
end
% Total water
delta = (bucket.snow_water + bucket.soil_water) - tot0;
err = (forcvar.rain + forcvar.snow - fluxvar.etflx * physcon.mmh2o - bucket.runoff) * dt - delta;
if (abs(err) > 1e-03)
error ('Bucket model total conservation error')
end
hybrid_root.m | View on GitHub
function [fluxvar, root] = hybrid_root (func, physcon, forcvar, surfvar, fluxvar, xa, xb, tol)
% Solve for the root of a function using the secant and Brent's methods given
% initial estimates xa and xb. The root is updated until its accuracy is tol.
% func is the name of the function to solve. The variable root is returned as
% the root of the function. The function being evaluated has the definition statement:
%
% function [fluxvar, fx] = func (physcon, forcvar, surfvar, fluxvar, x)
%
% The function func is exaluated at x and the returned value is fx. It uses variables
% in the physcon, forcvar, surfvar, and fluxvar structures. These are passed in as
% input arguments. It also calculates values for variables in the fluxvar structure
% so this must be returned in the function call as an output argument. The matlab
% function feval evaluates func.
% --- Evaluate func at xa and see if this is the root
x0 = xa;
[fluxvar, f0] = feval(func, physcon, forcvar, surfvar, fluxvar, x0);
if (f0 == 0)
root = x0;
return
end
% --- Evaluate func at xb and see if this is the root
x1 = xb;
[fluxvar, f1] = feval(func, physcon, forcvar, surfvar, fluxvar, x1);
if (f1 == 0)
root = x1;
return
end
% --- Order initial root estimates correctly
if (f1 < f0)
minx = x1;
minf = f1;
else
minx = x0;
minf = f0;
end
% --- Iterative root calculation. Use the secant method, with Brent's method as a backup
itmax = 40;
for iter = 1:itmax
dx = -f1 * (x1 - x0) / (f1 - f0);
x = x1 + dx;
% Check if x is the root. If so, exit the iteration
if (abs(dx) < tol)
x0 = x;
break
end
% Evaluate the function at x
x0 = x1;
f0 = f1;
x1 = x;
[fluxvar, f1] = feval(func, physcon, forcvar, surfvar, fluxvar, x1);
if (f1 < minf)
minx = x1;
minf = f1;
end
% If a root zone is found, use Brent's method for a robust backup strategy
% and exit the iteration
if (f1 * f0 < 0)
[fluxvar, x] = brent_root (func, physcon, forcvar, surfvar, fluxvar, x0, x1, tol);
x0 = x;
break
end
% In case of failing to converge within itmax iterations stop at the minimum function
if (iter == itmax)
[fluxvar, f1] = feval(func, physcon, forcvar, surfvar, fluxvar, minx);
x0 = minx;
end
end
root = x0;
most.m | View on GitHub
function [fluxvar, fx] = most (physcon, forcvar, surfvar, fluxvar, x)
% Use Monin-Obukhov similarity theory to obtain the Obukhov length (obu).
% This is the function to solve for the Obukhov length. For the current
% estimate of the Obukhov length (x), calculate u*, T*, and q* and then
% the new length (obu). The function value is the change in Obukhov length:
% fx = x - obu.
% -------------------------------------------------------------------------
% Input
% x ! Current estimate for Obukhov length (m)
% physcon.vkc ! von Karman constant
% physcon.grav ! Gravitational acceleration (m/s2)
% physcon.mmh2o ! Molecular mass of water (kg/mol)
% forcvar.zref ! Reference height (m)
% forcvar.uref ! Wind speed at reference height (m/s)
% forcvar.thref ! Potential temperature at reference height (K)
% forcvar.thvref ! Virtual potential temperature at reference height (K)
% forcvar.eref ! Vapor pressure at reference height (Pa)
% forcvar.pref ! Atmospheric pressure (Pa)
% forcvar.mmair ! Molecular mass of air at reference height (kg/mol)
% fluxvar.tsrf ! Surface temperature (K)
% fluxvar.esrf ! Surface vapor pressure (Pa)
% fluxvar.z0m ! Roughness length for momentum (m)
% fluxvar.z0c ! Roughness length for scalars (m)
% fluxvar.disp ! Displacement height (m)
% Output
% fluxvar.ustar ! Friction velocity (m/s)
% fluxvar.tstar ! Temperature scale (K)
% fluxvar.qstar ! Water vapor scale (mol/mol)
% fluxvar.obu ! Obukhov length (m)
% fx ! Change in Obukhov length (x - obu)
% -------------------------------------------------------------------------
% --- Prevent near-zero values of the Obukhov length
if (abs(x) <= 0.1)
x = 0.1;
end
% --- Calculate z-d at the reference height, because this is used many times
z_minus_d = forcvar.zref - fluxvar.disp;
% --- Evaluate psi for momentum at the reference height (zref-disp) and surface (z0m)
[psi_m_zref] = psi_m_monin_obukhov (z_minus_d / x);
[psi_m_z0m] = psi_m_monin_obukhov (fluxvar.z0m / x);
psim = -psi_m_zref + psi_m_z0m;
% --- Evaluate psi for scalars at the reference height (zref-disp) and surface (z0c)
[psi_c_zref] = psi_c_monin_obukhov (z_minus_d / x);
[psi_c_z0c] = psi_c_monin_obukhov (fluxvar.z0c / x);
psic = -psi_c_zref + psi_c_z0c;
% --- Calculate u* (m/s), T* (K), q* (mol/mol), and Tv* (K)
zlog_m = log(z_minus_d / fluxvar.z0m);
zlog_c = log(z_minus_d / fluxvar.z0c);
fluxvar.ustar = forcvar.uref * physcon.vkc / (zlog_m + psim);
fluxvar.tstar = (forcvar.thref - fluxvar.tsrf) * physcon.vkc / (zlog_c + psic);
fluxvar.qstar = (forcvar.eref - fluxvar.esrf) / forcvar.pref * physcon.vkc / (zlog_c + psic);
tvstar = fluxvar.tstar + 0.61 * forcvar.thref * fluxvar.qstar * (physcon.mmh2o / forcvar.mmair);
% --- Calculate Obukhov length (m)
fluxvar.obu = fluxvar.ustar^2 * forcvar.thvref / (physcon.vkc * physcon.grav * tvstar);
% --- Calculate change in obu
fx = x - fluxvar.obu;
phase_change.m | View on GitHub
function [soilvar] = phase_change (physcon, soilvar, dt)
% Adjust temperatures for phase change. Freeze or melt ice using
% energy excess or deficit needed to change temperature to the
% freezing point.
% ------------------------------------------------------
% Input
% dt ! Time step (s)
% physcon.hfus ! Heat of fusion for water at 0 C (J/kg)
% physcon.tfrz ! Freezing point of water (K)
% soilvar.nsoi ! Number of soil layers
% soilvar.dz ! Soil layer thickness (m)
% soilvar.cv ! Volumetric heat capacity (J/m3/K)
%
% Input/output
% soilvar.tsoi ! Soil temperature (K)
% soilvar.h2osoi_liq ! Unfrozen water, liquid (kg H2O/m2)
% soilvar.h2osoi_ice ! Frozen water, ice (kg H2O/m2)
%
% Output
% soilvar.hfsoi ! Soil phase change energy flux (W/m2)
% ------------------------------------------------------
% --- Initialize total soil heat of fusion to zero
soilvar.hfsoi = 0;
% --- Now loop over all soil layers to calculate phase change
for i = 1:soilvar.nsoi
% --- Save variables prior to phase change
wliq0 = soilvar.h2osoi_liq(i); % Amount of liquid water before phase change
wice0 = soilvar.h2osoi_ice(i); % Amount of ice before phase change
wmass0 = wliq0 + wice0; % Amount of total water before phase change
tsoi0 = soilvar.tsoi(i); % Soil temperature before phase change
% --- Identify melting or freezing layers and set temperature to freezing
% Default condition is no phase change (imelt = 0)
imelt = 0;
% Melting: if ice exists above melt point, melt some to liquid.
% Identify melting by imelt = 1
if (soilvar.h2osoi_ice(i) > 0 & soilvar.tsoi(i) > physcon.tfrz)
imelt = 1;
soilvar.tsoi(i) = physcon.tfrz;
end
% Freezing: if liquid exists below melt point, freeze some to ice.
% Identify freezing by imelt = 2
if (soilvar.h2osoi_liq(i) > 0 & soilvar.tsoi(i) < physcon.tfrz)
imelt = 2;
soilvar.tsoi(i) = physcon.tfrz;
end
% --- Calculate energy for freezing or melting
% The energy for freezing or melting (W/m2) is assessed from the energy
% excess or deficit needed to change temperature to the freezing point.
% This is a potential energy flux, because cannot melt more ice than is
% present or freeze more liquid water than is present.
%
% heat_flux_pot > 0: freezing; heat_flux_pot < 0: melting
if (imelt > 0)
heat_flux_pot = (soilvar.tsoi(i) - tsoi0) * soilvar.cv(i) * soilvar.dz(i) / dt;
else
heat_flux_pot = 0;
end
% Maximum energy for melting or freezing (W/m2)
if (imelt == 1)
heat_flux_max = -soilvar.h2osoi_ice(i) * physcon.hfus / dt;
end
if (imelt == 2)
heat_flux_max = soilvar.h2osoi_liq(i) * physcon.hfus / dt;
end
% --- Now freeze or melt ice
if (imelt > 0)
% Change in ice (kg H2O/m2/s): freeze (+) or melt (-)
ice_flux = heat_flux_pot / physcon.hfus;
% Update ice (kg H2O/m2)
soilvar.h2osoi_ice(i) = wice0 + ice_flux * dt;
% Cannot melt more ice than is present
soilvar.h2osoi_ice(i) = max(0, soilvar.h2osoi_ice(i));
% Ice cannot exceed total water that is present
soilvar.h2osoi_ice(i) = min(wmass0, soilvar.h2osoi_ice(i));
% Update liquid water (kg H2O/m2) for change in ice
soilvar.h2osoi_liq(i) = max(0, (wmass0-soilvar.h2osoi_ice(i)));
% Actual energy flux from phase change (W/m2). This is equal to
% heat_flux_pot except if tried to melt too much ice.
heat_flux = physcon.hfus * (soilvar.h2osoi_ice(i) - wice0) / dt;
% Sum energy flux from phase change (W/m2)
soilvar.hfsoi = soilvar.hfsoi + heat_flux;
% Residual energy not used in phase change is added to soil temperature
residual = heat_flux_pot - heat_flux;
soilvar.tsoi(i) = soilvar.tsoi(i) - residual * dt / (soilvar.cv(i) * soilvar.dz(i));
% Error check: make sure actual phase change does not exceed permissible phase change
if (abs(heat_flux) > abs(heat_flux_max))
error ('Soil temperature energy conservation error: phase change')
end
% Freezing: make sure actual phase change does not exceed permissible phase change
% and that the change in ice does not exceed permissible change
if (imelt == 2)
% Energy flux (W/m2)
constraint = min(heat_flux_pot, heat_flux_max);
err = heat_flux - constraint;
if (abs(err) > 1e-03)
error ('Soil temperature energy conservation error: freezing energy flux')
end
% Change in ice (kg H2O/m2)
err = (soilvar.h2osoi_ice(i) - wice0) - constraint / physcon.hfus * dt;
if (abs(err) > 1e-03)
error ('Soil temperature energy conservation error: freezing ice flux')
end
end
% Thawing: make sure actual phase change does not exceed permissible phase change
% and that the change in ice does not exceed permissible change
if (imelt == 1)
% Energy flux (W/m2)
constraint = max(heat_flux_pot, heat_flux_max);
err = heat_flux - constraint;
if (abs(err) > 1e-03)
error ('Soil temperature energy conservation error: thawing energy flux')
end
% Change in ice (kg H2O/m2)
err = (soilvar.h2osoi_ice(i) - wice0) - constraint / physcon.hfus * dt;
if (abs(err) > 1e-03)
error ('Soil temperature energy conservation error: thawing ice flux')
end
end
end
end
phi_c_monin_obukhov.m | View on GitHub
function [phi_c] = phi_c_monin_obukhov (x)
% --- Evaluate the Monin-Obukhov phi function for scalars at x
if (x < 0)
phi_c = (1 - 16 * x)^(-0.5);
else
phi_c = 1 + 5 * x;
end
phi_m_monin_obukhov.m | View on GitHub
function [phi_m] = phi_m_monin_obukhov (x)
% --- Evaluate the Monin-Obukhov phi function for momentum at x
if (x < 0)
phi_m = (1 - 16 * x)^(-0.25);
else
phi_m = 1 + 5 * x;
end
psi_c_monin_obukhov.m | View on GitHub
function [psi_c] = psi_c_monin_obukhov (x)
% --- Evaluate the Monin-Obukhov psi function for scalars at x
if (x < 0)
y = (1 - 16 * x)^0.25;
psi_c = 2 * log((1 + y^2)/2);
else
psi_c = -5 * x;
end
psi_c_rsl.m | View on GitHub
function [psi_hat_c] = psi_c_rsl (z, h, L, c1, c2)
% --- Evaluate the roughness sublayer (RSL) function psi_hat for scalars
% at z. Note that z has already been adjusted for the displacement height
% (i.e., using z - d).
% ------------------------------------------------------
% Input
% z ! Vertical height - displacement height (m)
% h ! Canopy height - displacement height (m)
% L ! Obukhov length (m)
% c1 ! Parameter for RSL function phi_hat (dimensionless)
% c2 ! Parameter for RSL function phi_hat (dimensionless)
%
% Output
% psi_hat_c ! RSL psi_hat function for scalars (dimensionless)
% ------------------------------------------------------
% The function to integrate depends on unstable (f1) or stable (f2)
f1 = @(x) (1-16*x/L).^(-0.5) .* (1 - (1 - c1*exp(-c2*x/(2*h)))) ./ x;
f2 = @(x) (1+5*x/L) .* (1 - (1 - c1*exp(-c2*x/(2*h)))) ./ x;
% Numerically integrate the function from z to infinity
if (L < 0)
psi_hat_c = integral (f1, z, inf);
else
psi_hat_c = integral (f2, z, inf);
end
psi_m_monin_obukhov.m | View on GitHub
function [psi_m] = psi_m_monin_obukhov (x)
% --- Evaluate the Monin-Obukhov psi function for momentum at x
if (x < 0)
y = (1 - 16 * x)^0.25;
psi_m = 2 * log((1 + y)/2) + log((1 + y^2)/2) - 2 * atan(y) + pi / 2;
else
psi_m = -5 * x;
end
psi_m_rsl.m | View on GitHub
function [psi_hat_m] = psi_m_rsl (z, h, L, c1, c2)
% --- Evaluate the roughness sublayer (RSL) function psi_hat for momentum
% at z. Note that z has already been adjusted for the displacement height
% (i.e., using z - d).
% ------------------------------------------------------
% Input
% z ! Vertical height - displacement height (m)
% h ! Canopy height - displacement height (m)
% L ! Obukhov length (m)
% c1 ! Parameter for RSL function phi_hat (dimensionless)
% c2 ! Parameter for RSL function phi_hat (dimensionless)
%
% Output
% psi_hat_m ! RSL psi_hat function for momentum (dimensionless)
% ------------------------------------------------------
% The function to integrate depends on unstable (f1) or stable (f2)
f1 = @(x) (1-16*x/L).^(-0.25) .* (1 - (1 - c1*exp(-c2*x/(2*h)))) ./ x;
f2 = @(x) (1+5*x/L) .* (1 - (1 - c1*exp(-c2*x/(2*h)))) ./ x;
% Numerically integrate the function from z to infinity
if (L < 0)
psi_hat_m = integral (f1, z, inf);
else
psi_hat_m = integral (f2, z, inf);
end
rsl.m | View on GitHub
function [fluxvar, fx] = rsl (physcon, forcvar, surfvar, fluxvar, x)
% Use Harman & Finnigan (2007, 2008) roughness sublayer (RSL) theory to obtain
% the Obukhov length (obu). This is the function to solve for the Obukhov
% length. For the current estimate of the Obukhov length (x), calculate
% u*, T*, and q* and then the new length (obu). The function value is the
% change in Obukhov length: fx = x - obu.
% -------------------------------------------------------------------------
% Input
% x ! Current estimate for Obukhov length (m)
% physcon.vkc ! von Karman constant
% physcon.grav ! Gravitational acceleration (m/s2)
% physcon.mmh2o ! Molecular mass of water (kg/mol)
% forcvar.zref ! Reference height (m)
% forcvar.uref ! Wind speed at reference height (m/s)
% forcvar.thref ! Potential temperature at reference height (K)
% forcvar.thvref ! Virtual potential temperature at reference height (K)
% forcvar.eref ! Vapor pressure at reference height (Pa)
% forcvar.pref ! Atmospheric pressure (Pa)
% forcvar.mmair ! Molecular mass of air at reference height (kg/mol)
% fluxvar.tsrf ! Surface temperature (K)
% fluxvar.esrf ! Surface vapor pressure (Pa)
% surfvar.Lc ! Canopy density length scale (m)
% surfvar.hc ! Canopy height (m)
% surfvar.rc ! Leaf Nusselt number (heat) or Stanton number (scalar)
%
% Output
% fluxvar.z0m ! Roughness length for momentum (m)
% fluxvar.z0c ! Roughness length for scalars (m)
% fluxvar.disp ! Displacement height (m)
% fluxvar.ustar ! Friction velocity (m/s)
% fluxvar.tstar ! Temperature scale (K)
% fluxvar.qstar ! Water vapor scale (mol/mol)
% fluxvar.obu ! Obukhov length (m)
% fx ! Change in Obukhov length (x - obu)
% -------------------------------------------------------------------------
% --- Prevent near-zero values of Obukhov length
if (abs(x) <= 0.1)
x = 0.1;
end
% --- Determine beta_val = u* / u(h) for the current Obukhov length
% Neutral value for beta = u* / u(h)
beta_neutral = 0.35;
% Lc/obu
LcL = surfvar.Lc/x;
if (LcL <= 0)
% The unstable case is a quadratic equation for beta^2 at LcL
a = 1;
b = 16 * LcL * beta_neutral^4;
c = -beta_neutral^4;
beta_val = sqrt((-b + sqrt(b^2 - 4 * a * c)) / (2 * a));
% Error check
y = beta_val^2 * LcL;
fy = (1 - 16 * y)^(-0.25);
err = beta_val * fy - beta_neutral;
if (abs(err) > 1e-10)
error('unstable case: error in beta')
end
else
% The stable case is a cubic equation for beta at LcL
a = 5 * LcL;
b = 0;
c = 1;
d = -beta_neutral;
q = (2*b^3 - 9*a*b*c + 27*(a^2)*d)^2 - 4*(b^2 - 3*a*c)^3;
q = sqrt(q);
r = 0.5 * (q + 2*b^3 - 9*a*b*c + 27*(a^2)*d);
r = r^(1/3);
beta_val = -(b+r)/(3*a) - (b^2 - 3*a*c)/(3*a*r);
% Error check
y = beta_val^2 * LcL;
fy = 1 + 5 * y;
err = beta_val * fy - beta_neutral;
if (abs(err) > 1e-10)
error('stable case: error in beta')
end
end
% Place limits on beta
beta_val = min(0.5, max(beta_val,0.2));
% --- For current beta = u*/u(h) determine displacement height
dp = beta_val^2 * surfvar.Lc; % dp = hc - disp
fluxvar.disp = max(surfvar.hc - dp, 0); % Displacement height (m)
% Save reference height and canopy height (relative to displacement height),
% because these are used many times
z_minus_d = forcvar.zref - fluxvar.disp;
h_minus_d = surfvar.hc - fluxvar.disp;
% --- Turbulent Prandlt number (Pr) at canopy height
Prn = 0.5; % Neutral value for Pr
Prvr = 0.3; % Magnitude of variation of Pr with stability
Prsc = 2.0; % Scale of variation of Pr with stability
Pr = Prn + Prvr * tanh(Prsc*surfvar.Lc/x);
% --- The "f" parameter relates the length scale of the scalar (heat) to that of momentum
f = (sqrt(1 + 4 * surfvar.rc * Pr) - 1) / 2;
% --- Calculate the parameters c1 and c2 needed for the RSL function phi_hat
% Evaluate Monin-Obukhov phi functions at (hc-disp)/obu
[phi_m_hc] = phi_m_monin_obukhov (h_minus_d / x);
[phi_c_hc] = phi_c_monin_obukhov (h_minus_d / x);
% Roughness sublayer depth scale multiplier (dimensionless)
c2 = 0.5;
% c1 for momentum and scalars (dimensionless)
c1m = (1 - physcon.vkc / (2 * beta_val * phi_m_hc)) * exp(c2/2);
c1c = (1 - Pr*physcon.vkc / (2 * beta_val * phi_c_hc)) * exp(c2/2);
% --- Evaluate the roughness sublayer psi_hat functions for momentum and scalars
% These are calculated at the reference height and at the canopy height. Note that
% here the heights are adjusted for the displacement height before the integration.
[psi_m_rsl_zref] = psi_m_rsl (z_minus_d, h_minus_d, x, c1m, c2); % momentum at (zref-disp)
[psi_m_rsl_hc] = psi_m_rsl (h_minus_d, h_minus_d, x, c1m, c2); % momentum at (hc-disp)
[psi_c_rsl_zref] = psi_c_rsl (z_minus_d, h_minus_d, x, c1c, c2); % scalars at (zref-disp)
[psi_c_rsl_hc] = psi_c_rsl (h_minus_d, h_minus_d, x, c1c, c2); % scalars at (hc-disp)
% --- Evaluate the Monin-Obukhov psi functions for momentum and scalars
% These are calculated at the reference height and at the canopy height
[psi_m_zref] = psi_m_monin_obukhov (z_minus_d / x); % momentum at (zref-disp)/obu
[psi_m_hc] = psi_m_monin_obukhov (h_minus_d / x); % momentum at (hc-disp)/obu
[psi_c_zref] = psi_c_monin_obukhov (z_minus_d / x); % scalars at (zref-disp)/obu
[psi_c_hc] = psi_c_monin_obukhov (h_minus_d / x); % scalars at (hc-disp)/obu
% --- Calculate u* (m/s), T* (K), q* (mol/mol), and Tv* (K)
zlog = log(z_minus_d / h_minus_d);
psim = -psi_m_zref + psi_m_hc + psi_m_rsl_zref - psi_m_rsl_hc + physcon.vkc / beta_val;
psic = -psi_c_zref + psi_c_hc + psi_c_rsl_zref - psi_c_rsl_hc + physcon.vkc / beta_val * Pr / f;
fluxvar.ustar = forcvar.uref * physcon.vkc / (zlog + psim);
fluxvar.tstar = (forcvar.thref - fluxvar.tsrf) * physcon.vkc / (zlog + psic);
fluxvar.qstar = (forcvar.eref - fluxvar.esrf) / forcvar.pref * physcon.vkc / (zlog + psic);
tvstar = fluxvar.tstar + 0.61 * forcvar.thref * fluxvar.qstar * (physcon.mmh2o / forcvar.mmair);
% --- Calculate Obukhov length (m)
fluxvar.obu = fluxvar.ustar^2 * forcvar.thvref / (physcon.vkc * physcon.grav * tvstar);
fx = x - fluxvar.obu;
% --- Roughness lengths z0m and z0c (m)
% z0m - Use bisection to find z0m, which lies between aval and bval, and refine the
% estimate until the difference is less than err
aval = surfvar.hc;
bval = 0;
err = 1e-08;
[psi_m_z0m] = psi_m_monin_obukhov (aval / x);
z0m = h_minus_d * exp(-physcon.vkc/beta_val) * exp(-psi_m_hc + psi_m_z0m) * exp(psi_m_rsl_hc);
fa = z0m - aval;
[psi_m_z0m] = psi_m_monin_obukhov (bval / x);
z0m = h_minus_d * exp(-physcon.vkc/beta_val) * exp(-psi_m_hc + psi_m_z0m) * exp(psi_m_rsl_hc);
fb = z0m - bval;
if (fa * fb > 0)
error('RSL bisection error: f(a) and f(b) do not have opposite signs')
end
while (abs(bval-aval) > err)
cval = (aval + bval) / 2;
[psi_m_z0m] = psi_m_monin_obukhov (cval / x);
z0m = h_minus_d * exp(-physcon.vkc/beta_val) * exp(-psi_m_hc + psi_m_z0m) * exp(psi_m_rsl_hc);
fc = z0m - cval;
if (fa * fc < 0)
bval = cval; fb = fc;
else
aval = cval; fa = fc;
end
end
fluxvar.z0m = cval;
% z0c - Use bisection to find z0c, which lies between aval and bval, and refine the
% estimate until the difference is less than err
aval = surfvar.hc;
bval = 0;
[psi_c_z0c] = psi_c_monin_obukhov (aval / x);
z0c = h_minus_d * exp(-physcon.vkc/beta_val*Pr/f) * exp(-psi_c_hc + psi_c_z0c) * exp(psi_c_rsl_hc);
fa = z0c - aval;
[psi_c_z0c] = psi_c_monin_obukhov (bval / x);
z0c = h_minus_d * exp(-physcon.vkc/beta_val*Pr/f) * exp(-psi_c_hc + psi_c_z0c) * exp(psi_c_rsl_hc);
fb = z0c - bval;
if (fa * fb > 0)
error('RSL bisection error: f(a) and f(b) do not have opposite signs')
end
while (abs(bval-aval) > err)
cval = (aval + bval) / 2;
[psi_c_z0c] = psi_c_monin_obukhov (cval / x);
z0c = h_minus_d * exp(-physcon.vkc/beta_val*Pr/f) * exp(-psi_c_hc + psi_c_z0c) * exp(psi_c_rsl_hc);
fc = z0c - cval;
if (fa * fc < 0)
bval = cval; fb = fc;
else
aval = cval; fa = fc;
end
end
fluxvar.z0c = cval;
satvap.m | View on GitHub
function [esat, desat] = satvap (tc)
% Compute saturation vapor pressure and change in saturation vapor pressure
% with respect to temperature. Polynomial approximations are from:
% Flatau et al. (1992) Polynomial fits to saturation vapor pressure.
% Journal of Applied Meteorology 31:1507-1513. Input temperature is Celsius.
% --- For water vapor (temperature range is 0C to 100C)
a0 = 6.11213476; b0 = 0.444017302;
a1 = 0.444007856; b1 = 0.286064092e-01;
a2 = 0.143064234e-01; b2 = 0.794683137e-03;
a3 = 0.264461437e-03; b3 = 0.121211669e-04;
a4 = 0.305903558e-05; b4 = 0.103354611e-06;
a5 = 0.196237241e-07; b5 = 0.404125005e-09;
a6 = 0.892344772e-10; b6 = -0.788037859e-12;
a7 = -0.373208410e-12; b7 = -0.114596802e-13;
a8 = 0.209339997e-15; b8 = 0.381294516e-16;
% --- For ice (temperature range is -75C to 0C)
c0 = 6.11123516; d0 = 0.503277922;
c1 = 0.503109514; d1 = 0.377289173e-01;
c2 = 0.188369801e-01; d2 = 0.126801703e-02;
c3 = 0.420547422e-03; d3 = 0.249468427e-04;
c4 = 0.614396778e-05; d4 = 0.313703411e-06;
c5 = 0.602780717e-07; d5 = 0.257180651e-08;
c6 = 0.387940929e-09; d6 = 0.133268878e-10;
c7 = 0.149436277e-11; d7 = 0.394116744e-13;
c8 = 0.262655803e-14; d8 = 0.498070196e-16;
% --- Limit temperature to -75C to 100C
tc = min(tc, 100);
tc = max(tc, -75);
% --- Saturation vapor pressure (esat, mb) and derivative (desat, mb)
if (tc >= 0)
esat = a0 + tc*(a1 + tc*(a2 + tc*(a3 + tc*(a4 ...
+ tc*(a5 + tc*(a6 + tc*(a7 + tc*a8)))))));
desat = b0 + tc*(b1 + tc*(b2 + tc*(b3 + tc*(b4 ...
+ tc*(b5 + tc*(b6 + tc*(b7 + tc*b8)))))));
else
esat = c0 + tc*(c1 + tc*(c2 + tc*(c3 + tc*(c4 ...
+ tc*(c5 + tc*(c6 + tc*(c7 + tc*c8)))))));
desat = d0 + tc*(d1 + tc*(d2 + tc*(d3 + tc*(d4 ...
+ tc*(d5 + tc*(d6 + tc*(d7 + tc*d8)))))));
end
% --- Convert from mb to Pa
esat = esat * 100;
desat = desat * 100;
soil_temperature.m | View on GitHub
function [soilvar, fluxvar, bucket] = soil_temperature (physcon, soilvar, fluxvar, bucket, dt, f0, df0)
% Use an implicit formulation with the surface boundary condition specified
% as the soil heat flux (W/m2; positive into the soil) to solve for soil
% temperatures at time n+1.
%
% Calculate soil temperatures as:
%
% dT d dT
% cv -- = -- (k --)
% dt dz dz
%
% where: T = temperature (K)
% t = time (s)
% z = depth (m)
% cv = volumetric heat capacity (J/m3/K)
% k = thermal conductivity (W/m/K)
%
% Set up a tridiagonal system of equations to solve for dT at time n+1,
% where the temperature equation for layer i is:
%
% d_i = a_i*[dT_i-1] n+1 + b_i*[dT_i] n+1 + c_i*[dT_i+1] n+1
%
% The energy flux into the soil is specified as a linear function of
% the temperature of the first soil layer T(1) using the equation:
%
% gsoi = f0([T_1] n) + df0 / dT * ([T_1] n+1 - [T_1] n)
%
% where f0 is the surface energy balance evaluated with T(1) at time n
% and df0/dT is the temperature derivative of f0.
%
% If snow is present and the surface temperature is above freezing, reset
% the temperature to freezing and use the residual energy to melt snow.
% ------------------------------------------------------
% Input
% dt ! Time step (s)
% f0 ! Energy flux into soil (W/m2)
% df0 ! Temperature derivative of f0 (W/m2/K)
% physcon.hfus ! Heat of fusion for water at 0 C (J/kg)
% physcon.tfrz ! Freezing point of water (K)
% soilvar.nsoi ! Number of soil layers
% soilvar.z ! Soil depth (m)
% soilvar.z_plus_onehalf ! Soil depth (m) at i+1/2 interface between layers i and i+1
% soilvar.dz ! Soil layer thickness (m)
% soilvar.dz_plus_onehalf ! Thickness (m) between between i and i+1
% soilvar.tk ! Thermal conductivity (W/m/K)
% soilvar.cv ! Heat capacity (J/m3/K)
% bucket.snow_water ! Snow water (kg H2O/m2)
%
% Input/output
% soilvar.tsoi ! Soil temperature (K)
%
% Output
% fluxvar.gsno ! Snow melt energy flux (W/m2)
% bucket.snow_melt ! Snow melt (kg H2O/m2/s)
% ------------------------------------------------------
% --- Save current soil temperature
for i = 1:soilvar.nsoi
tsoi0(i) = soilvar.tsoi(i);
end
% --- Thermal conductivity at interface (W/m/K)
for i = 1:soilvar.nsoi-1
tk_plus_onehalf(i) = soilvar.tk(i) * soilvar.tk(i+1) * (soilvar.z(i)-soilvar.z(i+1)) / ...
(soilvar.tk(i)*(soilvar.z_plus_onehalf(i)-soilvar.z(i+1)) + soilvar.tk(i+1)*(soilvar.z(i)-soilvar.z_plus_onehalf(i)));
end
% --- Set up tridiagonal matrix
% Top soil layer
i = 1;
a(i) = 0;
c(i) = -tk_plus_onehalf(i) / soilvar.dz_plus_onehalf(i);
b(i) = soilvar.cv(i) * soilvar.dz(i) / dt - c(i) - df0;
d(i) = -tk_plus_onehalf(i) * (soilvar.tsoi(i) - soilvar.tsoi(i+1)) / soilvar.dz_plus_onehalf(i) + f0;
% Layers 2 to nsoi-1
for i = 2:soilvar.nsoi-1
a(i) = -tk_plus_onehalf(i-1) / soilvar.dz_plus_onehalf(i-1);
c(i) = -tk_plus_onehalf(i) / soilvar.dz_plus_onehalf(i);
b(i) = soilvar.cv(i) * soilvar.dz(i) / dt - a(i) - c(i);
d(i) = tk_plus_onehalf(i-1) * (soilvar.tsoi(i-1) - soilvar.tsoi(i)) / soilvar.dz_plus_onehalf(i-1) ...
- tk_plus_onehalf(i) * (soilvar.tsoi(i) - soilvar.tsoi(i+1)) / soilvar.dz_plus_onehalf(i);
end
% Bottom soil layer
i = soilvar.nsoi;
a(i) = -tk_plus_onehalf(i-1) / soilvar.dz_plus_onehalf(i-1);
c(i) = 0;
b(i) = soilvar.cv(i) * soilvar.dz(i) / dt - a(i);
d(i) = tk_plus_onehalf(i-1) * (soilvar.tsoi(i-1) - soilvar.tsoi(i)) / soilvar.dz_plus_onehalf(i-1);
% --- Begin tridiagonal solution: forward sweep for layers N to 1
% Bottom soil layer
i = soilvar.nsoi;
e(i) = a(i) / b(i);
f(i) = d(i) / b(i);
% Layers nsoi-1 to 2
for i = soilvar.nsoi-1: -1: 2
den = b(i) - c(i) * e(i+1);
e(i) = a(i) / den;
f(i) = (d(i) - c(i) * f(i+1)) / den;
end
% Complete the tridiagonal solution to get the temperature of the top soil layer
i = 1;
num = d(i) - c(i) * f(i+1);
den = b(i) - c(i) * e(i+1);
tsoi_test = soilvar.tsoi(i) + num / den;
% --- Surface temperature with adjustment for snow melt
% Potential melt rate based on temperature above freezing
potential_snow_melt = max(0, (tsoi_test - physcon.tfrz) * den / physcon.hfus);
% Maximum melt rate is the amount of snow that is present
maximum_snow_melt = bucket.snow_water / dt;
% Cannot melt more snow than is present
bucket.snow_melt = min(maximum_snow_melt, potential_snow_melt);
% Energy flux for snow melt
fluxvar.gsno = bucket.snow_melt * physcon.hfus;
% Update temperature - If there is no snow melt, tsoi(1) = tsoi_test (as above).
% While snow is melting at the potential rate, tsoi(1) = tfrz. If snow melt is
% less than the potential rate, tsoi(1) > tfrz and < tsoi_test.
soilvar.tsoi(i) = soilvar.tsoi(i) + (num - fluxvar.gsno) / den;
dtsoi(i) = soilvar.tsoi(i) - tsoi0(i);
% --- Now complete the tridiagonal solution for layers 2 to N
for i = 2:soilvar.nsoi
dtsoi(i) = f(i) - e(i) * dtsoi(i-1);
soilvar.tsoi(i) = soilvar.tsoi(i) + dtsoi(i);
end
soil_thermal_properties.m | View on GitHub
function [soilvar] = soil_thermal_properties (physcon, soilvar)
% Calculate soil thermal conductivity and heat capacity
% ------------------------------------------------------
% Input
% physcon.hfus ! Heat of fusion for water at 0 C (J/kg)
% physcon.tfrz ! Freezing point of water (K)
% physcon.tkwat ! Thermal conductivity of water (W/m/K)
% physcon.tkice ! Thermal conductivity of ice (W/m/K)
% physcon.cvwat ! Heat capacity of water (J/m3/K)
% physcon.cvice ! Heat capacity of ice (J/m3/K)
% physcon.rhowat ! Density of water (kg/m3)
% physcon.rhoice ! Density of ice (kg/m3)
% soilvar.method ! Use excess heat or apparent heat capacity for phase change
% soilvar.soil_texture ! Soil texture class
% soilvar.sand ! Percent sand
% soilvar.watsat ! Volumetric soil water content at saturation (porosity)
% soilvar.nsoi ! Number of soil layers
% soilvar.dz ! Soil layer thickness (m)
% soilvar.tsoi ! Soil temperature (K)
% soilvar.h2osoi_liq ! Unfrozen water, liquid (kg H2O/m2)
% soilvar.h2osoi_ice ! Frozen water, ice (kg H2O/m2)
%
% Input/output
% soilvar.tk ! Thermal conducitivty (W/m/K)
% soilvar.cv ! Volumetric heat capacity (J/m3/K)
% ------------------------------------------------------
for i = 1:soilvar.nsoi
% --- Soil texture to process
k = soilvar.soil_texture;
% --- Volumetric soil water and ice
watliq = soilvar.h2osoi_liq(i) / (physcon.rhowat * soilvar.dz(i));
watice = soilvar.h2osoi_ice(i) / (physcon.rhoice * soilvar.dz(i));
% Fraction of total volume that is liquid water
fliq = watliq / (watliq + watice);
% Soil water relative to saturation
s = min((watliq + watice)/soilvar.watsat(k), 1);
% --- Dry thermal conductivity (W/m/K) from bulk density (kg/m3)
bd = 2700 * (1 - soilvar.watsat(k));
tkdry = (0.135 * bd + 64.7) / (2700 - 0.947 * bd);
% --- Soil solids thermal conducitivty (W/m/K)
% Thermal conductivity of quartz (W/m/K)
tk_quartz = 7.7;
% Quartz fraction
quartz = soilvar.sand(k) / 100;
% Thermal conductivity of other minerals (W/m/K)
if (quartz > 0.2)
tko = 2;
else
tko = 3;
end
% Thermal conductivity of soil solids (W/m/K)
tksol = tk_quartz^quartz * tko^(1-quartz);
% --- Saturated thermal conductivity (W/m/K) and unfrozen and frozen values
tksat = tksol^(1-soilvar.watsat(k)) * physcon.tkwat^(fliq*soilvar.watsat(k)) * ...
physcon.tkice^(soilvar.watsat(k)-fliq*soilvar.watsat(k));
tksat_u = tksol^(1-soilvar.watsat(k)) * physcon.tkwat^soilvar.watsat(k);
tksat_f = tksol^(1-soilvar.watsat(k)) * physcon.tkice^soilvar.watsat(k);
% --- Kersten number and unfrozen and frozen values
if (soilvar.sand(k) < 50)
ke_u = log10(max(s,0.1)) + 1;
else
ke_u = 0.7 * log10(max(s,0.05)) + 1;
end
ke_f = s;
if (soilvar.tsoi(i) >= physcon.tfrz)
ke = ke_u;
else
ke = ke_f;
end
% --- Thermal conductivity (W/m/K) and unfrozen and frozen values
soilvar.tk(i) = (tksat - tkdry) * ke + tkdry;
tku = (tksat_u - tkdry) * ke_u + tkdry;
tkf = (tksat_f - tkdry) * ke_f + tkdry;
% --- Heat capacity of soil solids (J/m3/K)
cvsol = 1.926e06;
% --- Heat capacity (J/m3/K) and unfrozen and frozen values
soilvar.cv(i) = (1 - soilvar.watsat(k)) * cvsol + physcon.cvwat * watliq + physcon.cvice * watice;
cvu = (1 - soilvar.watsat(k)) * cvsol + physcon.cvwat * (watliq + watice);
cvf = (1 - soilvar.watsat(k)) * cvsol + physcon.cvice * (watliq + watice);
% --- Adjust heat capacity and thermal conductivity if using apparent heat capacity
switch soilvar.method
case 'apparent-heat-capacity'
% Temperature range for freezing and thawing (K)
tinc = 0.5;
% Heat of fusion (J/m3) - This is equivalent to ql = hfus * (h2osoi_liq + h2osoi_ice) / dz
ql = physcon.hfus * (physcon.rhowat * watliq + physcon.rhoice * watice);
% Heat capacity and thermal conductivity
if (soilvar.tsoi(i) > physcon.tfrz+tinc)
soilvar.cv(i) = cvu;
soilvar.tk(i) = tku;
end
if (soilvar.tsoi(i) >= physcon.tfrz-tinc & soilvar.tsoi(i) <= physcon.tfrz+tinc)
soilvar.cv(i) = (cvf + cvu) / 2 + ql / (2 * tinc);
soilvar.tk(i) = tkf + (tku - tkf) * (soilvar.tsoi(i) - physcon.tfrz + tinc) / (2 * tinc);
end
if (soilvar.tsoi(i) < physcon.tfrz-tinc)
soilvar.cv(i) = cvf;
soilvar.tk(i) = tkf;
end
end
end
surface_fluxes.m | View on GitHub
function [fluxvar, soilvar, bucket] = surface_fluxes (physcon, forcvar, surfvar, soilvar, fluxvar, bucket, dt)
% Calculate soil temperatures and surface fluxes. This routine uses the
% current estimate of surface temperature and vapor pressure to solve
% for the Obukhov length. This then provides the aerodynamic conductance,
% which is used in the surface temperature and flux calculation.
% ------------------------------------------------------
% Input
% dt ! Time step (s)
% physcon.tfrz ! Freezing point of water (K)
% physcon.mmh2o ! Molecular mass of water (kg/mol)
% physcon.hvap ! Latent heat of evaporation (J/kg)
% physcon.hsub ! Latent heat of sublimation (J/kg)
% physcon.sigma ! Stefan-Boltzmann constant (W/m2/K4)
% forcvar.thref ! Potential temperature at reference height (K)
% forcvar.uref ! Wind speed at reference height (m/s)
% forcvar.eref ! Vapor pressure at reference height (Pa)
% forcvar.pref ! Atmospheric pressure (Pa)
% forcvar.cpair ! Specific heat of air at constant pressure, at reference height (J/mol/K)
% forcvar.rhomol ! Molar density at reference height (mol/m3)
% surfvar.emiss ! Surface emissivity
% surfvar.gcan ! Canopy conductance (mol/m2/s)
% soilvar.method ! Use excess heat or apparent heat capacity for phase change
% soilvar.nsoi ! Number of soil layers
% soilvar.dz ! Soil layer thickness (m)
% soilvar.cv ! Heat capacity (J/m3/K)
% fluxvar.profiles ! Use MOST or RSL for flux-profiles
% fluxvar.qa ! Radiative forcing (W/m2)
% fluxvar.bucket ! Use bucket model hydrology soil wetness factor
% bucket.snow_water ! Snow water (kg H2O/m2)
% bucket.soil_water ! Soil water (kg H2O/m2)
% bucket.soil_water_max ! Maximum soil water (kg H2O/m2)
% bucket.soil_beta_max ! Soil water at which soil_beta = 1 (fraction of soil_water_max)
%
% Input/output
% fluxvar.tsrf ! Surface temperature (K)
% fluxvar.esrf ! Surface vapor pressure (Pa)
% soilvar.tsoi ! Soil temperature (K)
% soilvar.h2osoi_liq ! Unfrozen water, liquid (kg H2O/m2)
% soilvar.h2osoi_ice ! Frozen water, ice (kg H2O/m2)
%
% Output
% fluxvar.rnet ! Net radiation (W/m2)
% fluxvar.lwrad ! Emitted longwave radiation (W/m2)
% fluxvar.shflx ! Sensible heat flux (W/m2)
% fluxvar.lhflx ! Latent heat flux (W/m2)
% fluxvar.etflx ! Evapotranspiration (mol H2O/m2/s)
% fluxvar.gsoi ! Soil energy flux (W/m2)
% fluxvar.gsno ! Snow melt energy flux (W/m2)
% fluxvar.gam ! Aerodynamic conductance for momentum (mol/m2/s)
% fluxvar.gac ! Aerodynamic conductance for scalars (mol/m2/s)
% soilvar.hfsoi ! Soil phase change energy flux (W/m2)
% bucket.soil_beta ! Soil wetness factor for evapotranspiration (-)
% bucket.snow_melt ! Snow melt (kg H2O/m2/s)
%
% Output from Obukhov length calculation
% fluxvar.ustar ! Friction velocity (m/s)
% fluxvar.tstar ! Temperature scale (K)
% fluxvar.qstar ! Water vapor scale (mol/mol)
% fluxvar.obu ! Obukhov length (m)
% fluxvar.z0m ! RSL only: Roughness length for momentum (m)
% fluxvar.z0c ! RSL only: Roughness length for scalars (m)
% fluxvar.disp ! RSL only: Displacement height (m)
% ------------------------------------------------------
% --- Calculate the Obukhov length
% Calculate the Obukhov length (obu) for the current surface temperature
% and surface vapor pressure using Monin-Obukhov similarity theory or
% Harman & Finnigan (2007, 2008) roughness sublayer (RSL) theory. Use the
% functions "most" or "rsl" to iterate obu until the change in obu is less
% than tol.
obu0 = 100; % Initial estimate for Obukhov length (m)
obu1 = -100; % Initial estimate for Obukhov length (m)
tol = 0.01; % Accuracy tolerance for Obukhov length (m)
switch fluxvar.profiles
case 'MOST' % Use Monin-Obukhov similarity theory
func_name = 'most'; % The function name is "most", in the file most.m
case 'RSL' % Use canopy coupling with roughness sublayer theory
func_name = 'rsl'; % The function name is "rsl", in the file rsl.m
end
% Solve for the Obukhov length
[fluxvar, oburoot] = hybrid_root (func_name, physcon, forcvar, surfvar, fluxvar, obu0, obu1, tol);
% Uncomment this line to use MOST or RSL for neutral conditions
% [fluxvar, dummy] = most (physcon, forcvar, surfvar, fluxvar, -inf);
% [fluxvar, dummy] = rsl (physcon, forcvar, surfvar, fluxvar, -inf);
% --- Aerodynamic conductances for momentum (gam) and scalars (gac) (mol/m2/s)
fluxvar.gam = forcvar.rhomol * fluxvar.ustar * fluxvar.ustar / forcvar.uref;
fluxvar.gac = forcvar.rhomol * fluxvar.ustar * fluxvar.tstar / (forcvar.thref - fluxvar.tsrf);
% --- Calculate soil temperatures
% Save current temperatures
for i = 1:soilvar.nsoi
tsoi0(i) = soilvar.tsoi(i);
end
% Saturation vapor pressure (Pa) and temperature derivative (Pa/K)
[esat, desat] = satvap (fluxvar.tsrf-physcon.tfrz);
% Latent heat of vaporization or sublimation (J/mol)
if (bucket.snow_water > 0)
lambda_val = physcon.hsub; % Latent heat of sublimation (J/kg)
else
lambda_val = physcon.hvap; % Latent heat of vaporization (J/kg)
end
lambda_val = lambda_val * physcon.mmh2o; % J/kg -> J/mol
% Surface conductance for water vapor (mol/m2/s)
gw = 1 / (1/surfvar.gcan + 1/fluxvar.gac);
% Soil wetness factor for evapotranspiration
switch fluxvar.bucket
case 'no_bucket' % No bucket hydrology
bucket.soil_beta = 1;
case 'use_bucket' % Use bucket hydrology
bucket.soil_beta = min(bucket.soil_water/(bucket.soil_beta_max*bucket.soil_water_max), 1);
end
% Emitted longwave radiation (W/m2) and temperature derivative (W/m2/K)
fluxvar.lwrad = surfvar.emiss * physcon.sigma * fluxvar.tsrf^4;
dlwrad = 4 * surfvar.emiss * physcon.sigma * fluxvar.tsrf^3;
% Sensible heat flux (W/m2) and temperature derivative (W/m2/K)
fluxvar.shflx = forcvar.cpair * (fluxvar.tsrf - forcvar.thref) * fluxvar.gac;
dshflx = forcvar.cpair * fluxvar.gac;
% Latent heat flux (W/m2) and temperature derivative (W/m2/K)
fluxvar.lhflx = lambda_val / forcvar.pref * (esat - forcvar.eref) * gw * bucket.soil_beta;
dlhflx = lambda_val / forcvar.pref * desat * gw * bucket.soil_beta;
% Net energy flux into soil (W/m2) and temperature derivative (W/m2/K)
f0 = fluxvar.qa - fluxvar.lwrad - fluxvar.shflx - fluxvar.lhflx;
df0 = -dlwrad - dshflx - dlhflx;
% Update soil temperatures
[soilvar, fluxvar, bucket] = soil_temperature (physcon, soilvar, fluxvar, bucket, dt, f0, df0);
% --- Update surface fluxes for the change in surface temperature
dtsrf = soilvar.tsoi(1) - tsoi0(1);
fluxvar.lwrad = fluxvar.lwrad + dlwrad * dtsrf;
fluxvar.shflx = fluxvar.shflx + dshflx * dtsrf;
fluxvar.lhflx = fluxvar.lhflx + dlhflx * dtsrf;
fluxvar.gsoi = f0 + df0 * dtsrf;
% --- Adjust heat flux into soil for snow melt
fluxvar.gsoi = fluxvar.gsoi - fluxvar.gsno;
% --- Net radiation
fluxvar.rnet = fluxvar.qa - fluxvar.lwrad;
% --- Error check
err = fluxvar.rnet - fluxvar.shflx - fluxvar.lhflx - fluxvar.gsoi - fluxvar.gsno;
if (abs(err) > 1e-06)
fprintf('err = %15.3f\n',err)
fprintf('qa = %15.3f\n',fluxvar.qa)
fprintf('lwrad = %15.3f\n',fluxvar.lwrad)
fprintf('sh = %15.3f\n',fluxvar.shflx)
fprintf('lh = %15.3f\n',fluxvar.lhflx)
fprintf('gsoi = %15.3f\n',fluxvar.gsoi)
fprintf('gsno = %15.3f\n',fluxvar.gsno)
error ('surface temperature error')
end
% --- Evapotranspiration (mol H2O/m2/s)
fluxvar.etflx = fluxvar.lhflx / lambda_val;
% --- Surface vapor pressure is diagnosed from evaporative flux
fluxvar.esrf = (forcvar.eref / forcvar.pref) + fluxvar.etflx / fluxvar.gac; % mol/mol
fluxvar.esrf = fluxvar.esrf * forcvar.pref; % mol/mol -> Pa
% --- Phase change for soil layers undergoing freezing of thawing
switch soilvar.method
case 'apparent-heat-capacity'
% No explicit phase change energy flux. This is included in the heat capacity.
soilvar.hfsoi = 0;
case 'excess-heat'
% Adjust temperatures for phase change. Freeze or melt ice using energy
% excess or deficit needed to change temperature to the freezing point.
% The variable hfsoi is returned as the energy flux from phase change (W/m2).
[soilvar] = phase_change (physcon, soilvar, dt);
end
% --- Check for energy conservation
% Sum change in energy (W/m2)
edif = 0;
for i = 1:soilvar.nsoi
edif = edif + soilvar.cv(i) * soilvar.dz(i) * (soilvar.tsoi(i) - tsoi0(i)) / dt;
end
% Error check
err = edif - fluxvar.gsoi - soilvar.hfsoi;
if (abs(err) > 1e-03)
error ('Soil temperature energy conservation error')
end
% --- Surface temperature is the first soil layer
fluxvar.tsrf = soilvar.tsoi(1);
Output
Figures
Figure 1
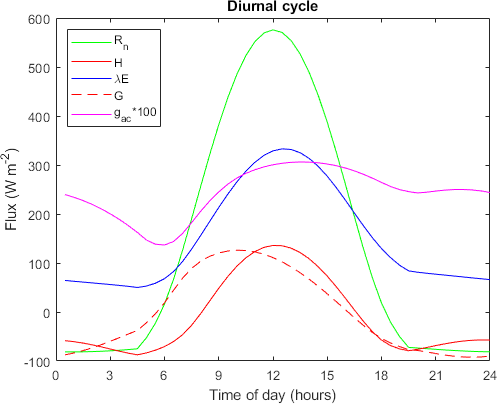
Text
flux.txt | View on GitHub | View raw
hour Ta Ts Rn H LE G ustar gac gcan
0.500 20.381 19.838 -81.492 -58.485 64.330 -87.337 0.616 239.588 25.000
1.000 20.170 19.577 -81.479 -60.586 62.640 -83.533 0.606 234.068 25.000
1.500 20.043 19.380 -81.252 -63.492 60.992 -78.751 0.595 227.380 25.000
2.000 20.000 19.247 -80.805 -67.072 59.366 -73.100 0.581 219.527 25.000
2.500 20.043 19.179 -80.133 -71.154 57.736 -66.716 0.566 210.512 25.000
3.000 20.170 19.173 -79.228 -75.524 56.059 -59.763 0.548 200.328 25.000
3.500 20.381 19.225 -78.079 -79.923 54.279 -52.434 0.528 188.953 25.000
4.000 20.670 19.331 -76.674 -84.036 52.320 -44.958 0.506 176.337 25.000
4.500 21.033 19.482 -74.996 -87.472 50.082 -37.605 0.481 162.382 25.000
5.000 21.464 19.813 -52.546 -83.423 52.892 -22.015 0.452 146.910 27.102
5.500 21.956 20.320 -22.776 -77.953 58.707 -3.530 0.436 138.332 29.813
6.000 22.500 21.025 16.181 -70.598 67.980 18.798 0.433 136.740 32.572
6.500 23.087 21.943 66.712 -60.364 82.554 44.521 0.448 143.854 35.323
7.000 23.706 23.012 125.981 -46.270 103.092 69.160 0.480 160.340 38.001
7.500 24.347 24.134 190.322 -27.034 128.322 89.034 0.521 182.505 40.530
8.000 25.000 25.238 256.366 -3.342 156.171 103.537 0.563 205.571 42.849
8.500 25.653 26.287 321.159 22.558 184.913 113.689 0.601 226.701 44.918
9.000 26.294 27.264 382.182 48.381 213.327 120.474 0.633 245.037 46.712
9.500 26.913 28.158 437.330 72.443 240.459 124.428 0.657 260.902 48.223
10.000 27.500 28.964 484.858 93.425 265.373 126.059 0.673 273.338 49.450
10.500 28.044 29.675 523.372 110.566 287.336 125.470 0.685 282.930 50.397
11.000 28.536 30.284 551.811 123.464 305.647 122.700 0.695 290.422 51.068
11.500 28.967 30.784 569.414 131.901 319.665 117.848 0.702 296.204 51.469
12.000 29.330 31.170 575.718 135.810 328.876 111.031 0.707 300.527 51.602
12.500 29.619 31.437 570.549 135.248 332.924 102.377 0.711 303.564 51.469
13.000 29.830 31.584 554.029 130.358 331.643 92.028 0.713 305.426 51.068
13.500 29.957 31.607 526.573 121.366 325.066 80.141 0.714 306.183 50.397
14.000 30.000 31.508 488.895 108.567 313.437 66.892 0.714 305.875 49.450
14.500 29.957 31.288 442.013 92.329 297.206 52.477 0.713 304.510 48.223
15.000 29.830 30.952 387.267 73.114 277.028 37.124 0.710 302.075 46.712
15.500 29.619 30.503 326.339 51.501 253.742 21.096 0.705 298.541 44.918
16.000 29.330 29.953 261.298 28.231 228.351 4.715 0.699 293.871 42.849
16.500 28.967 29.311 194.655 4.270 201.997 -11.612 0.692 288.035 40.530
17.000 28.536 28.597 129.454 -19.113 175.911 -27.345 0.683 281.050 38.001
17.500 28.044 27.833 69.319 -40.278 151.352 -41.755 0.673 273.055 35.323
18.000 27.500 27.053 18.248 -57.285 129.457 -53.924 0.662 264.452 32.572
18.500 26.913 26.291 -20.797 -68.574 110.934 -63.156 0.651 256.131 29.813
19.000 26.294 25.557 -50.319 -75.250 95.447 -70.516 0.641 249.773 27.102
19.500 25.653 24.844 -72.256 -79.122 83.875 -77.010 0.633 245.638 25.000
20.000 25.000 24.222 -73.497 -76.085 81.137 -78.549 0.628 242.922 25.000
20.500 24.347 23.627 -74.867 -72.399 79.064 -81.532 0.629 244.530 25.000
21.000 23.706 23.049 -76.211 -68.542 77.167 -84.836 0.632 246.804 25.000
21.500 23.087 22.487 -77.459 -64.905 75.300 -87.854 0.635 248.718 25.000
22.000 22.500 21.947 -78.572 -61.767 73.429 -90.235 0.636 249.860 25.000
22.500 21.956 21.437 -79.527 -59.324 71.556 -91.758 0.635 250.034 25.000
23.000 21.464 20.965 -80.306 -57.714 69.694 -92.287 0.633 249.137 25.000
23.500 21.033 20.537 -80.899 -57.020 67.861 -91.740 0.629 247.114 25.000
24.000 20.670 20.159 -81.297 -57.279 66.070 -90.088 0.623 243.936 25.000
sp_07_01_out.txt (standard output) | View on GitHub | View raw
day = 1
day = 2
day = 3
day = 4
day = 5
day = 6
day = 7
day = 8
day = 9
day = 10
day = 11
day = 12
day = 13
day = 14
day = 15
day = 16
day = 17
day = 18
day = 19
day = 20
day = 21
day = 22
day = 23
day = 24
day = 25
day = 26
day = 27
day = 28
day = 29
day = 30
tsoi.txt | View on GitHub | View raw
depth tsoi
-0.009 293.309
-0.031 294.545
-0.068 296.159
-0.128 297.840
-0.227 298.690
-0.391 298.324
-0.661 298.137
-1.106 298.139
-1.840 298.143
-3.049 298.147