Leaf Gas Exchange Coupled with the Leaf Energy Budget
Table of contents
Code
Main program
sp_12_02.m | View on GitHub
% Supplemental program 12.2
% -------------------------------------------------------------------------
% Calculate leaf gas exchange coupled with the leaf energy budget for C3
% and C4 plants. Leaf temperature is calculated from the energy balance.
% -------------------------------------------------------------------------
% --- Waveband indices for visible and near-infrared
params.vis = 1; params.nir = 2;
% --- Physical constants
physcon.grav = 9.80665; % Gravitational acceleration (m/s2)
physcon.tfrz = 273.15; % Freezing point of water (K)
physcon.sigma = 5.67e-08; % Stefan-Boltzmann constant (W/m2/K4)
physcon.mmdry = 28.97 / 1000; % Molecular mass of dry air (kg/mol)
physcon.mmh2o = 18.02 / 1000; % Molecular mass of water (kg/mol)
physcon.cpd = 1005; % Specific heat of dry air at constant pressure (J/kg/K)
physcon.cpw = 1846; % Specific heat of water vapor at constant pressure (J/kg/K)
physcon.rgas = 8.31446; % Universal gas constant (J/K/mol)
physcon.visc0 = 13.3e-06; % Kinematic viscosity at 0C and 1013.25 hPa (m2/s)
physcon.Dh0 = 18.9e-06; % Molecular diffusivity (heat) at 0C and 1013.25 hPa (m2/s)
physcon.Dv0 = 21.8e-06; % Molecular diffusivity (H2O) at 0C and 1013.25 hPa (m2/s)
physcon.Dc0 = 13.8e-06; % Molecular diffusivity (CO2) at 0C and 1013.25 hPa (m2/s)
% --- Set leaf physiology variables
% Stomatal conductance: 0 = Medlyn model. 1 = Ball-Berry model. 2 = WUE optimization
leaf.gstyp = 1;
% Photosynthetic pathway: 1 = C3. 0 = C4
leaf.c3psn = 1;
% Photosynthesis co-limitation: 0 = no. 1 = yes
leaf.colim = 1;
% Leaf physiological parameters
[leaf] = LeafPhysiologyParams (params, physcon, leaf);
% --- Atmospheric forcing
% Process sunlit or shaded leaf
leaftype = 'sun';
% leaftype = 'shade';
% Atmospheric CO2 (umol/mol) and O2 (mmol/mol)
atmos.co2air = 380;
atmos.o2air = 0.209 * 1000;
% Air temperature (K) and relative humidity (%)
atmos.tair = physcon.tfrz + 30;
atmos.relhum = 60;
% Wind (m/s)
% u = 0.01_r8 ! Still air
% u = 0.1_r8 ! Calm - smoke rises vertically
% u = 1.0_r8 ! Light air - smoke drift indicates wind direction
% u = 2.5_r8 ! Light breeze - wind felt on skin, leaves rustle
% u = 5.0_r8 ! Gentle breeze - leaves constantly moving and light flag extended
% u = 10.0_r8 ! Moderate breeze
atmos.wind = 1;
% Atmospheric pressure (Pa)
atmos.patm = 101325;
% Vapor pressure (Pa) and specific humidity (kg/kg)
[esat, desat] = satvap ((atmos.tair-physcon.tfrz));
atmos.eair = esat * (atmos.relhum / 100);
atmos.qair = physcon.mmh2o / physcon.mmdry * atmos.eair / (atmos.patm - (1 - physcon.mmh2o/physcon.mmdry) * atmos.eair);
% Molar density (mol/m3)
atmos.rhomol = atmos.patm / (physcon.rgas * atmos.tair);
% Air density (kg/m3)
atmos.rhoair = atmos.rhomol * physcon.mmdry * (1 - (1 - physcon.mmh2o/physcon.mmdry) * atmos.eair / atmos.patm);
% Molecular mass of air (kg/mol)
atmos.mmair = atmos.rhoair / atmos.rhomol;
% Specific heat of air at constant pressure (J/mol/K)
atmos.cpair = physcon.cpd * (1 + (physcon.cpw/physcon.cpd - 1) * atmos.qair) * atmos.mmair;
% Atmospheric longwave radiation (W/m2)
atmos.irsky = 400;
% Solar radiation (W/m2)
switch leaftype
case 'sun'
fsds = 800; % Sun leaf
case 'shade'
fsds = 300; % Shade leaf
end
atmos.swsky(params.vis) = 0.5 * fsds;
atmos.swsky(params.nir) = 0.5 * fsds;
% --- Ground variables
ground.albsoi(params.vis) = 0.1; % Soil albedo (visible waveband)
ground.albsoi(params.nir) = 0.2; % Soil albedo (near-infrared waveband)
tg = atmos.tair;
ground.irgrd = physcon.sigma * tg^4;
% --- Radiation absorbed by leaf
% Solar radiation incident on leaf
flux.swinc(params.vis) = atmos.swsky(params.vis) * (1 + ground.albsoi(params.vis));
flux.swinc(params.nir) = atmos.swsky(params.nir) * (1 + ground.albsoi(params.nir));
% Solar radiation absorbed by leaf
flux.swflx(params.vis) = flux.swinc(params.vis) * (1 - leaf.rho(params.vis) - leaf.tau(params.vis));
flux.swflx(params.nir) = flux.swinc(params.nir) * (1 - leaf.rho(params.nir) - leaf.tau(params.nir));
flux.apar = flux.swflx(params.vis) * 4.6;
% Radiative forcing for leaf temperature calculation
flux.qa = flux.swflx(params.vis) + flux.swflx(params.nir) + leaf.emiss * (atmos.irsky + ground.irgrd);
% --- Flux calculations for 20 leaves with dleaf = 1 - 20 cm
for p = 1:20
leaf.dleaf = p / 100;
% --- Initial leaf temperature
flux.tleaf = atmos.tair;
% --- Leaf temperature, energy fluxes, photosynthesis, and stomatal conductance
[flux] = LeafFluxes (physcon, atmos, leaf, flux);
% --- Save data for output
x1(p) = leaf.dleaf * 100; % m -> cm
x2(p) = flux.apar;
x3(p) = flux.tleaf - physcon.tfrz; % K -> oC
x4(p) = flux.qa;
x5(p) = flux.lhflx;
x6(p) = flux.etflx * 1000; % mol H2O/m2/s -> mmol H2O/m2/s
x7(p) = flux.an;
x8(p) = flux.an / flux.etflx * 0.001; % mmol CO2 / mol H2O
x9(p) = flux.gbh;
x10(p) = flux.gs;
end
% --- Plot data
plot(x1,x3)
xlabel('Leaf dimension (cm)')
ylabel('Leaf temperature (^{o}C)')
% --- Write data to output file
A = [x1; x2; x3; x4; x5; x6; x7; x8; x9; x10];
filename = 'data.txt';
fileID = fopen(filename,'w');
fprintf(fileID,'%10.3f %10.3f %10.3f %10.3f %10.3f %10.3f %10.3f %10.3f %10.5f %10.5f\n', A);
fclose(fileID);
Aux. programs
brent_root.m | View on GitHub
function [flux, root] = brent_root (func, physcon, atmos, leaf, flux, xa, xb, tol)
% Use Brent's method to find the root of a function, which is known to exist between
% xa and xb. The root is updated until its accuracy is tol. func is the name of the
% function to solve. The variable root is returned as the root of the function. The
% function being evaluated has the definition statement:
%
% function [flux, fx] = func (physcon, atmos, leaf, flux, x)
%
% The function func is exaluated at x and the returned value is fx. It uses variables
% in the physcon, atmos, leaf, and flux structures. These are passed in as
% input arguments. It also calculates values for variables in the flux structure
% so this must be returned in the function call as an output argument. The matlab
% function feval evaluates func.
% --- Evaluate func at xa and xb and make sure the root is bracketed
a = xa;
b = xb;
[flux, fa] = feval(func, physcon, atmos, leaf, flux, a);
[flux, fb] = feval(func, physcon, atmos, leaf, flux, b);
if ((fa > 0 & fb > 0) | (fa < 0 & fb < 0))
error('brent_root error: root must be bracketed')
end
% --- Initialize iteration
itmax = 50; % Maximum number of iterations
eps1 = 1e-08; % Relative error tolerance
c = b;
fc = fb;
% --- Iterative root calculation
for iter = 1:itmax
if ((fb > 0 & fc > 0) | (fb < 0 & fc < 0))
c = a;
fc = fa;
d = b - a;
e = d;
end
if (abs(fc) < abs(fb))
a = b;
b = c;
c = a;
fa = fb;
fb = fc;
fc = fa;
end
tol1 = 2 * eps1 * abs(b) + 0.5 * tol;
xm = 0.5 * (c - b);
% Check to end iteration
if (abs(xm) <= tol1 | fb == 0)
break
end
if (abs(e) >= tol1 & abs(fa) > abs(fb))
s = fb / fa;
if (a == c)
p = 2 * xm * s;
q = 1 - s;
else
q = fa / fc;
r = fb / fc;
p = s * (2 * xm * q * (q - r) - (b - a) * (r - 1));
q = (q - 1) * (r - 1) * (s - 1);
end
if (p > 0)
q = -q;
end
p = abs(p);
if (2*p < min(3*xm*q-abs(tol1*q), abs(e*q)))
e = d;
d = p / q;
else
d = xm;
e = d;
end
else
d = xm;
e = d;
end
a = b;
fa = fb;
if (abs(d) > tol1)
b = b + d;
else
if (xm >= 0)
b = b + abs(tol1);
else
b = b - abs(tol1);
end
end
[flux, fb] = feval(func, physcon, atmos, leaf, flux, b);
% Check to end iteration
if (fb == 0)
break
end
% Check to see if failed to converge
if (iter == itmax)
error('brent_root error: Maximum number of interations exceeded')
end
end
root = b;
CiFunc.m | View on GitHub
function [flux, ci_dif] = CiFunc (physcon, atmos, leaf, flux, ci_val)
% Calculate leaf photosynthesis and stomatal conductance for a specified Ci
% (ci_val). Then calculate a new Ci from the diffusion equation. This function
% returns a value ci_dif = 0 when Ci has converged to the value that satisfies
% the metabolic, stomatal constraint, and diffusion equations.
% ------------------------------------------------------
% Input
% physcon.tfrz ! Freezing point of water (K)
% atmos.o2air ! Atmospheric O2 (mmol/mol)
% atmos.co2air ! Atmospheric CO2 (umol/mol)
% atmos.eair ! Vapor pressure of air (Pa)
% leaf.c3psn ! Photosynthetic pathway: 1 = C3. 0 = C4 plant
% leaf.gstyp ! Stomatal conductance: 0 = Medlyn. 1 = Ball-Berry. 2 = WUE optimization
% leaf.colim ! Photosynthesis co-limitation: 0 = no. 1 = yes
% leaf.colim_c3 ! Empirical curvature parameter for C3 co-limitation
% leaf.colim_c4a ! Empirical curvature parameter for C4 co-limitation
% leaf.colim_c4b ! Empirical curvature parameter for C4 co-limitation
% leaf.qe_c4 ! C4: Quantum yield (mol CO2 / mol photons)
% leaf.g0 ! Ball-Berry minimum leaf conductance (mol H2O/m2/s)
% leaf.g1 ! Ball-Berry slope of conductance-photosynthesis relationship
% flux.vcmax ! Maximum carboxylation rate (umol/m2/s)
% flux.cp ! CO2 compensation point (umol/mol)
% flux.kc ! Michaelis-Menten constant for CO2 (umol/mol)
% flux.ko ! Michaelis-Menten constant for O2 (mmol/mol)
% flux.je ! Electron transport rate (umol/m2/s)
% flux.kp_c4 ! C4: Initial slope of CO2 response curve (mol/m2/s)
% flux.rd ! Leaf respiration rate (umol CO2/m2 leaf/s)
% flux.gbv ! Leaf boundary layer conductance, H2O (mol H2O/m2 leaf/s)
% flux.gbc ! Leaf boundary layer conductance, CO2 (mol CO2/m2 leaf/s)
% flux.apar ! Leaf absorbed PAR (umol photon/m2 leaf/s)
% flux.tleaf ! Leaf temperature (K)
% ci_val ! Input value for Ci (umol/mol)
%
% Output
% flux.ac ! Leaf Rubisco-limited gross photosynthesis (umol CO2/m2 leaf/s)
% flux.aj ! Leaf RuBP regeneration-limited gross photosynthesis (umol CO2/m2 leaf/s)
% flux.ap ! Leaf product-limited (C3) or CO2-limited (C4) gross photosynthesis (umol CO2/m2 leaf/s)
% flux.ag ! Leaf gross photosynthesis (umol CO2/m2 leaf/s)
% flux.an ! Leaf net photosynthesis (umol CO2/m2 leaf/s)
% flux.cs ! Leaf surface CO2 (umol/mol)
% flux.gs ! Leaf stomatal conductance (mol H2O/m2 leaf/s)
% ci_dif ! Difference in Ci
% ------------------------------------------------------
% --- Metabolic (demand-based) photosynthetic rate
if (leaf.c3psn == 1)
% C3: Rubisco-limited photosynthesis
flux.ac = flux.vcmax * max(ci_val - flux.cp, 0) / (ci_val + flux.kc * (1 + atmos.o2air / flux.ko));
% C3: RuBP regeneration-limited photosynthesis
flux.aj = flux.je * max(ci_val - flux.cp, 0) / (4 * ci_val + 8 * flux.cp);
% C3: Product-limited photosynthesis (do not use)
flux.ap = 0;
else
% C4: Rubisco-limited photosynthesis
flux.ac = flux.vcmax;
% C4: RuBP regeneration-limited photosynthesis
flux.aj = leaf.qe_c4 * flux.apar;
% C4: PEP carboxylase-limited (CO2-limited)
flux.ap = flux.kp_c4 * max(ci_val, 0);
end
% --- Net photosynthesis as the minimum or co-limited rate
if (leaf.colim == 1) % Use co-limitation
% First co-limit Ac and Aj. Ai is the intermediate co-limited photosynthesis
% rate found by solving the polynomial: aquad*Ai^2 + bquad*Ai + cquad = 0 for Ai.
% Correct solution is the smallest of the two roots.
if (leaf.c3psn == 1)
aquad = leaf.colim_c3;
else
aquad = leaf.colim_c4a;
end
bquad = -(flux.ac + flux.aj);
cquad = flux.ac * flux.aj;
pcoeff = [aquad bquad cquad];
proots = roots(pcoeff);
ai = min(proots(1), proots(2));
% Now co-limit again using Ap, but only for C4 plants. Solve the polynomial:
% aquad*Ag^2 + bquad*Ag + cquad = 0 for Ag. Correct solution is the smallest
% of the two roots. Ignore the product-limited rate For C3 plants.
if (leaf.c3psn == 0)
aquad = leaf.colim_c4b;
bquad = -(ai + flux.ap);
cquad = ai * flux.ap;
pcoeff = [aquad bquad cquad];
proots = roots(pcoeff);
flux.ag = min(proots(1), proots(2));
else
flux.ag = ai;
end
elseif (leaf.colim == 0) % No co-limitation
if (leaf.c3psn == 1)
flux.ag = min(flux.ac, flux.aj); % C3
else
flux.ag = min(flux.ac, flux.aj, flux.ap); % C4
end
end
% Prevent photosynthesis from ever being negative
flux.ac = max(flux.ac, 0);
flux.aj = max(flux.aj, 0);
flux.ap = max(flux.ap, 0);
flux.ag = max(flux.ag, 0);
% Net CO2 uptake
flux.an = flux.ag - flux.rd;
% --- CO2 at leaf surface
flux.cs = atmos.co2air - flux.an / flux.gbc;
flux.cs = max(flux.cs, 1);
% --- Stomatal constraint function
% Saturation vapor pressure at leaf temperature
[esat, desat] = satvap ((flux.tleaf-physcon.tfrz));
% Ball-Berry stomatal conductance is a quadratic equation
% for gs given An: aquad*gs^2 + bquad*gs + cquad = 0. Correct
% solution is the larger of the two roots. This solution is
% valid for An >= 0. With An <= 0, gs = g0.
if (leaf.gstyp == 1)
term = flux.an / flux.cs;
if (flux.an > 0)
aquad = 1;
bquad = flux.gbv - leaf.g0 - leaf.g1 * term;
cquad = -flux.gbv * (leaf.g0 + leaf.g1 * term * atmos.eair / esat);
pcoeff = [aquad bquad cquad];
proots = roots(pcoeff);
flux.gs = max(proots(1), proots(2));
else
flux.gs = leaf.g0;
end
end
% Quadratic equation for Medlyn stomatal conductance
if (leaf.gstyp == 0)
vpd = max((esat - atmos.eair), 50) * 0.001;
term = 1.6 * flux.an / flux.cs;
if (flux.an > 0)
aquad = 1;
bquad = -(2 * (leaf.g0 + term) + (leaf.g1 * term)^2 / (flux.gbv * vpd));
cquad = leaf.g0 * leaf.g0 + (2 * leaf.g0 + term * (1 - leaf.g1 * leaf.g1 / vpd)) * term;
pcoeff = [aquad bquad cquad];
proots = roots(pcoeff);
flux.gs = max(proots(1), proots(2));
else
flux.gs = leaf.g0;
end
end
% --- Diffusion (supply-based) photosynthetic rate
% Leaf CO2 conductance (mol CO2/m2/s)
gleaf = 1 / (1 / flux.gbc + 1.6 / flux.gs);
% Calculate Ci from the diffusion rate
cinew = atmos.co2air - flux.an / gleaf;
% --- Return the difference between the current Ci and the new Ci
if (flux.an >= 0)
ci_dif = cinew - ci_val;
else
ci_dif = 0;
end
CiFuncOptimization.m | View on GitHub
function [flux] = CiFuncOptimization (atmos, leaf, flux)
% Calculate leaf photosynthesis for a specified stomatal conductance.
% Then calculate Ci from the diffusion equation.
%
% This routine uses a quadratic equation to solve for net photosynthesis (An).
% A general equation for C3 photosynthesis is:
%
% a*(Ci - Cp)
% An = ----------- - Rd
% e*Ci + d
%
% where:
%
% An = Net leaf photosynthesis (umol CO2/m2/s)
% Rd = Leaf respiration (umol CO2/m2/s)
% Ci = Intercellular CO2 concentration (umol/mol)
% Cp = CO2 compensation point (umol/mol)
%
% Rubisco-limited photosynthesis (Ac)
% a = Vcmax
% e = 1
% d = Kc*(1 + Oi/Ko)
%
% RuBP regeneration-limited photosynthesis (Aj)
% a = J
% e = 4
% d = 8*Cp
%
% where:
%
% Vcmax = Maximum carboxylation rate (umol/m2/s)
% Kc = Michaelis-Menten constant for CO2 (umol/mol)
% Ko = Michaelis-Menten constant for O2 (mmol/mol)
% Oi = Intercellular O2 concentration (mmol/mol)
% J = Electron transport rate (umol/m2/s)
%
% Ci is calculated from the diffusion equation:
%
% 1.4 1.6
% An = (Ca - Ci) / (--- + ---)
% gb gs
%
% 1.4 1.6
% Ci = Ca - (--- + ---)*An
% gb gs
%
% where:
%
% Ca = Atmospheric CO2 concentration (umol/mol)
% gb = Leaf boundary layer conductance (mol H2O/m2/s)
% gs = Leaf stomatal conductance (mol H2O/m2/s)
% 1.4 = Corrects gb for the diffusivity of CO2 compared with H2O
% 1.6 = Corrects gs for the diffusivity of CO2 compared with H2O
%
% The resulting quadratic equation is: a*An^2 + b*An + c = 0, which
% is solved for An. Correct solution is the smaller of the two roots.
%
% A similar approach is used for C4 photosynthesis.
% ------------------------------------------------------
% Input
% atmos.o2air ! Atmospheric O2 (mmol/mol)
% atmos.co2air ! Atmospheric CO2 (umol/mol)
% leaf.c3psn ! Photosynthetic pathway: 1 = C3. 0 = C4 plant
% leaf.colim ! Photosynthesis co-limitation: 0 = no. 1 = yes
% leaf.colim_c3 ! Empirical curvature parameter for C3 co-limitation
% leaf.colim_c4a ! Empirical curvature parameter for C4 co-limitation
% leaf.colim_c4b ! Empirical curvature parameter for C4 co-limitation
% leaf.qe_c4 ! C4: Quantum yield (mol CO2 / mol photons)
% flux.vcmax ! Maximum carboxylation rate (umol/m2/s)
% flux.cp ! CO2 compensation point (umol/mol)
% flux.kc ! Michaelis-Menten constant for CO2 (umol/mol)
% flux.ko ! Michaelis-Menten constant for O2 (mmol/mol)
% flux.je ! Electron transport rate (umol/m2/s)
% flux.kp_c4 ! C4: Initial slope of CO2 response curve (mol/m2/s)
% flux.gs ! Leaf stomatal conductance (mol H2O/m2 leaf/s)
% flux.gbc ! Leaf boundary layer conductance, CO2 (mol CO2/m2 leaf/s)
% flux.apar ! Leaf absorbed PAR (umol photon/m2 leaf/s)
% flux.rd ! Leaf respiration rate (umol CO2/m2 leaf/s)
%
% Output
% flux.ac ! Leaf Rubisco-limited gross photosynthesis (umol CO2/m2 leaf/s)
% flux.aj ! Leaf RuBP regeneration-limited gross photosynthesis (umol CO2/m2 leaf/s)
% flux.ap ! Leaf product-limited (C3) or CO2-limited (C4) gross photosynthesis (umol CO2/m2 leaf/s)
% flux.ag ! Leaf gross photosynthesis (umol CO2/m2 leaf/s)
% flux.an ! Leaf net photosynthesis (umol CO2/m2 leaf/s)
% flux.cs ! Leaf surface CO2 (umol/mol)
% flux.ci ! Leaf intercellular CO2 (umol/mol)
% ------------------------------------------------------
% --- Leaf conductance
% gbc has units mol CO2/m2/s
% gs has units mol H2O/m2/s
% gleaf has units mol CO2/m2/s
gleaf = 1 / (1 / flux.gbc + 1.6 / flux.gs);
% --- Gross assimilation rates
if (leaf.c3psn == 1)
% C3: Rubisco-limited photosynthesis
a0 = flux.vcmax;
e0 = 1;
d0 = flux.kc * (1 + atmos.o2air / flux.ko);
aquad = e0 / gleaf;
bquad = -(e0 * atmos.co2air + d0) - (a0 - e0 * flux.rd) / gleaf;
cquad = a0 * (atmos.co2air - flux.cp) - flux.rd * (e0 * atmos.co2air + d0);
pcoeff = [aquad bquad cquad];
proots = roots(pcoeff);
flux.ac = min(proots(1), proots(2)) + flux.rd;
% C3: RuBP regeneration-limited photosynthesis
a0 = flux.je;
e0 = 4;
d0 = 8 * flux.cp;
aquad = e0 / gleaf;
bquad = -(e0 * atmos.co2air + d0) - (a0 - e0 * flux.rd) / gleaf;
cquad = a0 * (atmos.co2air - flux.cp) - flux.rd * (e0 * atmos.co2air + d0);
pcoeff = [aquad bquad cquad];
proots = roots(pcoeff);
flux.aj = min(proots(1), proots(2)) + flux.rd;
% C3: Product-limited photosynthesis
flux.ap = 0;
else
% C4: Rubisco-limited photosynthesis
flux.ac = flux.vcmax;
% C4: RuBP-limited photosynthesis
flux.aj = leaf.qe_c4 * flux.apar;
% C4: PEP carboxylase-limited (CO2-limited)
flux.ap = flux.kp_c4 * (atmos.co2air * gleaf + flux.rd) / (gleaf + flux.kp_c4);
end
% --- Net assimilation as the minimum or co-limited rate
if (leaf.colim == 1) % Use co-limitation
% First co-limit Ac and Aj. Ai is the intermediate co-limited photosynthesis
% rate found by solving the polynomial: aquad*Ai^2 + bquad*Ai + cquad = 0 for Ai.
% Correct solution is the smallest of the two roots.
if (leaf.c3psn == 1)
aquad = leaf.colim_c3;
else
aquad = leaf.colim_c4a;
end
bquad = -(flux.ac + flux.aj);
cquad = flux.ac * flux.aj;
pcoeff = [aquad bquad cquad];
proots = roots(pcoeff);
ai = min(proots(1), proots(2));
% Now co-limit again using Ap, but only for C4 plants. Solve the polynomial:
% aquad*Ag^2 + bquad*Ag + cquad = 0 for Ag. Correct solution is the smallest
% of the two roots. Ignore the product-limited rate For C3 plants.
if (leaf.c3psn == 0)
aquad = leaf.colim_c4b;
bquad = -(ai + flux.ap);
cquad = ai * flux.ap;
pcoeff = [aquad bquad cquad];
proots = roots(pcoeff);
flux.ag = min(proots(1), proots(2));
else
flux.ag = ai;
end
elseif (leaf.colim == 0) % No co-limitation
if (leaf.c3psn == 1)
flux.ag = min(flux.ac, flux.aj); % C3
else
flux.ag = min(flux.ac, flux.aj, flux.ap); % C4
end
end
% Prevent photosynthesis from ever being negative
flux.ac = max(flux.ac, 0);
flux.aj = max(flux.aj, 0);
flux.ap = max(flux.ap, 0);
flux.ag = max(flux.ag, 0);
% Net CO2 uptake
flux.an = flux.ag - flux.rd;
% --- CO2 at leaf surface
flux.cs = atmos.co2air - flux.an / flux.gbc;
flux.cs = max(flux.cs, 1);
% --- Intercelluar CO2
flux.ci = atmos.co2air - flux.an / gleaf;
hybrid_root.m | View on GitHub
function [flux, root] = hybrid_root (func, physcon, atmos, leaf, flux, xa, xb, tol)
% Solve for the root of a function using the secant and Brent's methods given
% initial estimates xa and xb. The root is updated until its accuracy is tol.
% func is the name of the function to solve. The variable root is returned as
% the root of the function. The function being evaluated has the definition statement:
%
% function [flux, fx] = func (physcon, atmos, leaf, flux, x)
%
% The function func is exaluated at x and the returned value is fx. It uses variables
% in the physcon, atmos, leaf, and flux structures. These are passed in as
% input arguments. It also calculates values for variables in the flux structure
% so this must be returned in the function call as an output argument. The matlab
% function feval evaluates func.
% --- Evaluate func at xa and see if this is the root
x0 = xa;
[flux, f0] = feval(func, physcon, atmos, leaf, flux, x0);
if (f0 == 0)
root = x0;
return
end
% --- Evaluate func at xb and see if this is the root
x1 = xb;
[flux, f1] = feval(func, physcon, atmos, leaf, flux, x1);
if (f1 == 0)
root = x1;
return
end
% --- Order initial root estimates correctly
if (f1 < f0)
minx = x1;
minf = f1;
else
minx = x0;
minf = f0;
end
% --- Iterative root calculation. Use the secant method, with Brent's method as a backup
itmax = 40;
for iter = 1:itmax
dx = -f1 * (x1 - x0) / (f1 - f0);
x = x1 + dx;
% Check if x is the root. If so, exit the iteration
if (abs(dx) < tol)
x0 = x;
break
end
% Evaluate the function at x
x0 = x1;
f0 = f1;
x1 = x;
[flux, f1] = feval(func, physcon, atmos, leaf, flux, x1);
if (f1 < minf)
minx = x1;
minf = f1;
end
% If a root zone is found, use Brent's method for a robust backup strategy
% and exit the iteration
if (f1 * f0 < 0)
[flux, x] = brent_root (func, physcon, atmos, leaf, flux, x0, x1, tol);
x0 = x;
break
end
% In case of failing to converge within itmax iterations stop at the minimum function
if (iter == itmax)
[flux, f1] = feval(func, physcon, atmos, leaf, flux, minx);
x0 = minx;
end
end
root = x0;
latvap.m | View on GitHub
function [val] = latvap (tc, mmh2o)
% Latent heat of vaporization (J/mol) at temperature tc (degC)
val = 2501.6 - 2.3773 * tc; % Latent heat of vaporization (J/g)
val = val * 1000; % Convert from J/g to J/kg
val = val * mmh2o; % Convert from J/kg to J/mol
LeafBoundaryLayer.m | View on GitHub
function [flux] = LeafBoundaryLayer (physcon, atmos, leaf, flux)
% Leaf boundary layer conductances
% -------------------------------------------------------------------------
% Input
% physcon.grav ! Gravitational acceleration (m/s2)
% physcon.tfrz ! Freezing point of water (K)
% physcon.visc0 ! Kinematic viscosity at 0C and 1013.25 hPa (m2/s)
% physcon.Dh0 ! Molecular diffusivity (heat) at 0C and 1013.25 hPa (m2/s)
% physcon.Dv0 ! Molecular diffusivity (H2O) at 0C and 1013.25 hPa (m2/s)
% physcon.Dc0 ! Molecular diffusivity (CO2) at 0C and 1013.25 hPa (m2/s)
% atmos.patm ! Atmospheric pressure (Pa)
% atmos.rhomol ! Molar density mol/m3)
% atmos.wind ! Wind speed (m/s)
% atmos.tair ! Air temperature (K)
% leaf.dleaf ! Leaf dimension (m)
% flux.tleaf ! Leaf temperature (K)
%
% Output
% flux.gbh ! Leaf boundary layer conductance, heat (mol/m2 leaf/s)
% flux.gbv ! Leaf boundary layer conductance, H2O (mol H2O/m2 leaf/s)
% flux.gbc ! Leaf boundary layer conductance, CO2 (mol CO2/m2 leaf/s)
% -------------------------------------------------------------------------
% --- Adjust diffusivity for temperature and pressure
fac = 101325 / atmos.patm * (atmos.tair / physcon.tfrz)^1.81;
visc = physcon.visc0 * fac; % Kinematic viscosity (m2/s)
Dh = physcon.Dh0 * fac; % Molecular diffusivity, heat (m2/s)
Dv = physcon.Dv0 * fac; % Molecular diffusivity, H2O (m2/s)
Dc = physcon.Dc0 * fac; % Molecular diffusivity, CO2 (m2/s)
% --- Dimensionless numbers
Re = atmos.wind * leaf.dleaf / visc; % Reynolds number
Pr = visc / Dh; % Prandtl number
Scv = visc / Dv; % Schmidt number for H2O
Scc = visc / Dc; % Schmidt number for CO2
% Grashof number
Gr = physcon.grav * leaf.dleaf^3 * max(flux.tleaf-atmos.tair, 0) / (atmos.tair * visc * visc);
% --- Empirical correction factor for Nu and Sh
b1 = 1.5;
% --- Nusselt number (Nu) and Sherwood numbers (H2O: Shv, CO2: Shc)
% Forced convection - laminar flow
Nu_lam = b1 * 0.66 * Pr^0.33 * Re^0.5; % Nusselt number
Shv_lam = b1 * 0.66 * Scv^0.33 * Re^0.5; % Sherwood number, H2O
Shc_lam = b1 * 0.66 * Scc^0.33 * Re^0.5; % Sherwood number, CO2
% Forced convection - turbulent flow
Nu_turb = b1 * 0.036 * Pr^0.33 * Re^0.8; % Nusselt number
Shv_turb = b1 * 0.036 * Scv^0.33 * Re^0.8; % Sherwood number, H2O
Shc_turb = b1 * 0.036 * Scc^0.33 * Re^0.8; % Sherwood number, CO2
% Choose correct flow regime for forced convection
Nu_forced = max(Nu_lam, Nu_turb);
Shv_forced = max(Shv_lam, Shv_turb);
Shc_forced = max(Shc_lam, Shc_turb);
% Free convection
Nu_free = 0.54 * Pr^0.25 * Gr^0.25; % Nusselt number
Shv_free = 0.54 * Scv^0.25 * Gr^0.25; % Sherwood number, H2O
Shc_free = 0.54 * Scc^0.25 * Gr^0.25; % Sherwood number, CO2
% Both forced and free convection regimes occur together
Nu = Nu_forced + Nu_free;
Shv = Shv_forced + Shv_free;
Shc = Shc_forced + Shc_free;
% --- Boundary layer conductances (m/s)
flux.gbh = Dh * Nu / leaf.dleaf;
flux.gbv = Dv * Shv / leaf.dleaf;
flux.gbc = Dc * Shc / leaf.dleaf;
% --- Convert conductance (m/s) to (mol/m2/s)
flux.gbh = flux.gbh * atmos.rhomol;
flux.gbv = flux.gbv * atmos.rhomol;
flux.gbc = flux.gbc * atmos.rhomol;
LeafFluxes.m | View on GitHub
function [flux] = LeafFluxes (physcon, atmos, leaf, flux)
% --- Leaf temperature, energy fluxes, photosynthesis, and stomatal conductance
if (leaf.gstyp <= 1)
% Solve for tleaf: Use TleafFunc to iterate leaf temperature, energy fluxes,
% photosynthesis and stomatal conductance. This temperature is refined to an
% accuracy of tol. Do not use the returned value (dummy), and instead use
% the tleaf calculated in the final call to TleafFunc.
t0 = flux.tleaf - 1.0; % Initial estimate for leaf temperature (K)
t1 = flux.tleaf + 1.0; % Initial estimate for leaf temperature (K)
tol = 0.1; % Accuracy tolerance for tleaf (K)
func_name = 'TleafFunc'; % The function name
[flux, dummy] = hybrid_root (func_name, physcon, atmos, leaf, flux, t0, t1, tol);
elseif (leaf.gstyp == 2)
% Iterate leaf temperature, flux calculations, and stomatal conductance
% using stomatal optimization
[flux] = StomataOptimization (physcon, atmos, leaf, flux);
end
LeafPhotosynthesis.m | View on GitHub
function [flux] = LeafPhotosynthesis (physcon, atmos, leaf, flux)
% Calculate leaf photosynthesis using one of two methods:
% (1) Calculate leaf photosynthesis and stomatal conductance
% by solving for the value of Ci that satisfies the
% metabolic, stomatal constraint, and diffusion equations.
% This is used with the Ball-Berry style stomatal models.
% (2) Calculate leaf photosynthesis for a specified stomatal
% conductance. Then calculate Ci from the diffusion equation.
% This is used with the WUE stomatal optimization.
% ------------------------------------------------------
% Input
% physcon.tfrz ! Freezing point of water (K)
% physcon.rgas ! Universal gas constant (J/K/mol)
% atmos.co2air ! Atmospheric CO2 (umol/mol)
% atmos.eair ! Vapor pressure of air (Pa)
% leaf.gstyp ! Stomatal conductance: 0 = Medlyn. 1 = Ball-Berry. 2 = WUE optimization
% leaf.c3psn ! Photosynthetic pathway: 1 = C3. 0 = C4 plant
% leaf.vcmax25 ! Maximum carboxylation rate at 25C (umol/m2/s)
% leaf.jmax25 ! Maximum electron transport rate at 25C (umol/m2/s)
% leaf.rd25 ! Leaf respiration rate at 25C (umol CO2/m2/s)
% leaf.kc25 ! Michaelis-Menten constant for CO2 at 25C (umol/mol)
% leaf.ko25 ! Michaelis-Menten constant for O2 at 25C (mmol/mol)
% leaf.cp25 ! CO2 compensation point at 25C (umol/mol)
% leaf.kcha ! Activation energy for Kc (J/mol)
% leaf.koha ! Activation energy for Ko (J/mol)
% leaf.cpha ! Activation energy for Cp (J/mol)
% leaf.vcmaxha ! Activation energy for Vcmax (J/mol)
% leaf.jmaxha ! Activation energy for Jmax (J/mol)
% leaf.rdha ! Activation energy for Rd (J/mol)
% leaf.vcmaxhd ! Deactivation energy for Vcmax (J/mol)
% leaf.jmaxhd ! Deactivation energy for Jmax (J/mol)
% leaf.rdhd ! Deactivation energy for Rd (J/mol)
% leaf.vcmaxse ! Entropy term for Vcmax (J/mol/K)
% leaf.jmaxse ! Entropy term for Jmax (J/mol/K)
% leaf.rdse ! Entropy term for Rd (J/mol/K)
% leaf.vcmaxc ! Vcmax scaling factor for high temperature inhibition (25 C = 1.0)
% leaf.jmaxc ! Jmax scaling factor for high temperature inhibition (25 C = 1.0)
% leaf.rdc ! Rd scaling factor for high temperature inhibition (25 C = 1.0)
% leaf.phi_psii ! Quantum yield of PS II
% leaf.theta_j ! Empirical curvature parameter for electron transport rate
% leaf.kp25_c4 ! C4: Initial slope of CO2 response curve at 25C (mol/m2/s)
% leaf.g0 ! Ball-Berry minimum leaf conductance (mol H2O/m2/s)
% leaf.g1 ! Ball-Berry slope of conductance-photosynthesis relationship
% flux.gbv ! Leaf boundary layer conductance, H2O (mol H2O/m2 leaf/s)
% flux.gbc ! Leaf boundary layer conductance, CO2 (mol CO2/m2 leaf/s)
% flux.apar ! Leaf absorbed PAR (umol photon/m2 leaf/s)
% flux.tleaf ! Leaf temperature (K)
%
% Input or output (depending on method)
% flux.gs ! Leaf stomatal conductance (mol H2O/m2 leaf/s)
%
% Output
% flux.vcmax ! Maximum carboxylation rate (umol/m2/s)
% flux.jmax ! Maximum electron transport rate (umol/m2/s)
% flux.cp ! CO2 compensation point (umol/mol)
% flux.kc ! Michaelis-Menten constant for CO2 (umol/mol)
% flux.ko ! Michaelis-Menten constant for O2 (mmol/mol)
% flux.je ! Electron transport rate (umol/m2/s)
% flux.kp_c4 ! C4: Initial slope of CO2 response curve (mol/m2/s)
% flux.ac ! Leaf Rubisco-limited gross photosynthesis (umol CO2/m2 leaf/s)
% flux.aj ! Leaf RuBP regeneration-limited gross photosynthesis (umol CO2/m2 leaf/s)
% flux.ap ! Leaf product-limited (C3) or CO2-limited (C4) gross photosynthesis (umol CO2/m2 leaf/s)
% flux.ag ! Leaf gross photosynthesis (umol CO2/m2 leaf/s)
% flux.an ! Leaf net photosynthesis (umol CO2/m2 leaf/s)
% flux.rd ! Leaf respiration rate (umol CO2/m2 leaf/s)
% flux.cs ! Leaf surface CO2 (umol/mol)
% flux.ci ! Leaf intercellular CO2 (umol/mol)
% flux.hs ! Leaf fractional humidity at surface (dimensionless)
% flux.vpd ! Leaf vapor pressure deficit at surface (Pa)
% ------------------------------------------------------
% --- Adjust photosynthetic parameters for temperature
if (leaf.c3psn == 1)
% C3 temperature response
ft = @(tl, ha) exp(ha/(physcon.rgas*(physcon.tfrz+25)) * (1-(physcon.tfrz+25)/tl));
fth = @(tl, hd, se, fc) fc / (1 + exp((-hd+se*tl)/(physcon.rgas*tl)));
flux.kc = leaf.kc25 * ft(flux.tleaf, leaf.kcha);
flux.ko = leaf.ko25 * ft(flux.tleaf, leaf.koha);
flux.cp = leaf.cp25 * ft(flux.tleaf, leaf.cpha);
t1 = ft(flux.tleaf, leaf.vcmaxha);
t2 = fth(flux.tleaf, leaf.vcmaxhd, leaf.vcmaxse, leaf.vcmaxc);
flux.vcmax = leaf.vcmax25 * t1 * t2;
t1 = ft(flux.tleaf, leaf.jmaxha);
t2 = fth(flux.tleaf, leaf.jmaxhd, leaf.jmaxse, leaf.jmaxc);
flux.jmax = leaf.jmax25 * t1 * t2;
t1 = ft(flux.tleaf, leaf.rdha);
t2 = fth(flux.tleaf, leaf.rdhd, leaf.rdse, leaf.rdc);
flux.rd = leaf.rd25 * t1 * t2;
flux.kp_c4 = 0;
elseif (leaf.c3psn == 0)
% C4 temperature response
t1 = 2^((flux.tleaf-(physcon.tfrz+25)) / 10);
t2 = 1 + exp(0.2*((physcon.tfrz+15)-flux.tleaf));
t3 = 1 + exp(0.3*(flux.tleaf-(physcon.tfrz+40)));
flux.vcmax = leaf.vcmax25 * t1 / (t2 * t3);
t3 = 1 + exp(1.3*(flux.tleaf-(physcon.tfrz+55)));
flux.rd = leaf.rd25 * t1 / t3;
flux.kp_c4 = leaf.kp25_c4 * t1;
flux.kc = 0;
flux.ko = 0;
flux.cp = 0;
flux.jmax = 0;
flux.je = 0;
end
% --- Electron transport rate for C3 plants
% Solve the polynomial: aquad*Je^2 + bquad*Je + cquad = 0
% for Je. Correct solution is the smallest of the two roots.
if (leaf.c3psn == 1)
qabs = 0.5 * leaf.phi_psii * flux.apar;
aquad = leaf.theta_j;
bquad = -(qabs + flux.jmax);
cquad = qabs * flux.jmax;
pcoeff = [aquad bquad cquad];
proots = roots(pcoeff);
flux.je = min(proots(1), proots(2));
end
% --- Ci calculation
if (leaf.gstyp <= 1)
% Initial estimates for Ci
if (leaf.c3psn == 1)
ci0 = 0.7 * atmos.co2air;
elseif (leaf.c3psn == 0)
ci0 = 0.4 * atmos.co2air;
end
ci1 = ci0 * 0.99;
% Solve for Ci: Use CiFunc to iterate photosynthesis calculations
% until the change in Ci is < tol. Ci has units umol/mol
tol = 0.1; % Accuracy tolerance for Ci (umol/mol)
func_name = 'CiFunc'; % The function name
[flux, dummy] = hybrid_root (func_name, physcon, atmos, leaf, flux, ci0, ci1, tol);
flux.ci = dummy;
elseif (leaf.gstyp == 2)
% Calculate photosynthesis for a specified stomatal conductance
[flux] = CiFuncOptimization (atmos, leaf, flux);
end
% --- Relative humidity and vapor pressure at leaf surface
[esat, desat] = satvap ((flux.tleaf-physcon.tfrz));
flux.hs = (flux.gbv * atmos.eair + flux.gs * esat) / ((flux.gbv + flux.gs) * esat);
flux.vpd = max(esat - flux.hs*esat, 0.1);
% --- Make sure iterative solution is correct
if (flux.gs < 0)
error ('LeafPhotosynthesis: negative stomatal conductance')
end
% Compare with Ball-Berry model. The solution blows up with low eair. In input
% data, eair should be > 0.05*esat to ensure that hs does not go to zero.
if (leaf.gstyp == 1)
gs_err = leaf.g1 * max(flux.an, 0) * flux.hs / flux.cs + leaf.g0;
if (abs(flux.gs-gs_err)*1e06 > 1e-04)
fprintf('gs = %15.4f\n', flux.gs)
fprintf('gs_err = %15.4f\n', gs_err)
error ('LeafPhotosynthesis: failed Ball-Berry error check')
end
end
% Compare with Medlyn model. The solutions blows up with vpd = 0. The
% quadratic calcuation of gsw in CiFunc constrains vpd > 50 Pa, so this
% comparison is only valid for those conditions.
if (leaf.gstyp == 0)
if ((esat - atmos.eair) > 50)
gs_err = 1.6 * (1 + leaf.g1 / sqrt(flux.vpd*0.001)) * max(flux.an, 0) / flux.cs + leaf.g0;
if (abs(flux.gs-gs_err)*1e06 > 1e-04)
fprintf('gs = %15.4f\n', flux.gs)
fprintf('gs_err = %15.4f\n', gs_err)
error ('LeafPhotosynthesis: failed Medlyn error check')
end
end
end
% Compare with diffusion equation: An = (ca - ci) * gleaf
an_err = (atmos.co2air - flux.ci) / (1 / flux.gbc + 1.6 / flux.gs);
if (flux.an > 0 & abs(flux.an-an_err) > 0.01)
fprintf('An = %15.4f\n', flux.an)
fprintf('An_err = %15.4f\n', an_err)
error ('LeafPhotosynthesis: failed diffusion error check')
end
LeafPhysiologyParams.m | View on GitHub
function [leaf] = LeafPhysiologyParams (params, physcon, leaf)
% ------------------------------------------------------
% Input
% params.vis ! Waveband index for visible radiation
% params.nir ! Waveband index for near-infrared radiation
% physcon.tfrz ! Freezing point of water (K)
% physcon.rgas ! Universal gas constant (J/K/mol)
% leaf.c3psn ! Photosynthetic pathway: 1 = C3. 0 = C4 plant
% leaf.gstyp ! Stomatal conductance: 0 = Medlyn. 1 = Ball-Berry. 2 = WUE optimization
%
% Output
% leaf.vcmax25 ! Maximum carboxylation rate at 25C (umol/m2/s)
% leaf.jmax25 ! Maximum electron transport rate at 25C (umol/m2/s)
% leaf.rd25 ! Leaf respiration rate at 25C (umol CO2/m2/s)
% leaf.kc25 ! Michaelis-Menten constant for CO2 at 25C (umol/mol)
% leaf.ko25 ! Michaelis-Menten constant for O2 at 25C (mmol/mol)
% leaf.cp25 ! CO2 compensation point at 25C (umol/mol)
% leaf.kcha ! Activation energy for Kc (J/mol)
% leaf.koha ! Activation energy for Ko (J/mol)
% leaf.cpha ! Activation energy for Cp (J/mol)
% leaf.vcmaxha ! Activation energy for Vcmax (J/mol)
% leaf.jmaxha ! Activation energy for Jmax (J/mol)
% leaf.rdha ! Activation energy for Rd (J/mol)
% leaf.vcmaxhd ! Deactivation energy for Vcmax (J/mol)
% leaf.jmaxhd ! Deactivation energy for Jmax (J/mol)
% leaf.rdhd ! Deactivation energy for Rd (J/mol)
% leaf.vcmaxse ! Entropy term for Vcmax (J/mol/K)
% leaf.jmaxse ! Entropy term for Jmax (J/mol/K)
% leaf.rdse ! Entropy term for Rd (J/mol/K)
% leaf.vcmaxc ! Vcmax scaling factor for high temperature inhibition (25 C = 1.0)
% leaf.jmaxc ! Jmax scaling factor for high temperature inhibition (25 C = 1.0)
% leaf.rdc ! Rd scaling factor for high temperature inhibition (25 C = 1.0)
% leaf.phi_psii ! Quantum yield of PS II
% leaf.theta_j ! Empirical curvature parameter for electron transport rate
% leaf.colim_c3 ! Empirical curvature parameter for C3 co-limitation
% leaf.colim_c4a ! Empirical curvature parameter for C4 co-limitation
% leaf.colim_c4b ! Empirical curvature parameter for C4 co-limitation
% leaf.qe_c4 ! C4: Quantum yield (mol CO2 / mol photons)
% leaf.kp25_c4 ! C4: Initial slope of CO2 response curve at 25C (mol/m2/s)
% leaf.g0 ! Minimum leaf conductance (mol H2O/m2/s)
% leaf.g1 ! Slope of conductance-photosynthesis relationship
% leaf.dleaf ! Leaf dimension (m)
% leaf.emiss ! Leaf emissivity
% leaf.rho ! Leaf reflectance for visible (vis) and near-infrared (nir) wavebands
% leaf.tau ! Leaf transmittance for visible (vis) and near-infrared (nir) wavebands
% leaf.iota ! Stomatal efficiency (umol CO2/ mol H2O)
% ------------------------------------------------------
% --- Vcmax and other parameters (at 25C)
if (leaf.c3psn == 1)
leaf.vcmax25 = 60;
leaf.jmax25 = 1.67 * leaf.vcmax25;
leaf.kp25_c4 = 0;
leaf.rd25 = 0.015 * leaf.vcmax25;
else
leaf.vcmax25 = 40;
leaf.jmax25 = 0;
leaf.kp25_c4 = 0.02 * leaf.vcmax25;
leaf.rd25 = 0.025 * leaf.vcmax25;
end
% --- Kc, Ko, Cp at 25C
leaf.kc25 = 404.9;
leaf.ko25 = 278.4;
leaf.cp25 = 42.75;
% --- Activation energy
leaf.kcha = 79430;
leaf.koha = 36380;
leaf.cpha = 37830;
leaf.rdha = 46390;
leaf.vcmaxha = 65330;
leaf.jmaxha = 43540;
% --- High temperature deactivation
% Deactivation energy (J/mol)
leaf.rdhd = 150000;
leaf.vcmaxhd = 150000;
leaf.jmaxhd = 150000;
% Entropy term (J/mol/K)
leaf.rdse = 490;
leaf.vcmaxse = 490;
leaf.jmaxse = 490;
% Scaling factors for high temperature inhibition (25 C = 1.0).
% The factor "c" scales the deactivation to a value of 1.0 at 25C.
fth25 = @(hd, se) 1 + exp((-hd + se*(physcon.tfrz+25)) / (physcon.rgas*(physcon.tfrz+25)));
leaf.vcmaxc = fth25 (leaf.vcmaxhd, leaf.vcmaxse);
leaf.jmaxc = fth25 (leaf.jmaxhd, leaf.jmaxse);
leaf.rdc = fth25 (leaf.rdhd, leaf.rdse);
% --- C3 parameters
% Quantum yield of PS II
leaf.phi_psii = 0.85;
% Empirical curvature parameter for electron transport rate
leaf.theta_j = 0.90;
% Empirical curvature parameter for C3 co-limitation
leaf.colim_c3 = 0.98;
% Empirical curvature parameters for C4 co-limitation
leaf.colim_c4a = 0.80;
leaf.colim_c4b = 0.95;
% --- C4: Quantum yield (mol CO2 / mol photons)
leaf.qe_c4 = 0.05;
% --- Stomatal conductance parameters
if (leaf.c3psn == 1)
if (leaf.gstyp == 1)
leaf.g0 = 0.01; % Ball-Berry minimum leaf conductance (mol H2O/m2/s)
leaf.g1 = 9.0; % Ball-Berry slope of conductance-photosynthesis relationship
elseif (leaf.gstyp == 0)
leaf.g0 = 0.0; % Medlyn minimum leaf conductance (mol H2O/m2/s)
leaf.g1 = 4.45; % Medlyn slope of conductance-photosynthesis relationship
end
else
if (leaf.gstyp == 1)
leaf.g0 = 0.04; % Ball-Berry minimum leaf conductance (mol H2O/m2/s)
leaf.g1 = 4.0; % Ball-Berry slope of conductance-photosynthesis relationship
elseif (leaf.gstyp == 0)
leaf.g0 = 0.0; % Medlyn minimum leaf conductance (mol H2O/m2/s)
leaf.g1 = 1.62; % Medlyn slope of conductance-photosynthesis relationship
end
end
% --- Stomatal efficiency for optimization (An/E; umol CO2/ mol H2O)
if (leaf.gstyp == 2)
leaf.iota = 750;
end
% --- Leaf dimension (m)
leaf.dleaf = 0.05;
% --- Leaf emissivity
leaf.emiss = 0.98;
% --- Leaf reflectance and transmittance: visible and near-infrared wavebands
leaf.rho(params.vis) = 0.10;
leaf.tau(params.vis) = 0.10;
leaf.rho(params.nir) = 0.40;
leaf.tau(params.nir) = 0.40;
LeafTemperature.m | View on GitHub
function [flux] = LeafTemperature (physcon, atmos, leaf, flux)
% Leaf temperature and energy fluxes
% ------------------------------------------------------
% Input
% physcon.tfrz ! Freezing point of water (K)
% physcon.mmh2o ! Molecular mass of water (kg/mol)
% physcon.sigma ! Stefan-Boltzmann constant (W/m2/K4)
% atmos.patm ! Atmospheric pressure (Pa)
% atmos.cpair ! Specific heat of air at constant pressure (J/mol/K)
% atmos.tair ! Air temperature (K)
% atmos.eair ! Vapor pressure of air (Pa)
% leaf.emiss ! Leaf emissivity
% flux.gbh ! Leaf boundary layer conductance, heat (mol/m2 leaf/s)
% flux.gbv ! Leaf boundary layer conductance, H2O (mol H2O/m2 leaf/s)
% flux.gs ! Leaf stomatal conductance (mol H2O/m2 leaf/s)
% flux.qa ! Leaf radiative forcing (W/m2 leaf)
%
% Input/ouput
% flux.tleaf ! Leaf temperature (K)
%
% Output
% flux.rnet ! Leaf net radiation (W/m2 leaf)
% flux.lwrad ! Longwave radiation emitted from leaf (W/m2 leaf)
% flux.shflx ! Leaf sensible heat flux (W/m2 leaf)
% flux.lhflx ! Leaf latent heat flux (W/m2 leaf)
% flux.etflx ! Leaf transpiration flux (mol H2O/m2 leaf/s)
% ------------------------------------------------------
% --- Latent heat of vaporization (J/mol)
[lambda_val] = latvap ((atmos.tair-physcon.tfrz), physcon.mmh2o);
% --- Newton-Raphson iteration until leaf energy balance is less than
% f0_max or to niter_max iterations
niter = 0; % Number of iterations
f0 = 1e36; % Leaf energy balance (W/m2)
niter_max = 100; % Maximum number of iterations
f0_max = 1e-06; % Maximum energy imbalance (W/m2)
while (niter <= niter_max & abs(f0) > f0_max)
% Increment iteration counter
niter = niter + 1;
% Saturation vapor pressure (Pa) and temperature derivative (Pa/K)
[esat, desat] = satvap ((flux.tleaf-physcon.tfrz));
% Leaf conductance for water vapor (mol H2O/m2/s)
gleaf = flux.gs * flux.gbv / (flux.gs + flux.gbv);
% Emitted longwave radiation (W/m2) and temperature derivative (W/m2/K)
flux.lwrad = 2 * leaf.emiss * physcon.sigma * flux.tleaf^4;
dlwrad = 8 * leaf.emiss * physcon.sigma * flux.tleaf^3;
% Sensible heat flux (W/m2) and temperature derivative (W/m2/K)
flux.shflx = 2 * atmos.cpair * (flux.tleaf - atmos.tair) * flux.gbh;
dshflx = 2 * atmos.cpair * flux.gbh;
% Latent heat flux (W/m2) and temperature derivative (W/m2/K)
flux.lhflx = lambda_val / atmos.patm * (esat - atmos.eair) * gleaf;
dlhflx = lambda_val / atmos.patm * desat * gleaf;
% Energy balance (W/m2) and temperature derivative (W/m2/K)
f0 = flux.qa - flux.lwrad - flux.shflx - flux.lhflx;
df0 = -dlwrad - dshflx - dlhflx;
% Change in leaf temperature
dtleaf = -f0 / df0;
% Update leaf temperature
flux.tleaf = flux.tleaf + dtleaf;
end
% --- Net radiation
flux.rnet = flux.qa - flux.lwrad;
% --- Error check
err = flux.rnet - flux.shflx - flux.lhflx;
if (abs(err) > f0_max)
fprintf('err = %15.3f\n',err)
fprintf('qa = %15.3f\n',flux.qa)
fprintf('lwrad = %15.3f\n',flux.lwrad)
fprintf('sh = %15.3f\n',flux.shflx)
fprintf('lh = %15.3f\n',flux.lhflx)
error ('LeafTemperature error')
end
% Water vapor flux: W/m2 -> mol H2O/m2/s
flux.etflx = flux.lhflx / lambda_val;
satvap.m | View on GitHub
function [esat, desat] = satvap (tc)
% Compute saturation vapor pressure and change in saturation vapor pressure
% with respect to temperature. Polynomial approximations are from:
% Flatau et al. (1992) Polynomial fits to saturation vapor pressure.
% Journal of Applied Meteorology 31:1507-1513. Input temperature is Celsius.
% --- For water vapor (temperature range is 0C to 100C)
a0 = 6.11213476; b0 = 0.444017302;
a1 = 0.444007856; b1 = 0.286064092e-01;
a2 = 0.143064234e-01; b2 = 0.794683137e-03;
a3 = 0.264461437e-03; b3 = 0.121211669e-04;
a4 = 0.305903558e-05; b4 = 0.103354611e-06;
a5 = 0.196237241e-07; b5 = 0.404125005e-09;
a6 = 0.892344772e-10; b6 = -0.788037859e-12;
a7 = -0.373208410e-12; b7 = -0.114596802e-13;
a8 = 0.209339997e-15; b8 = 0.381294516e-16;
% --- For ice (temperature range is -75C to 0C)
c0 = 6.11123516; d0 = 0.503277922;
c1 = 0.503109514; d1 = 0.377289173e-01;
c2 = 0.188369801e-01; d2 = 0.126801703e-02;
c3 = 0.420547422e-03; d3 = 0.249468427e-04;
c4 = 0.614396778e-05; d4 = 0.313703411e-06;
c5 = 0.602780717e-07; d5 = 0.257180651e-08;
c6 = 0.387940929e-09; d6 = 0.133268878e-10;
c7 = 0.149436277e-11; d7 = 0.394116744e-13;
c8 = 0.262655803e-14; d8 = 0.498070196e-16;
% --- Limit temperature to -75C to 100C
tc = min(tc, 100);
tc = max(tc, -75);
% --- Saturation vapor pressure (esat, mb) and derivative (desat, mb)
if (tc >= 0)
esat = a0 + tc*(a1 + tc*(a2 + tc*(a3 + tc*(a4 ...
+ tc*(a5 + tc*(a6 + tc*(a7 + tc*a8)))))));
desat = b0 + tc*(b1 + tc*(b2 + tc*(b3 + tc*(b4 ...
+ tc*(b5 + tc*(b6 + tc*(b7 + tc*b8)))))));
else
esat = c0 + tc*(c1 + tc*(c2 + tc*(c3 + tc*(c4 ...
+ tc*(c5 + tc*(c6 + tc*(c7 + tc*c8)))))));
desat = d0 + tc*(d1 + tc*(d2 + tc*(d3 + tc*(d4 ...
+ tc*(d5 + tc*(d6 + tc*(d7 + tc*d8)))))));
end
% --- Convert from mb to Pa
esat = esat * 100;
desat = desat * 100;
StomataEfficiency.m | View on GitHub
function [flux, val] = StomataEfficiency (physcon, atmos, leaf, flux, gs_val)
% Stomatal efficiency check to determine maximum gs. For the stomatal conductance
% gs_val, calculate photosynthesis for an increase in stomatal conductance equal
% to "delta". The returned value is positive if this increase produces a change
% in photosynthesis > iota*vpd*delta. The returned value is negative if the increase
% produces a change in photosynthesis < iota*vpd*delta.
% --- Leaf boundary layer conductances
[flux] = LeafBoundaryLayer (physcon, atmos, leaf, flux);
% --- Specify "delta" as a small difference in gs (mol H2O/m2/s)
delta = 0.001;
% --- Calculate photosynthesis at lower gs (gs_val - delta), but first need leaf temperature for this gs
% gs2 - lower value for gs (mol H2O/m2/s)
% an2 - leaf photosynthesis at gs2 (umol CO2/m2/s)
gs2 = gs_val - delta;
flux.gs = gs2;
[flux] = LeafTemperature (physcon, atmos, leaf, flux);
[flux] = LeafPhotosynthesis (physcon, atmos, leaf, flux);
an2 = flux.an;
% --- Calculate photosynthesis at higher gs (gs_val), but first need leaf temperature for this gs
% gs1 - higher value for gs (mol H2O/m2/s)
% an1 - leaf photosynthesis at gs1 (umol CO2/m2/s)
gs1 = gs_val;
flux.gs = gs1;
[flux] = LeafTemperature (physcon, atmos, leaf, flux);
[flux] = LeafPhotosynthesis (physcon, atmos, leaf, flux);
an1 = flux.an;
% --- Efficiency check: val < 0 when d(An) / d(gs) < iota * vpd
val = (an1 - an2) - leaf.iota * delta * (flux.vpd / atmos.patm);
StomataOptimization.m | View on GitHub
function [flux] = StomataOptimization (physcon, atmos, leaf, flux)
% Leaf temperature, energy fluxes, photosynthesis, and stomatal conductance
% with water-use efficiency stomatal optimization
% --- Low and high initial estimates for gs (mol H2O/m2/s)
gs1 = 0.002;
gs2 = 2.0;
% --- Check for minimum stomatal conductance linked to low light
% based on the efficiency check for gs1 and gs2 (check1, check2)
[flux, check1] = StomataEfficiency (physcon, atmos, leaf, flux, gs1);
[flux, check2] = StomataEfficiency (physcon, atmos, leaf, flux, gs2);
if (check1 * check2 < 0)
% Calculate gs using the function StomataEfficiency to iterate gs
% to an accuracy of tol (mol H2O/m2/s)
tol = 0.004;
func_name = 'StomataEfficiency';
[flux, root] = brent_root (func_name, physcon, atmos, leaf, flux, gs1, gs2, tol);
flux.gs = root;
else
% Low light. Set gs to minimum conductance
flux.gs = 0.002;
end
% --- Leaf fluxes for this gs
[flux] = LeafBoundaryLayer (physcon, atmos, leaf, flux);
[flux] = LeafTemperature (physcon, atmos, leaf, flux);
[flux] = LeafPhotosynthesis (physcon, atmos, leaf, flux);
TleafFunc.m | View on GitHub
function [flux, tleaf_dif] = TleafFunc (physcon, atmos, leaf, flux, tleaf_val)
% Calculate leaf temperature and fluxes for an input leaf temperature
% (tleaf_val) and compare the new temperature to the prior
% temperature. This function returns a value tleaf_dif = 0 when leaf
% temperature does not change between iterations.
if (tleaf_val < 0)
error ('TleafFunc error')
end
% --- Current value for leaf temperature
flux.tleaf = tleaf_val;
% --- Leaf boundary layer conductances
[flux] = LeafBoundaryLayer (physcon, atmos, leaf, flux);
% --- Leaf photosynthesis and stomatal conductance
[flux] = LeafPhotosynthesis (physcon, atmos, leaf, flux);
% --- Leaf temperature and energy fluxes
[flux] = LeafTemperature (physcon, atmos, leaf, flux);
% --- Compare with prior value for leaf temperature
tleaf_dif = flux.tleaf - tleaf_val;
Output
Figures
Figure 1
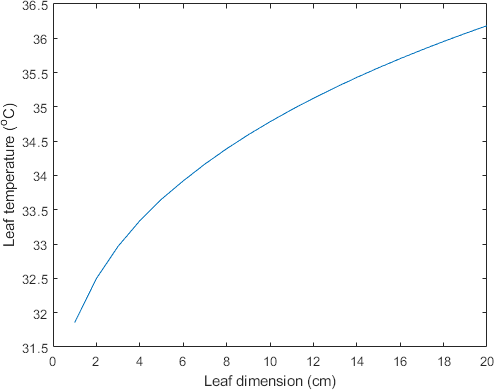
Text
data.txt | View on GitHub | View raw
1.000 1619.200 31.858 1309.288 109.146 2.492 8.311 3.335 2.19512 0.12209
2.000 1619.200 32.498 1309.288 107.742 2.460 7.770 3.158 1.58674 0.11310
3.000 1619.200 32.968 1309.288 104.989 2.397 7.301 3.045 1.31673 0.10514
4.000 1619.200 33.340 1309.288 103.357 2.360 6.974 2.955 1.15432 0.09982
5.000 1619.200 33.655 1309.288 101.859 2.326 6.700 2.880 1.04303 0.09542
6.000 1619.200 33.921 1309.288 101.189 2.311 6.506 2.816 0.96015 0.09247
7.000 1619.200 34.167 1309.288 99.885 2.281 6.297 2.761 0.89592 0.08916
8.000 1619.200 34.390 1309.288 98.659 2.253 6.109 2.712 0.84399 0.08622
9.000 1619.200 34.594 1309.288 97.502 2.226 5.939 2.668 0.80086 0.08356
10.000 1619.200 34.784 1309.288 96.405 2.201 5.784 2.627 0.76429 0.08116
11.000 1619.200 34.960 1309.288 95.363 2.178 5.640 2.590 0.73275 0.07895
12.000 1619.200 35.126 1309.288 94.370 2.155 5.508 2.556 0.70519 0.07692
13.000 1619.200 35.282 1309.288 93.421 2.133 5.384 2.524 0.68082 0.07504
14.000 1619.200 35.430 1309.288 92.514 2.112 5.268 2.494 0.65907 0.07328
15.000 1619.200 35.570 1309.288 91.644 2.093 5.160 2.466 0.63949 0.07165
16.000 1619.200 35.704 1309.288 90.810 2.074 5.058 2.439 0.62175 0.07012
17.000 1619.200 35.832 1309.288 90.009 2.055 4.961 2.414 0.60557 0.06868
18.000 1619.200 35.954 1309.288 89.240 2.038 4.870 2.390 0.59074 0.06732
19.000 1619.200 36.071 1309.288 88.498 2.021 4.783 2.367 0.57707 0.06604
20.000 1619.200 36.184 1309.288 87.783 2.004 4.701 2.345 0.56442 0.06483