Leaf Gas Exchange
Table of contents
Code
Main program
sp_12_01.m | View on GitHub
% Supplemental program 12.1
% -------------------------------------------------------------------------
% Calculate leaf gas exchange for C3 and C4 plants in relation to PAR, CO2,
% temperature, and vapor pressure deficit. For this example, leaf temperature
% is specified (not calculated).
% -------------------------------------------------------------------------
% --- Waveband indices for visible and near-infrared
params.vis = 1; params.nir = 2;
% --- Physical constants
physcon.grav = 9.80665; % Gravitational acceleration (m/s2)
physcon.tfrz = 273.15; % Freezing point of water (K)
physcon.mmh2o = 18.02 / 1000; % Molecular mass of water (kg/mol)
physcon.rgas = 8.31446; % Universal gas constant (J/K/mol)
physcon.visc0 = 13.3e-06; % Kinematic viscosity at 0C and 1013.25 hPa (m2/s)
physcon.Dh0 = 18.9e-06; % Molecular diffusivity (heat) at 0C and 1013.25 hPa (m2/s)
physcon.Dv0 = 21.8e-06; % Molecular diffusivity (H2O) at 0C and 1013.25 hPa (m2/s)
physcon.Dc0 = 13.8e-06; % Molecular diffusivity (CO2) at 0C and 1013.25 hPa (m2/s)
% --- Set leaf physiology variables
% Stomatal conductance: 0 = Medlyn model. 1 = Ball-Berry model. 2 = WUE optimization
leaf.gstyp = 0;
% leaf.gstyp = 1;
% leaf.gstyp = 2;
% Photosynthetic pathway: 1 = C3. 0 = C4
leaf.c3psn = 1;
% leaf.c3psn = 0;
% Photosynthesis co-limitation: 0 = no. 1 = yes
leaf.colim = 1;
% leaf.colim = 0;
% Leaf physiological parameters
[leaf] = LeafPhysiologyParams (params, physcon, leaf);
% --- Plot type: 1 = light. 2 = CO2. 3 = temperature. 4 = vapor pressure deficit
plot_type = 1;
% --- Default conditions
co2conc = 380; % Atmospheric CO2 (umol/mol)
relhum = 80; % Air relative humidity (%)
air_temp = physcon.tfrz + 25; % Air temperature (K)
par_sat = 2000; % Incident PAR (umol photon/m2/s)
leaf_temp = physcon.tfrz + 25; % Leaf temperature (K)
% Atmospheric CO2 (umol/mol) and O2 (mmol/mol)
atmos.co2air = co2conc;
atmos.o2air = 0.209 * 1000;
% Leaf absorbed PAR (umol photon/m2 leaf/s)
atmos.par = par_sat;
flux.apar = atmos.par * (1 - leaf.rho(params.vis) - leaf.tau(params.vis));
% Leaf temperature (K) and saturation vapor pressure (Pa)
flux.tleaf = leaf_temp;
[esat_tleaf, desat_tleaf] = satvap ((flux.tleaf-physcon.tfrz));
% Air temperature (K) and vapor pressure (Pa)
atmos.tair = air_temp;
atmos.relhum = relhum;
[esat_tair, desat_tair] = satvap ((atmos.tair-physcon.tfrz));
atmos.eair = esat_tair * (atmos.relhum / 100);
vpd_tleaf = esat_tleaf - atmos.eair;
% Wind (m/s)
% u = 0.01_r8 ! Still air
% u = 0.1_r8 ! Calm - smoke rises vertically
% u = 1.0_r8 ! Light air - smoke drift indicates wind direction
% u = 2.5_r8 ! Light breeze - wind felt on skin, leaves rustle
% u = 5.0_r8 ! Gentle breeze - leaves constantly moving and light flag extended
% u = 10.0_r8 ! Moderate breeze
atmos.wind = 5;
% Atmospheric pressure (Pa) and molar density (mol/m3)
atmos.patm = 101325;
atmos.rhomol = atmos.patm / (physcon.rgas * atmos.tair);
% --- Leaf boundary layer conductances
[flux] = LeafBoundaryLayer (physcon, atmos, leaf, flux);
% --- Light response at standard CO2, leaf temperature, and VPD
if (plot_type == 1)
p = 0;
for i = 0: 10: 2000
% Set value for PAR
atmos.par = i;
flux.apar = atmos.par * (1 - leaf.rho(params.vis) - leaf.tau(params.vis));
% Calculate photosynthesis and stomatal conductance
if (leaf.gstyp <= 1)
[flux] = LeafPhotosynthesis (physcon, atmos, leaf, flux);
elseif (leaf.gstyp == 2)
[flux] = StomataOptimization (physcon, atmos, leaf, flux);
end
% Save data for output
p = p + 1;
x1(p) = atmos.par;
x2(p) = flux.tleaf - physcon.tfrz;
x3(p) = atmos.co2air;
x4(p) = (esat_tleaf - atmos.eair) * 0.001;
x5(p) = flux.hs;
x6(p) = flux.ci / atmos.co2air;
x7(p) = flux.ac - flux.rd;
x8(p) = flux.aj - flux.rd;
x9(p) = flux.ap - flux.rd;
x10(p) = flux.an;
x11(p) = flux.gs;
x12(p) = flux.gbh;
end
% Plot data
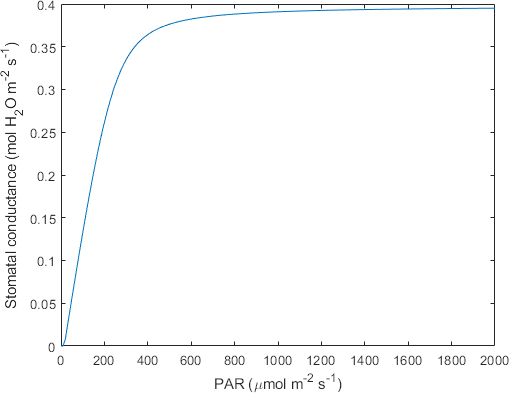
plot(x1,x11)
xlabel('PAR (\mumol m^{-2} s^{-1})')
ylabel('Stomatal conductance (mol H_2O m^{-2} s^{-1})')
% Output data and then clear variables from memory
A = [x1; x2; x3; x4; x5; x6; x7; x8; x9; x10; x11; x12];
filename = 'light_response.txt';
fileID = fopen(filename,'w');
fprintf(fileID,'%6.1f %6.1f %6.1f %9.4f %9.4f %9.4f %9.4f %9.4f %9.4f %9.4f %9.4f %9.4f\n', A);
fclose(fileID);
clear x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 A;
% Reset to default value
atmos.par = par_sat;
flux.apar = atmos.par * (1 - leaf.rho(params.vis) - leaf.tau(params.vis));
end
% --- CO2 response at saturated light and standard leaf temperature and VPD
if (plot_type == 2)
p = 0;
for i = 100: 10: 1000
% Set value for CO2
atmos.co2air = i;
% Calculate photosynthesis and stomatal conductance
if (leaf.gstyp <= 1)
[flux] = LeafPhotosynthesis (physcon, atmos, leaf, flux);
elseif (leaf.gstyp == 2)
[flux] = StomataOptimization (physcon, atmos, leaf, flux);
end
% Save data for output
p = p + 1;
x1(p) = atmos.par;
x2(p) = flux.tleaf - physcon.tfrz;
x3(p) = atmos.co2air;
x4(p) = (esat_tleaf - atmos.eair) * 0.001;
x5(p) = flux.hs;
x6(p) = flux.ci / atmos.co2air;
x7(p) = flux.ac - flux.rd;
x8(p) = flux.aj - flux.rd;
x9(p) = flux.ap - flux.rd;
x10(p) = flux.an;
x11(p) = flux.gs;
x12(p) = flux.gbh;
end
% Plot data
plot(x3,x11)
xlabel('c_a (\mumol mol^{-1})')
ylabel('Stomatal conductance (mol H_2O m^{-2} s^{-1})')
% Output data and then clear variables from memory
A = [x1; x2; x3; x4; x5; x6; x7; x8; x9; x10; x11; x12];
filename = 'co2_response.txt';
fileID = fopen(filename,'w');
fprintf(fileID,'%6.1f %6.1f %6.1f %9.4f %9.4f %9.4f %9.4f %9.4f %9.4f %9.4f %9.4f %9.4f\n', A);
fclose(fileID);
clear x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 A;
% Reset to default value
atmos.co2air = co2conc;
end
% --- Temperature response at saturated light and standard CO2 and constant RH or VPD
if (plot_type == 3)
p = 0;
for i = 10: 1: 35
% Set value for leaf temperature and adjust vapor pressure of air so that
% RH or VPD is constant
flux.tleaf = physcon.tfrz + i;
[esat_current, desat_current] = satvap ((flux.tleaf-physcon.tfrz));
if (leaf.gstyp == 1)
% Adjust vapor pressure of air so that RH is constant
atmos.eair = (relhum / 100) * esat_current;
else
% Adjust vapor pressure of air so that VPD is constant
atmos.eair = esat_current - vpd_tleaf;
end
% Change iota based on temperature
% if (leaf.gstyp == 2)
% ft = @(tl, ha) exp(ha/(physcon.rgas*(physcon.tfrz+25)) * (1-(physcon.tfrz+25)/tl));
% cp_tleaf = leaf.cp25 * ft(flux.tleaf, leaf.cpha);
% leaf.iota = (leaf.iota25 / 1022) * 3 * cp_tleaf / (1.6 * 2.8 * 2.8) * 100;
% end
% Calculate photosynthesis and stomatal conductance
if (leaf.gstyp <= 1)
[flux] = LeafPhotosynthesis (physcon, atmos, leaf, flux);
elseif (leaf.gstyp == 2)
[flux] = StomataOptimization (physcon, atmos, leaf, flux);
end
% Save data for output
p = p + 1;
x1(p) = atmos.par;
x2(p) = flux.tleaf - physcon.tfrz;
x3(p) = atmos.co2air;
x4(p) = (esat_current - atmos.eair) * 0.001;
x5(p) = flux.hs;
x6(p) = flux.ci / atmos.co2air;
x7(p) = flux.ac - flux.rd;
x8(p) = flux.aj - flux.rd;
x9(p) = flux.ap - flux.rd;
x10(p) = flux.an;
x11(p) = flux.gs;
x12(p) = flux.gbh;
end
% Plot data
plot(x2,x11)
xlabel('Temperature (^{o}C)')
ylabel('Stomatal conductance (mol H_2O m^{-2} s^{-1})')
% Output data and then clear variables from memory
A = [x1; x2; x3; x4; x5; x6; x7; x8; x9; x10; x11; x12];
filename = 'temperature_response.txt';
fileID = fopen(filename,'w');
fprintf(fileID,'%6.1f %6.1f %6.1f %9.4f %9.4f %9.4f %9.4f %9.4f %9.4f %9.4f %9.4f %9.4f\n', A);
fclose(fileID);
clear x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 A;
% Reset to default value
flux.tleaf = leaf_temp;
atmos.eair = (relhum / 100) * esat_tleaf;
if (leaf.gstyp == 2)
leaf.iota = leaf.iota25;
end
end
% --- Vapor pressure response at saturated light and standard CO2 and temperature
if (plot_type == 4)
p = 0;
for i = 10: 2: 100
% Set value for vapor pressure of air
[esat, desat] = satvap ((atmos.tair-physcon.tfrz));
atmos.relhum = i;
atmos.eair = esat * (atmos.relhum / 100);
% Calculate photosynthesis and stomatal conductance
if (leaf.gstyp <= 1)
[flux] = LeafPhotosynthesis (physcon, atmos, leaf, flux);
elseif (leaf.gstyp == 2)
[flux] = StomataOptimization (physcon, atmos, leaf, flux);
end
% Save data for output
p = p + 1;
x1(p) = atmos.par;
x2(p) = flux.tleaf - physcon.tfrz;
x3(p) = atmos.co2air;
x4(p) = (esat_tleaf - atmos.eair) * 0.001;
x5(p) = flux.hs;
x6(p) = flux.ci / atmos.co2air;
x7(p) = flux.ac - flux.rd;
x8(p) = flux.aj - flux.rd;
x9(p) = flux.ap - flux.rd;
x10(p) = flux.an;
x11(p) = flux.gs;
x12(p) = flux.gbh;
end
% Plot data
plot(x4,x11)
xlabel('VPD (kPa)')
ylabel('Stomatal conductance (mol H_2O m^{-2} s^{-1})')
% Output data and then clear variables from memory
A = [x1; x2; x3; x4; x5; x6; x7; x8; x9; x10; x11; x12];
filename = 'vpd_response.txt';
fileID = fopen(filename,'w');
fprintf(fileID,'%6.1f %6.1f %6.1f %9.4f %9.4f %9.4f %9.4f %9.4f %9.4f %9.4f %9.4f %9.4f\n', A);
fclose(fileID);
clear x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 A;
% Reset to default value
atmos.relhum = relhum;
[esat, desat] = satvap ((atmos.tair-physcon.tfrz));
atmos.eair = esat * atmos.relhum / 100;
end
Aux. programs
brent_root.m | View on GitHub
function [flux, root] = brent_root (func, physcon, atmos, leaf, flux, xa, xb, tol)
% Use Brent's method to find the root of a function, which is known to exist between
% xa and xb. The root is updated until its accuracy is tol. func is the name of the
% function to solve. The variable root is returned as the root of the function. The
% function being evaluated has the definition statement:
%
% function [flux, fx] = func (physcon, atmos, leaf, flux, x)
%
% The function func is exaluated at x and the returned value is fx. It uses variables
% in the physcon, atmos, leaf, and flux structures. These are passed in as
% input arguments. It also calculates values for variables in the flux structure
% so this must be returned in the function call as an output argument. The matlab
% function feval evaluates func.
% --- Evaluate func at xa and xb and make sure the root is bracketed
a = xa;
b = xb;
[flux, fa] = feval(func, physcon, atmos, leaf, flux, a);
[flux, fb] = feval(func, physcon, atmos, leaf, flux, b);
if ((fa > 0 & fb > 0) | (fa < 0 & fb < 0))
error('brent_root error: root must be bracketed')
end
% --- Initialize iteration
itmax = 50; % Maximum number of iterations
eps1 = 1e-08; % Relative error tolerance
c = b;
fc = fb;
% --- Iterative root calculation
for iter = 1:itmax
if ((fb > 0 & fc > 0) | (fb < 0 & fc < 0))
c = a;
fc = fa;
d = b - a;
e = d;
end
if (abs(fc) < abs(fb))
a = b;
b = c;
c = a;
fa = fb;
fb = fc;
fc = fa;
end
tol1 = 2 * eps1 * abs(b) + 0.5 * tol;
xm = 0.5 * (c - b);
% Check to end iteration
if (abs(xm) <= tol1 | fb == 0)
break
end
if (abs(e) >= tol1 & abs(fa) > abs(fb))
s = fb / fa;
if (a == c)
p = 2 * xm * s;
q = 1 - s;
else
q = fa / fc;
r = fb / fc;
p = s * (2 * xm * q * (q - r) - (b - a) * (r - 1));
q = (q - 1) * (r - 1) * (s - 1);
end
if (p > 0)
q = -q;
end
p = abs(p);
if (2*p < min(3*xm*q-abs(tol1*q), abs(e*q)))
e = d;
d = p / q;
else
d = xm;
e = d;
end
else
d = xm;
e = d;
end
a = b;
fa = fb;
if (abs(d) > tol1)
b = b + d;
else
if (xm >= 0)
b = b + abs(tol1);
else
b = b - abs(tol1);
end
end
[flux, fb] = feval(func, physcon, atmos, leaf, flux, b);
% Check to end iteration
if (fb == 0)
break
end
% Check to see if failed to converge
if (iter == itmax)
error('brent_root error: Maximum number of interations exceeded')
end
end
root = b;
CiFunc.m | View on GitHub
function [flux, ci_dif] = CiFunc (physcon, atmos, leaf, flux, ci_val)
% Calculate leaf photosynthesis and stomatal conductance for a specified Ci
% (ci_val). Then calculate a new Ci from the diffusion equation. This function
% returns a value ci_dif = 0 when Ci has converged to the value that satisfies
% the metabolic, stomatal constraint, and diffusion equations.
% ------------------------------------------------------
% Input
% physcon.tfrz ! Freezing point of water (K)
% atmos.o2air ! Atmospheric O2 (mmol/mol)
% atmos.co2air ! Atmospheric CO2 (umol/mol)
% atmos.eair ! Vapor pressure of air (Pa)
% leaf.c3psn ! Photosynthetic pathway: 1 = C3. 0 = C4 plant
% leaf.gstyp ! Stomatal conductance: 0 = Medlyn. 1 = Ball-Berry. 2 = WUE optimization
% leaf.colim ! Photosynthesis co-limitation: 0 = no. 1 = yes
% leaf.colim_c3 ! Empirical curvature parameter for C3 co-limitation
% leaf.colim_c4a ! Empirical curvature parameter for C4 co-limitation
% leaf.colim_c4b ! Empirical curvature parameter for C4 co-limitation
% leaf.qe_c4 ! C4: Quantum yield (mol CO2 / mol photons)
% leaf.g0 ! Ball-Berry minimum leaf conductance (mol H2O/m2/s)
% leaf.g1 ! Ball-Berry slope of conductance-photosynthesis relationship
% flux.vcmax ! Maximum carboxylation rate (umol/m2/s)
% flux.cp ! CO2 compensation point (umol/mol)
% flux.kc ! Michaelis-Menten constant for CO2 (umol/mol)
% flux.ko ! Michaelis-Menten constant for O2 (mmol/mol)
% flux.je ! Electron transport rate (umol/m2/s)
% flux.kp_c4 ! C4: Initial slope of CO2 response curve (mol/m2/s)
% flux.rd ! Leaf respiration rate (umol CO2/m2 leaf/s)
% flux.gbv ! Leaf boundary layer conductance, H2O (mol H2O/m2 leaf/s)
% flux.gbc ! Leaf boundary layer conductance, CO2 (mol CO2/m2 leaf/s)
% flux.apar ! Leaf absorbed PAR (umol photon/m2 leaf/s)
% flux.tleaf ! Leaf temperature (K)
% ci_val ! Input value for Ci (umol/mol)
%
% Output
% flux.ac ! Leaf Rubisco-limited gross photosynthesis (umol CO2/m2 leaf/s)
% flux.aj ! Leaf RuBP regeneration-limited gross photosynthesis (umol CO2/m2 leaf/s)
% flux.ap ! Leaf product-limited (C3) or CO2-limited (C4) gross photosynthesis (umol CO2/m2 leaf/s)
% flux.ag ! Leaf gross photosynthesis (umol CO2/m2 leaf/s)
% flux.an ! Leaf net photosynthesis (umol CO2/m2 leaf/s)
% flux.cs ! Leaf surface CO2 (umol/mol)
% flux.gs ! Leaf stomatal conductance (mol H2O/m2 leaf/s)
% ci_dif ! Difference in Ci
% ------------------------------------------------------
% --- Metabolic (demand-based) photosynthetic rate
if (leaf.c3psn == 1)
% C3: Rubisco-limited photosynthesis
flux.ac = flux.vcmax * max(ci_val - flux.cp, 0) / (ci_val + flux.kc * (1 + atmos.o2air / flux.ko));
% C3: RuBP regeneration-limited photosynthesis
flux.aj = flux.je * max(ci_val - flux.cp, 0) / (4 * ci_val + 8 * flux.cp);
% C3: Product-limited photosynthesis (do not use)
flux.ap = 0;
else
% C4: Rubisco-limited photosynthesis
flux.ac = flux.vcmax;
% C4: RuBP regeneration-limited photosynthesis
flux.aj = leaf.qe_c4 * flux.apar;
% C4: PEP carboxylase-limited (CO2-limited)
flux.ap = flux.kp_c4 * max(ci_val, 0);
end
% --- Net photosynthesis as the minimum or co-limited rate
if (leaf.colim == 1) % Use co-limitation
% First co-limit Ac and Aj. Ai is the intermediate co-limited photosynthesis
% rate found by solving the polynomial: aquad*Ai^2 + bquad*Ai + cquad = 0 for Ai.
% Correct solution is the smallest of the two roots.
if (leaf.c3psn == 1)
aquad = leaf.colim_c3;
else
aquad = leaf.colim_c4a;
end
bquad = -(flux.ac + flux.aj);
cquad = flux.ac * flux.aj;
pcoeff = [aquad bquad cquad];
proots = roots(pcoeff);
ai = min(proots(1), proots(2));
% Now co-limit again using Ap, but only for C4 plants. Solve the polynomial:
% aquad*Ag^2 + bquad*Ag + cquad = 0 for Ag. Correct solution is the smallest
% of the two roots. Ignore the product-limited rate For C3 plants.
if (leaf.c3psn == 0)
aquad = leaf.colim_c4b;
bquad = -(ai + flux.ap);
cquad = ai * flux.ap;
pcoeff = [aquad bquad cquad];
proots = roots(pcoeff);
flux.ag = min(proots(1), proots(2));
else
flux.ag = ai;
end
elseif (leaf.colim == 0) % No co-limitation
if (leaf.c3psn == 1)
flux.ag = min(flux.ac, flux.aj); % C3
else
flux.ag = min(flux.ac, flux.aj, flux.ap); % C4
end
end
% Prevent photosynthesis from ever being negative
flux.ac = max(flux.ac, 0);
flux.aj = max(flux.aj, 0);
flux.ap = max(flux.ap, 0);
flux.ag = max(flux.ag, 0);
% Net CO2 uptake
flux.an = flux.ag - flux.rd;
% --- CO2 at leaf surface
flux.cs = atmos.co2air - flux.an / flux.gbc;
flux.cs = max(flux.cs, 1);
% --- Stomatal constraint function
% Saturation vapor pressure at leaf temperature
[esat, desat] = satvap ((flux.tleaf-physcon.tfrz));
% Ball-Berry stomatal conductance is a quadratic equation
% for gs given An: aquad*gs^2 + bquad*gs + cquad = 0. Correct
% solution is the larger of the two roots. This solution is
% valid for An >= 0. With An <= 0, gs = g0.
if (leaf.gstyp == 1)
term = flux.an / flux.cs;
if (flux.an > 0)
aquad = 1;
bquad = flux.gbv - leaf.g0 - leaf.g1 * term;
cquad = -flux.gbv * (leaf.g0 + leaf.g1 * term * atmos.eair / esat);
pcoeff = [aquad bquad cquad];
proots = roots(pcoeff);
flux.gs = max(proots(1), proots(2));
else
flux.gs = leaf.g0;
end
end
% Quadratic equation for Medlyn stomatal conductance
if (leaf.gstyp == 0)
vpd = max((esat - atmos.eair), 50) * 0.001;
term = 1.6 * flux.an / flux.cs;
if (flux.an > 0)
aquad = 1;
bquad = -(2 * (leaf.g0 + term) + (leaf.g1 * term)^2 / (flux.gbv * vpd));
cquad = leaf.g0 * leaf.g0 + (2 * leaf.g0 + term * (1 - leaf.g1 * leaf.g1 / vpd)) * term;
pcoeff = [aquad bquad cquad];
proots = roots(pcoeff);
flux.gs = max(proots(1), proots(2));
else
flux.gs = leaf.g0;
end
end
% --- Diffusion (supply-based) photosynthetic rate
% Leaf CO2 conductance (mol CO2/m2/s)
gleaf = 1 / (1 / flux.gbc + 1.6 / flux.gs);
% Calculate Ci from the diffusion rate
cinew = atmos.co2air - flux.an / gleaf;
% --- Return the difference between the current Ci and the new Ci
if (flux.an >= 0)
ci_dif = cinew - ci_val;
else
ci_dif = 0;
end
CiFuncOptimization.m | View on GitHub
function [flux] = CiFuncOptimization (atmos, leaf, flux)
% Calculate leaf photosynthesis for a specified stomatal conductance.
% Then calculate Ci from the diffusion equation.
%
% This routine uses a quadratic equation to solve for net photosynthesis (An).
% A general equation for C3 photosynthesis is:
%
% a*(Ci - Cp)
% An = ----------- - Rd
% e*Ci + d
%
% where:
%
% An = Net leaf photosynthesis (umol CO2/m2/s)
% Rd = Leaf respiration (umol CO2/m2/s)
% Ci = Intercellular CO2 concentration (umol/mol)
% Cp = CO2 compensation point (umol/mol)
%
% Rubisco-limited photosynthesis (Ac)
% a = Vcmax
% e = 1
% d = Kc*(1 + Oi/Ko)
%
% RuBP regeneration-limited photosynthesis (Aj)
% a = J
% e = 4
% d = 8*Cp
%
% where:
%
% Vcmax = Maximum carboxylation rate (umol/m2/s)
% Kc = Michaelis-Menten constant for CO2 (umol/mol)
% Ko = Michaelis-Menten constant for O2 (mmol/mol)
% Oi = Intercellular O2 concentration (mmol/mol)
% J = Electron transport rate (umol/m2/s)
%
% Ci is calculated from the diffusion equation:
%
% 1.4 1.6
% An = (Ca - Ci) / (--- + ---)
% gb gs
%
% 1.4 1.6
% Ci = Ca - (--- + ---)*An
% gb gs
%
% where:
%
% Ca = Atmospheric CO2 concentration (umol/mol)
% gb = Leaf boundary layer conductance (mol H2O/m2/s)
% gs = Leaf stomatal conductance (mol H2O/m2/s)
% 1.4 = Corrects gb for the diffusivity of CO2 compared with H2O
% 1.6 = Corrects gs for the diffusivity of CO2 compared with H2O
%
% The resulting quadratic equation is: a*An^2 + b*An + c = 0, which
% is solved for An. Correct solution is the smaller of the two roots.
%
% A similar approach is used for C4 photosynthesis.
% ------------------------------------------------------
% Input
% atmos.o2air ! Atmospheric O2 (mmol/mol)
% atmos.co2air ! Atmospheric CO2 (umol/mol)
% leaf.c3psn ! Photosynthetic pathway: 1 = C3. 0 = C4 plant
% leaf.colim ! Photosynthesis co-limitation: 0 = no. 1 = yes
% leaf.colim_c3 ! Empirical curvature parameter for C3 co-limitation
% leaf.colim_c4a ! Empirical curvature parameter for C4 co-limitation
% leaf.colim_c4b ! Empirical curvature parameter for C4 co-limitation
% leaf.qe_c4 ! C4: Quantum yield (mol CO2 / mol photons)
% flux.vcmax ! Maximum carboxylation rate (umol/m2/s)
% flux.cp ! CO2 compensation point (umol/mol)
% flux.kc ! Michaelis-Menten constant for CO2 (umol/mol)
% flux.ko ! Michaelis-Menten constant for O2 (mmol/mol)
% flux.je ! Electron transport rate (umol/m2/s)
% flux.kp_c4 ! C4: Initial slope of CO2 response curve (mol/m2/s)
% flux.gs ! Leaf stomatal conductance (mol H2O/m2 leaf/s)
% flux.gbc ! Leaf boundary layer conductance, CO2 (mol CO2/m2 leaf/s)
% flux.apar ! Leaf absorbed PAR (umol photon/m2 leaf/s)
% flux.rd ! Leaf respiration rate (umol CO2/m2 leaf/s)
%
% Output
% flux.ac ! Leaf Rubisco-limited gross photosynthesis (umol CO2/m2 leaf/s)
% flux.aj ! Leaf RuBP regeneration-limited gross photosynthesis (umol CO2/m2 leaf/s)
% flux.ap ! Leaf product-limited (C3) or CO2-limited (C4) gross photosynthesis (umol CO2/m2 leaf/s)
% flux.ag ! Leaf gross photosynthesis (umol CO2/m2 leaf/s)
% flux.an ! Leaf net photosynthesis (umol CO2/m2 leaf/s)
% flux.cs ! Leaf surface CO2 (umol/mol)
% flux.ci ! Leaf intercellular CO2 (umol/mol)
% ------------------------------------------------------
% --- Leaf conductance
% gbc has units mol CO2/m2/s
% gs has units mol H2O/m2/s
% gleaf has units mol CO2/m2/s
gleaf = 1 / (1 / flux.gbc + 1.6 / flux.gs);
% --- Gross assimilation rates
if (leaf.c3psn == 1)
% C3: Rubisco-limited photosynthesis
a0 = flux.vcmax;
e0 = 1;
d0 = flux.kc * (1 + atmos.o2air / flux.ko);
aquad = e0 / gleaf;
bquad = -(e0 * atmos.co2air + d0) - (a0 - e0 * flux.rd) / gleaf;
cquad = a0 * (atmos.co2air - flux.cp) - flux.rd * (e0 * atmos.co2air + d0);
pcoeff = [aquad bquad cquad];
proots = roots(pcoeff);
flux.ac = min(proots(1), proots(2)) + flux.rd;
% C3: RuBP regeneration-limited photosynthesis
a0 = flux.je;
e0 = 4;
d0 = 8 * flux.cp;
aquad = e0 / gleaf;
bquad = -(e0 * atmos.co2air + d0) - (a0 - e0 * flux.rd) / gleaf;
cquad = a0 * (atmos.co2air - flux.cp) - flux.rd * (e0 * atmos.co2air + d0);
pcoeff = [aquad bquad cquad];
proots = roots(pcoeff);
flux.aj = min(proots(1), proots(2)) + flux.rd;
% C3: Product-limited photosynthesis
flux.ap = 0;
else
% C4: Rubisco-limited photosynthesis
flux.ac = flux.vcmax;
% C4: RuBP-limited photosynthesis
flux.aj = leaf.qe_c4 * flux.apar;
% C4: PEP carboxylase-limited (CO2-limited)
flux.ap = flux.kp_c4 * (atmos.co2air * gleaf + flux.rd) / (gleaf + flux.kp_c4);
end
% --- Net assimilation as the minimum or co-limited rate
if (leaf.colim == 1) % Use co-limitation
% First co-limit Ac and Aj. Ai is the intermediate co-limited photosynthesis
% rate found by solving the polynomial: aquad*Ai^2 + bquad*Ai + cquad = 0 for Ai.
% Correct solution is the smallest of the two roots.
if (leaf.c3psn == 1)
aquad = leaf.colim_c3;
else
aquad = leaf.colim_c4a;
end
bquad = -(flux.ac + flux.aj);
cquad = flux.ac * flux.aj;
pcoeff = [aquad bquad cquad];
proots = roots(pcoeff);
ai = min(proots(1), proots(2));
% Now co-limit again using Ap, but only for C4 plants. Solve the polynomial:
% aquad*Ag^2 + bquad*Ag + cquad = 0 for Ag. Correct solution is the smallest
% of the two roots. Ignore the product-limited rate For C3 plants.
if (leaf.c3psn == 0)
aquad = leaf.colim_c4b;
bquad = -(ai + flux.ap);
cquad = ai * flux.ap;
pcoeff = [aquad bquad cquad];
proots = roots(pcoeff);
flux.ag = min(proots(1), proots(2));
else
flux.ag = ai;
end
elseif (leaf.colim == 0) % No co-limitation
if (leaf.c3psn == 1)
flux.ag = min(flux.ac, flux.aj); % C3
else
flux.ag = min(flux.ac, flux.aj, flux.ap); % C4
end
end
% Prevent photosynthesis from ever being negative
flux.ac = max(flux.ac, 0);
flux.aj = max(flux.aj, 0);
flux.ap = max(flux.ap, 0);
flux.ag = max(flux.ag, 0);
% Net CO2 uptake
flux.an = flux.ag - flux.rd;
% --- CO2 at leaf surface
flux.cs = atmos.co2air - flux.an / flux.gbc;
flux.cs = max(flux.cs, 1);
% --- Intercelluar CO2
flux.ci = atmos.co2air - flux.an / gleaf;
hybrid_root.m | View on GitHub
function [flux, root] = hybrid_root (func, physcon, atmos, leaf, flux, xa, xb, tol)
% Solve for the root of a function using the secant and Brent's methods given
% initial estimates xa and xb. The root is updated until its accuracy is tol.
% func is the name of the function to solve. The variable root is returned as
% the root of the function. The function being evaluated has the definition statement:
%
% function [flux, fx] = func (physcon, atmos, leaf, flux, x)
%
% The function func is exaluated at x and the returned value is fx. It uses variables
% in the physcon, atmos, leaf, and flux structures. These are passed in as
% input arguments. It also calculates values for variables in the flux structure
% so this must be returned in the function call as an output argument. The matlab
% function feval evaluates func.
% --- Evaluate func at xa and see if this is the root
x0 = xa;
[flux, f0] = feval(func, physcon, atmos, leaf, flux, x0);
if (f0 == 0)
root = x0;
return
end
% --- Evaluate func at xb and see if this is the root
x1 = xb;
[flux, f1] = feval(func, physcon, atmos, leaf, flux, x1);
if (f1 == 0)
root = x1;
return
end
% --- Order initial root estimates correctly
if (f1 < f0)
minx = x1;
minf = f1;
else
minx = x0;
minf = f0;
end
% --- Iterative root calculation. Use the secant method, with Brent's method as a backup
itmax = 40;
for iter = 1:itmax
dx = -f1 * (x1 - x0) / (f1 - f0);
x = x1 + dx;
% Check if x is the root. If so, exit the iteration
if (abs(dx) < tol)
x0 = x;
break
end
% Evaluate the function at x
x0 = x1;
f0 = f1;
x1 = x;
[flux, f1] = feval(func, physcon, atmos, leaf, flux, x1);
if (f1 < minf)
minx = x1;
minf = f1;
end
% If a root zone is found, use Brent's method for a robust backup strategy
% and exit the iteration
if (f1 * f0 < 0)
[flux, x] = brent_root (func, physcon, atmos, leaf, flux, x0, x1, tol);
x0 = x;
break
end
% In case of failing to converge within itmax iterations stop at the minimum function
if (iter == itmax)
[flux, f1] = feval(func, physcon, atmos, leaf, flux, minx);
x0 = minx;
end
end
root = x0;
latvap.m | View on GitHub
function [val] = latvap (tc, mmh2o)
% Latent heat of vaporization (J/mol) at temperature tc (degC)
val = 2501.6 - 2.3773 * tc; % Latent heat of vaporization (J/g)
val = val * 1000; % Convert from J/g to J/kg
val = val * mmh2o; % Convert from J/kg to J/mol
LeafBoundaryLayer.m | View on GitHub
function [flux] = LeafBoundaryLayer (physcon, atmos, leaf, flux)
% Leaf boundary layer conductances
% -------------------------------------------------------------------------
% Input
% physcon.grav ! Gravitational acceleration (m/s2)
% physcon.tfrz ! Freezing point of water (K)
% physcon.visc0 ! Kinematic viscosity at 0C and 1013.25 hPa (m2/s)
% physcon.Dh0 ! Molecular diffusivity (heat) at 0C and 1013.25 hPa (m2/s)
% physcon.Dv0 ! Molecular diffusivity (H2O) at 0C and 1013.25 hPa (m2/s)
% physcon.Dc0 ! Molecular diffusivity (CO2) at 0C and 1013.25 hPa (m2/s)
% atmos.patm ! Atmospheric pressure (Pa)
% atmos.rhomol ! Molar density mol/m3)
% atmos.wind ! Wind speed (m/s)
% atmos.tair ! Air temperature (K)
% leaf.dleaf ! Leaf dimension (m)
% flux.tleaf ! Leaf temperature (K)
%
% Output
% flux.gbh ! Leaf boundary layer conductance, heat (mol/m2 leaf/s)
% flux.gbv ! Leaf boundary layer conductance, H2O (mol H2O/m2 leaf/s)
% flux.gbc ! Leaf boundary layer conductance, CO2 (mol CO2/m2 leaf/s)
% -------------------------------------------------------------------------
% --- Adjust diffusivity for temperature and pressure
fac = 101325 / atmos.patm * (atmos.tair / physcon.tfrz)^1.81;
visc = physcon.visc0 * fac; % Kinematic viscosity (m2/s)
Dh = physcon.Dh0 * fac; % Molecular diffusivity, heat (m2/s)
Dv = physcon.Dv0 * fac; % Molecular diffusivity, H2O (m2/s)
Dc = physcon.Dc0 * fac; % Molecular diffusivity, CO2 (m2/s)
% --- Dimensionless numbers
Re = atmos.wind * leaf.dleaf / visc; % Reynolds number
Pr = visc / Dh; % Prandtl number
Scv = visc / Dv; % Schmidt number for H2O
Scc = visc / Dc; % Schmidt number for CO2
% Grashof number
Gr = physcon.grav * leaf.dleaf^3 * max(flux.tleaf-atmos.tair, 0) / (atmos.tair * visc * visc);
% --- Empirical correction factor for Nu and Sh
b1 = 1.5;
% --- Nusselt number (Nu) and Sherwood numbers (H2O: Shv, CO2: Shc)
% Forced convection - laminar flow
Nu_lam = b1 * 0.66 * Pr^0.33 * Re^0.5; % Nusselt number
Shv_lam = b1 * 0.66 * Scv^0.33 * Re^0.5; % Sherwood number, H2O
Shc_lam = b1 * 0.66 * Scc^0.33 * Re^0.5; % Sherwood number, CO2
% Forced convection - turbulent flow
Nu_turb = b1 * 0.036 * Pr^0.33 * Re^0.8; % Nusselt number
Shv_turb = b1 * 0.036 * Scv^0.33 * Re^0.8; % Sherwood number, H2O
Shc_turb = b1 * 0.036 * Scc^0.33 * Re^0.8; % Sherwood number, CO2
% Choose correct flow regime for forced convection
Nu_forced = max(Nu_lam, Nu_turb);
Shv_forced = max(Shv_lam, Shv_turb);
Shc_forced = max(Shc_lam, Shc_turb);
% Free convection
Nu_free = 0.54 * Pr^0.25 * Gr^0.25; % Nusselt number
Shv_free = 0.54 * Scv^0.25 * Gr^0.25; % Sherwood number, H2O
Shc_free = 0.54 * Scc^0.25 * Gr^0.25; % Sherwood number, CO2
% Both forced and free convection regimes occur together
Nu = Nu_forced + Nu_free;
Shv = Shv_forced + Shv_free;
Shc = Shc_forced + Shc_free;
% --- Boundary layer conductances (m/s)
flux.gbh = Dh * Nu / leaf.dleaf;
flux.gbv = Dv * Shv / leaf.dleaf;
flux.gbc = Dc * Shc / leaf.dleaf;
% --- Convert conductance (m/s) to (mol/m2/s)
flux.gbh = flux.gbh * atmos.rhomol;
flux.gbv = flux.gbv * atmos.rhomol;
flux.gbc = flux.gbc * atmos.rhomol;
LeafPhotosynthesis.m | View on GitHub
function [flux] = LeafPhotosynthesis (physcon, atmos, leaf, flux)
% Calculate leaf photosynthesis using one of two methods:
% (1) Calculate leaf photosynthesis and stomatal conductance
% by solving for the value of Ci that satisfies the
% metabolic, stomatal constraint, and diffusion equations.
% This is used with the Ball-Berry style stomatal models.
% (2) Calculate leaf photosynthesis for a specified stomatal
% conductance. Then calculate Ci from the diffusion equation.
% This is used with the WUE stomatal optimization.
% ------------------------------------------------------
% Input
% physcon.tfrz ! Freezing point of water (K)
% physcon.rgas ! Universal gas constant (J/K/mol)
% atmos.co2air ! Atmospheric CO2 (umol/mol)
% atmos.eair ! Vapor pressure of air (Pa)
% leaf.gstyp ! Stomatal conductance: 0 = Medlyn. 1 = Ball-Berry. 2 = WUE optimization
% leaf.c3psn ! Photosynthetic pathway: 1 = C3. 0 = C4 plant
% leaf.vcmax25 ! Maximum carboxylation rate at 25C (umol/m2/s)
% leaf.jmax25 ! Maximum electron transport rate at 25C (umol/m2/s)
% leaf.rd25 ! Leaf respiration rate at 25C (umol CO2/m2/s)
% leaf.kc25 ! Michaelis-Menten constant for CO2 at 25C (umol/mol)
% leaf.ko25 ! Michaelis-Menten constant for O2 at 25C (mmol/mol)
% leaf.cp25 ! CO2 compensation point at 25C (umol/mol)
% leaf.kcha ! Activation energy for Kc (J/mol)
% leaf.koha ! Activation energy for Ko (J/mol)
% leaf.cpha ! Activation energy for Cp (J/mol)
% leaf.vcmaxha ! Activation energy for Vcmax (J/mol)
% leaf.jmaxha ! Activation energy for Jmax (J/mol)
% leaf.rdha ! Activation energy for Rd (J/mol)
% leaf.vcmaxhd ! Deactivation energy for Vcmax (J/mol)
% leaf.jmaxhd ! Deactivation energy for Jmax (J/mol)
% leaf.rdhd ! Deactivation energy for Rd (J/mol)
% leaf.vcmaxse ! Entropy term for Vcmax (J/mol/K)
% leaf.jmaxse ! Entropy term for Jmax (J/mol/K)
% leaf.rdse ! Entropy term for Rd (J/mol/K)
% leaf.vcmaxc ! Vcmax scaling factor for high temperature inhibition (25 C = 1.0)
% leaf.jmaxc ! Jmax scaling factor for high temperature inhibition (25 C = 1.0)
% leaf.rdc ! Rd scaling factor for high temperature inhibition (25 C = 1.0)
% leaf.phi_psii ! Quantum yield of PS II
% leaf.theta_j ! Empirical curvature parameter for electron transport rate
% leaf.kp25_c4 ! C4: Initial slope of CO2 response curve at 25C (mol/m2/s)
% leaf.g0 ! Ball-Berry minimum leaf conductance (mol H2O/m2/s)
% leaf.g1 ! Ball-Berry slope of conductance-photosynthesis relationship
% flux.gbv ! Leaf boundary layer conductance, H2O (mol H2O/m2 leaf/s)
% flux.gbc ! Leaf boundary layer conductance, CO2 (mol CO2/m2 leaf/s)
% flux.apar ! Leaf absorbed PAR (umol photon/m2 leaf/s)
% flux.tleaf ! Leaf temperature (K)
%
% Input or output (depending on method)
% flux.gs ! Leaf stomatal conductance (mol H2O/m2 leaf/s)
%
% Output
% flux.vcmax ! Maximum carboxylation rate (umol/m2/s)
% flux.jmax ! Maximum electron transport rate (umol/m2/s)
% flux.cp ! CO2 compensation point (umol/mol)
% flux.kc ! Michaelis-Menten constant for CO2 (umol/mol)
% flux.ko ! Michaelis-Menten constant for O2 (mmol/mol)
% flux.je ! Electron transport rate (umol/m2/s)
% flux.kp_c4 ! C4: Initial slope of CO2 response curve (mol/m2/s)
% flux.ac ! Leaf Rubisco-limited gross photosynthesis (umol CO2/m2 leaf/s)
% flux.aj ! Leaf RuBP regeneration-limited gross photosynthesis (umol CO2/m2 leaf/s)
% flux.ap ! Leaf product-limited (C3) or CO2-limited (C4) gross photosynthesis (umol CO2/m2 leaf/s)
% flux.ag ! Leaf gross photosynthesis (umol CO2/m2 leaf/s)
% flux.an ! Leaf net photosynthesis (umol CO2/m2 leaf/s)
% flux.rd ! Leaf respiration rate (umol CO2/m2 leaf/s)
% flux.cs ! Leaf surface CO2 (umol/mol)
% flux.ci ! Leaf intercellular CO2 (umol/mol)
% flux.hs ! Leaf fractional humidity at surface (dimensionless)
% flux.vpd ! Leaf vapor pressure deficit at surface (Pa)
% ------------------------------------------------------
% --- Adjust photosynthetic parameters for temperature
if (leaf.c3psn == 1)
% C3 temperature response
ft = @(tl, ha) exp(ha/(physcon.rgas*(physcon.tfrz+25)) * (1-(physcon.tfrz+25)/tl));
fth = @(tl, hd, se, fc) fc / (1 + exp((-hd+se*tl)/(physcon.rgas*tl)));
flux.kc = leaf.kc25 * ft(flux.tleaf, leaf.kcha);
flux.ko = leaf.ko25 * ft(flux.tleaf, leaf.koha);
flux.cp = leaf.cp25 * ft(flux.tleaf, leaf.cpha);
t1 = ft(flux.tleaf, leaf.vcmaxha);
t2 = fth(flux.tleaf, leaf.vcmaxhd, leaf.vcmaxse, leaf.vcmaxc);
flux.vcmax = leaf.vcmax25 * t1 * t2;
t1 = ft(flux.tleaf, leaf.jmaxha);
t2 = fth(flux.tleaf, leaf.jmaxhd, leaf.jmaxse, leaf.jmaxc);
flux.jmax = leaf.jmax25 * t1 * t2;
t1 = ft(flux.tleaf, leaf.rdha);
t2 = fth(flux.tleaf, leaf.rdhd, leaf.rdse, leaf.rdc);
flux.rd = leaf.rd25 * t1 * t2;
flux.kp_c4 = 0;
elseif (leaf.c3psn == 0)
% C4 temperature response
t1 = 2^((flux.tleaf-(physcon.tfrz+25)) / 10);
t2 = 1 + exp(0.2*((physcon.tfrz+15)-flux.tleaf));
t3 = 1 + exp(0.3*(flux.tleaf-(physcon.tfrz+40)));
flux.vcmax = leaf.vcmax25 * t1 / (t2 * t3);
t3 = 1 + exp(1.3*(flux.tleaf-(physcon.tfrz+55)));
flux.rd = leaf.rd25 * t1 / t3;
flux.kp_c4 = leaf.kp25_c4 * t1;
flux.kc = 0;
flux.ko = 0;
flux.cp = 0;
flux.jmax = 0;
flux.je = 0;
end
% --- Electron transport rate for C3 plants
% Solve the polynomial: aquad*Je^2 + bquad*Je + cquad = 0
% for Je. Correct solution is the smallest of the two roots.
if (leaf.c3psn == 1)
qabs = 0.5 * leaf.phi_psii * flux.apar;
aquad = leaf.theta_j;
bquad = -(qabs + flux.jmax);
cquad = qabs * flux.jmax;
pcoeff = [aquad bquad cquad];
proots = roots(pcoeff);
flux.je = min(proots(1), proots(2));
end
% --- Ci calculation
if (leaf.gstyp <= 1)
% Initial estimates for Ci
if (leaf.c3psn == 1)
ci0 = 0.7 * atmos.co2air;
elseif (leaf.c3psn == 0)
ci0 = 0.4 * atmos.co2air;
end
ci1 = ci0 * 0.99;
% Solve for Ci: Use CiFunc to iterate photosynthesis calculations
% until the change in Ci is < tol. Ci has units umol/mol
tol = 0.1; % Accuracy tolerance for Ci (umol/mol)
func_name = 'CiFunc'; % The function name
[flux, dummy] = hybrid_root (func_name, physcon, atmos, leaf, flux, ci0, ci1, tol);
flux.ci = dummy;
elseif (leaf.gstyp == 2)
% Calculate photosynthesis for a specified stomatal conductance
[flux] = CiFuncOptimization (atmos, leaf, flux);
end
% --- Relative humidity and vapor pressure at leaf surface
[esat, desat] = satvap ((flux.tleaf-physcon.tfrz));
flux.hs = (flux.gbv * atmos.eair + flux.gs * esat) / ((flux.gbv + flux.gs) * esat);
flux.vpd = max(esat - flux.hs*esat, 0.1);
% --- Make sure iterative solution is correct
if (flux.gs < 0)
error ('LeafPhotosynthesis: negative stomatal conductance')
end
% Compare with Ball-Berry model. The solution blows up with low eair. In input
% data, eair should be > 0.05*esat to ensure that hs does not go to zero.
if (leaf.gstyp == 1)
gs_err = leaf.g1 * max(flux.an, 0) * flux.hs / flux.cs + leaf.g0;
if (abs(flux.gs-gs_err)*1e06 > 1e-04)
fprintf('gs = %15.4f\n', flux.gs)
fprintf('gs_err = %15.4f\n', gs_err)
error ('LeafPhotosynthesis: failed Ball-Berry error check')
end
end
% Compare with Medlyn model. The solutions blows up with vpd = 0. The
% quadratic calcuation of gsw in CiFunc constrains vpd > 50 Pa, so this
% comparison is only valid for those conditions.
if (leaf.gstyp == 0)
if ((esat - atmos.eair) > 50)
gs_err = 1.6 * (1 + leaf.g1 / sqrt(flux.vpd*0.001)) * max(flux.an, 0) / flux.cs + leaf.g0;
if (abs(flux.gs-gs_err)*1e06 > 1e-04)
fprintf('gs = %15.4f\n', flux.gs)
fprintf('gs_err = %15.4f\n', gs_err)
error ('LeafPhotosynthesis: failed Medlyn error check')
end
end
end
% Compare with diffusion equation: An = (ca - ci) * gleaf
an_err = (atmos.co2air - flux.ci) / (1 / flux.gbc + 1.6 / flux.gs);
if (flux.an > 0 & abs(flux.an-an_err) > 0.01)
fprintf('An = %15.4f\n', flux.an)
fprintf('An_err = %15.4f\n', an_err)
error ('LeafPhotosynthesis: failed diffusion error check')
end
LeafPhysiologyParams.m | View on GitHub
function [leaf] = LeafPhysiologyParams (params, physcon, leaf)
% ------------------------------------------------------
% Input
% params.vis ! Waveband index for visible radiation
% physcon.tfrz ! Freezing point of water (K)
% physcon.rgas ! Universal gas constant (J/K/mol)
% leaf.c3psn ! Photosynthetic pathway: 1 = C3. 0 = C4 plant
% leaf.gstyp ! Stomatal conductance: 0 = Medlyn. 1 = Ball-Berry. 2 = WUE optimization
%
% Output
% leaf.vcmax25 ! Maximum carboxylation rate at 25C (umol/m2/s)
% leaf.jmax25 ! Maximum electron transport rate at 25C (umol/m2/s)
% leaf.rd25 ! Leaf respiration rate at 25C (umol CO2/m2/s)
% leaf.kc25 ! Michaelis-Menten constant for CO2 at 25C (umol/mol)
% leaf.ko25 ! Michaelis-Menten constant for O2 at 25C (mmol/mol)
% leaf.cp25 ! CO2 compensation point at 25C (umol/mol)
% leaf.kcha ! Activation energy for Kc (J/mol)
% leaf.koha ! Activation energy for Ko (J/mol)
% leaf.cpha ! Activation energy for Cp (J/mol)
% leaf.vcmaxha ! Activation energy for Vcmax (J/mol)
% leaf.jmaxha ! Activation energy for Jmax (J/mol)
% leaf.rdha ! Activation energy for Rd (J/mol)
% leaf.vcmaxhd ! Deactivation energy for Vcmax (J/mol)
% leaf.jmaxhd ! Deactivation energy for Jmax (J/mol)
% leaf.rdhd ! Deactivation energy for Rd (J/mol)
% leaf.vcmaxse ! Entropy term for Vcmax (J/mol/K)
% leaf.jmaxse ! Entropy term for Jmax (J/mol/K)
% leaf.rdse ! Entropy term for Rd (J/mol/K)
% leaf.vcmaxc ! Vcmax scaling factor for high temperature inhibition (25 C = 1.0)
% leaf.jmaxc ! Jmax scaling factor for high temperature inhibition (25 C = 1.0)
% leaf.rdc ! Rd scaling factor for high temperature inhibition (25 C = 1.0)
% leaf.phi_psii ! Quantum yield of PS II
% leaf.theta_j ! Empirical curvature parameter for electron transport rate
% leaf.colim_c3 ! Empirical curvature parameter for C3 co-limitation
% leaf.colim_c4a ! Empirical curvature parameter for C4 co-limitation
% leaf.colim_c4b ! Empirical curvature parameter for C4 co-limitation
% leaf.qe_c4 ! C4: Quantum yield (mol CO2 / mol photons)
% leaf.kp25_c4 ! C4: Initial slope of CO2 response curve at 25C (mol/m2/s)
% leaf.g0 ! Minimum leaf conductance (mol H2O/m2/s)
% leaf.g1 ! Slope of conductance-photosynthesis relationship
% leaf.dleaf ! Leaf dimension (m)
% leaf.rho ! Leaf reflectance for visible (vis) and near-infrared (nir) wavebands
% leaf.tau ! Leaf transmittance for visible (vis) and near-infrared (nir) wavebands
% leaf.iota ! Stomatal efficiency (umol CO2/ mol H2O)
% leaf.iota25 ! Stomatal efficiency at 25C (umol CO2/ mol H2O)
% ------------------------------------------------------
% --- Vcmax and other parameters (at 25C)
if (leaf.c3psn == 1)
leaf.vcmax25 = 57.7;
leaf.jmax25 = 1.67 * leaf.vcmax25;
leaf.kp25_c4 = 0;
leaf.rd25 = 0.015 * leaf.vcmax25;
else
leaf.vcmax25 = 40;
leaf.jmax25 = 0;
leaf.kp25_c4 = 0.02 * leaf.vcmax25;
leaf.rd25 = 0.025 * leaf.vcmax25;
end
% --- Kc, Ko, Cp at 25C
leaf.kc25 = 404.9;
leaf.ko25 = 278.4;
leaf.cp25 = 42.75;
% --- Activation energy
leaf.kcha = 79430;
leaf.koha = 36380;
leaf.cpha = 37830;
leaf.rdha = 46390;
leaf.vcmaxha = 65330;
leaf.jmaxha = 43540;
% --- High temperature deactivation
% Deactivation energy (J/mol)
leaf.rdhd = 150000;
leaf.vcmaxhd = 150000;
leaf.jmaxhd = 150000;
% Entropy term (J/mol/K)
leaf.rdse = 490;
leaf.vcmaxse = 490;
leaf.jmaxse = 490;
% Scaling factors for high temperature inhibition (25 C = 1.0).
% The factor "c" scales the deactivation to a value of 1.0 at 25C.
fth25 = @(hd, se) 1 + exp((-hd + se*(physcon.tfrz+25)) / (physcon.rgas*(physcon.tfrz+25)));
leaf.vcmaxc = fth25 (leaf.vcmaxhd, leaf.vcmaxse);
leaf.jmaxc = fth25 (leaf.jmaxhd, leaf.jmaxse);
leaf.rdc = fth25 (leaf.rdhd, leaf.rdse);
% --- C3 parameters
% Quantum yield of PS II
leaf.phi_psii = 0.85;
% Empirical curvature parameter for electron transport rate
leaf.theta_j = 0.90;
% Empirical curvature parameter for C3 co-limitation
leaf.colim_c3 = 0.98;
% Empirical curvature parameters for C4 co-limitation
leaf.colim_c4a = 0.80;
leaf.colim_c4b = 0.95;
% --- C4: Quantum yield (mol CO2 / mol photons)
leaf.qe_c4 = 0.05;
% --- Stomatal conductance parameters
if (leaf.c3psn == 1)
if (leaf.gstyp == 1)
leaf.g0 = 0.01; % Ball-Berry minimum leaf conductance (mol H2O/m2/s)
leaf.g1 = 9.0; % Ball-Berry slope of conductance-photosynthesis relationship
elseif (leaf.gstyp == 0)
leaf.g0 = 0.0; % Medlyn minimum leaf conductance (mol H2O/m2/s)
leaf.g1 = 4.45; % Medlyn slope of conductance-photosynthesis relationship
% leaf.g1 = 2.8; % To match Ball-Berry g1 = 9
end
else
if (leaf.gstyp == 1)
leaf.g0 = 0.04; % Ball-Berry minimum leaf conductance (mol H2O/m2/s)
leaf.g1 = 4.0; % Ball-Berry slope of conductance-photosynthesis relationship
elseif (leaf.gstyp == 0)
leaf.g0 = 0.0; % Medlyn minimum leaf conductance (mol H2O/m2/s)
leaf.g1 = 1.62; % Medlyn slope of conductance-photosynthesis relationship
end
end
% --- Stomatal efficiency for optimization (An/E; umol CO2/ mol H2O)
if (leaf.gstyp == 2)
leaf.iota25 = 750;
% leaf.iota25 = 1400; % To match Ball-Berry g1 = 9
leaf.iota = leaf.iota25;
end
% --- Leaf dimension (m)
leaf.dleaf = 0.05;
% --- Leaf reflectance and transmittance: visible and near-infrared wavebands
leaf.rho(params.vis) = 0.10;
leaf.tau(params.vis) = 0.10;
LeafTranspiration.m | View on GitHub
function [flux] = LeafTranspiration (physcon, atmos, flux)
% Leaf transpiration flux
% ------------------------------------------------------
% Input
% physcon.tfrz ! Freezing point of water (K)
% physcon.mmh2o ! Molecular mass of water (kg/mol)
% atmos.patm ! Atmospheric pressure (Pa)
% atmos.tair ! Air temperature (K)
% atmos.eair ! Vapor pressure of air (Pa)
% flux.gbv ! Leaf boundary layer conductance, H2O (mol H2O/m2 leaf/s)
% flux.gs ! Leaf stomatal conductance (mol H2O/m2 leaf/s)
% flux.tleaf ! Leaf temperature (K)
%
% Output
% flux.lhflx ! Leaf latent heat flux (W/m2 leaf)
% flux.etflx ! Leaf transpiration flux (mol H2O/m2 leaf/s)
% ------------------------------------------------------
% Latent heat of vaporization (J/mol)
[lambda_val] = latvap ((atmos.tair-physcon.tfrz), physcon.mmh2o);
% Saturation vapor pressure (Pa) and temperature derivative (Pa/K)
[esat, desat] = satvap ((flux.tleaf-physcon.tfrz));
% Leaf conductance for water vapor (mol H2O/m2/s)
gleaf = flux.gs * flux.gbv / (flux.gs + flux.gbv);
% Latent heat flux (W/m2)
flux.lhflx = lambda_val / atmos.patm * (esat - atmos.eair) * gleaf;
% Water vapor flux: W/m2 -> mol H2O/m2/s
flux.etflx = flux.lhflx / lambda_val;
satvap.m | View on GitHub
function [esat, desat] = satvap (tc)
% Compute saturation vapor pressure and change in saturation vapor pressure
% with respect to temperature. Polynomial approximations are from:
% Flatau et al. (1992) Polynomial fits to saturation vapor pressure.
% Journal of Applied Meteorology 31:1507-1513. Input temperature is Celsius.
% --- For water vapor (temperature range is 0C to 100C)
a0 = 6.11213476; b0 = 0.444017302;
a1 = 0.444007856; b1 = 0.286064092e-01;
a2 = 0.143064234e-01; b2 = 0.794683137e-03;
a3 = 0.264461437e-03; b3 = 0.121211669e-04;
a4 = 0.305903558e-05; b4 = 0.103354611e-06;
a5 = 0.196237241e-07; b5 = 0.404125005e-09;
a6 = 0.892344772e-10; b6 = -0.788037859e-12;
a7 = -0.373208410e-12; b7 = -0.114596802e-13;
a8 = 0.209339997e-15; b8 = 0.381294516e-16;
% --- For ice (temperature range is -75C to 0C)
c0 = 6.11123516; d0 = 0.503277922;
c1 = 0.503109514; d1 = 0.377289173e-01;
c2 = 0.188369801e-01; d2 = 0.126801703e-02;
c3 = 0.420547422e-03; d3 = 0.249468427e-04;
c4 = 0.614396778e-05; d4 = 0.313703411e-06;
c5 = 0.602780717e-07; d5 = 0.257180651e-08;
c6 = 0.387940929e-09; d6 = 0.133268878e-10;
c7 = 0.149436277e-11; d7 = 0.394116744e-13;
c8 = 0.262655803e-14; d8 = 0.498070196e-16;
% --- Limit temperature to -75C to 100C
tc = min(tc, 100);
tc = max(tc, -75);
% --- Saturation vapor pressure (esat, mb) and derivative (desat, mb)
if (tc >= 0)
esat = a0 + tc*(a1 + tc*(a2 + tc*(a3 + tc*(a4 ...
+ tc*(a5 + tc*(a6 + tc*(a7 + tc*a8)))))));
desat = b0 + tc*(b1 + tc*(b2 + tc*(b3 + tc*(b4 ...
+ tc*(b5 + tc*(b6 + tc*(b7 + tc*b8)))))));
else
esat = c0 + tc*(c1 + tc*(c2 + tc*(c3 + tc*(c4 ...
+ tc*(c5 + tc*(c6 + tc*(c7 + tc*c8)))))));
desat = d0 + tc*(d1 + tc*(d2 + tc*(d3 + tc*(d4 ...
+ tc*(d5 + tc*(d6 + tc*(d7 + tc*d8)))))));
end
% --- Convert from mb to Pa
esat = esat * 100;
desat = desat * 100;
StomataEfficiency.m | View on GitHub
function [flux, val] = StomataEfficiency (physcon, atmos, leaf, flux, gs_val)
% Stomatal efficiency check to determine maximum gs. For the stomatal conductance
% gs_val, calculate photosynthesis for an increase in stomatal conductance equal
% to "delta". The returned value is positive if this increase produces a change
% in photosynthesis > iota*vpd*delta. The returned value is negative if the increase
% produces a change in photosynthesis < iota*vpd*delta.
% --- Specify "delta" as a small difference in gs (mol H2O/m2/s)
delta = 0.001;
% -- Calculate photosynthesis at lower gs (gs_val - delta)
% gs2 - lower value for gs (mol H2O/m2/s)
% an2 - leaf photosynthesis at gs2 (umol CO2/m2/s)
gs2 = gs_val - delta;
flux.gs = gs2;
[flux] = LeafPhotosynthesis (physcon, atmos, leaf, flux);
an2 = flux.an;
% -- Calculate photosynthesis at higher gs (gs_val)
% gs1 - higher value for gs (mol H2O/m2/s)
% an1 - leaf photosynthesis at gs1 (umol CO2/m2/s)
gs1 = gs_val;
flux.gs = gs1;
[flux] = LeafPhotosynthesis (physcon, atmos, leaf, flux);
an1 = flux.an;
% --- Efficiency check: val < 0 when d(An) / d(gs) < iota * vpd
val = (an1 - an2) - leaf.iota * delta * (flux.vpd / atmos.patm);
StomataOptimization.m | View on GitHub
function [flux] = StomataOptimization (physcon, atmos, leaf, flux)
% Leaf temperature, energy fluxes, photosynthesis, and stomatal conductance
% with water-use efficiency stomatal optimization
% --- Low and high initial estimates for gs (mol H2O/m2/s)
gs1 = 0.002;
gs2 = 2.0;
% --- Check for minimum stomatal conductance linked to low light
% based on the efficiency check for gs1 and gs2 (check1, check2)
[flux, check1] = StomataEfficiency (physcon, atmos, leaf, flux, gs1);
[flux, check2] = StomataEfficiency (physcon, atmos, leaf, flux, gs2);
if (check1 * check2 < 0)
% Calculate gs using the function StomataEfficiency to iterate gs
% to an accuracy of tol (mol H2O/m2/s)
tol = 0.004;
func_name = 'StomataEfficiency';
[flux, root] = brent_root (func_name, physcon, atmos, leaf, flux, gs1, gs2, tol);
flux.gs = root;
else
% Low light. Set gs to minimum conductance
flux.gs = 0.002;
end
% --- Leaf fluxes for this gs
[flux] = LeafPhotosynthesis (physcon, atmos, leaf, flux);
[flux] = LeafTranspiration (physcon, atmos, flux);
Output
Figures
Figure 1
Text
light_response.txt | View on GitHub | View raw