Biogeochemical Model

% Supplemental program 17.1

% -----------------------------
% Example of a simple BGC model
% -----------------------------

% --------------
% Initialization
% --------------

% --- number of pools

npool = 9;

% --- NPP (gC/m2/day)

U = 1000 / 365;

% --- NPP partitioning: B(i,1) = NPP partitioning to pool i

B(1,1) = 0.25;            % leaf
B(2,1) = 0.55;            % fine root
B(3,1) = 0.20;            % wood
B(4,1) = 0;               % metabolic litter
B(5,1) = 0;               % structural litter
B(6,1) = 0;               % coarse woody debris
B(7,1) = 0;               % fast SOM
B(8,1) = 0;               % slow SOM
B(9,1) = 0;               % passive SOM

% --- base turnover rate: K(i,i) = base turnover rate for pool i (/day)

K = zeros(npool,npool);   % zero array elements

K(1,1) = 1.12 / 365;      % leaf
K(2,2) = 0.10 / 365;      % fine root
K(3,3) = 0.025 / 365;     % wood
K(4,4) = 10.0 / 365;      % metabolic litter
K(5,5) = 0.95 / 365;      % structural litter
K(6,6) = 0.49 / 365;      % coarse woody debris
K(7,7) = 1.97 / 365;      % fast SOM
K(8,8) = 0.108 / 365;     % slow SOM
K(9,9) = 0.0024 / 365;    % passive SOM

% --- carbon transfer matrix: A(i,j) = fractional carbon flow from pool j that enters pool i

A = zeros(npool,npool);

A(1,1) = -1;
A(2,2) = -1;
A(3,3) = -1;
A(4,4) = -1;
A(5,5) = -1;
A(6,6) = -1;
A(7,7) = -1;
A(8,8) = -1;
A(9,9) = -1;

A(4,1) = 0.67;
A(5,1) = 0.33;
A(4,2) = 0.58;
A(5,2) = 0.42;
A(6,3) = 1.00;
A(7,4) = 0.45;
A(7,5) = 0.36;
A(8,5) = 0.14;
A(7,6) = 0.24;
A(8,6) = 0.28;
A(8,7) = 0.39;
A(9,7) = 0.006;
A(9,8) = 0.003;

% --- environmental scalar: xi(i,i) = environmental scalar for pool i

xi = zeros(npool,npool);

xi(1,1) = 1.01;
xi(2,2) = 1.00;
xi(3,3) = 1.00;
xi(4,4) = 0.40;
xi(5,5) = 0.40;
xi(6,6) = 0.40;
xi(7,7) = 0.40;
xi(8,8) = 0.40;
xi(9,9) = 0.40;

% --- initial pool size: C(i,1) = carbon for pool i (g C/m2)

C = zeros(npool,1);

% ------------------
% Time stepping loop
% ------------------

% --- length of time step (days)

dt = 1;

% --- number of years to simulate 

nyears = 10000;

% --- days per month

ndays = [31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31];

% --- initialize step counter

nstep = 0;

% --- advance time

for year = 1:nyears
   for month = 1:12
      for day = 1:ndays(month)

         nstep = nstep + 1;       % step counter
         cumyear = nstep / 365;   % cumulative year

         % calculate pool increment dC for each pool - this is the full caculation for each pool

%        dC(1,1) = U * B(1,1) - xi(1,1) * K(1,1) * C(1,1);
%        dC(2,1) = U * B(2,1) - xi(2,2) * K(2,2) * C(2,1);
%        dC(3,1) = U * B(3,1) - xi(3,3) * K(3,3) * C(3,1);

%        dC(4,1) = A(4,1)*xi(1,1)*K(1,1)*C(1,1) + A(4,2)*xi(2,2)*K(2,2)*C(2,1) - xi(4,4)*K(4,4)*C(4,1);
%        dC(5,1) = A(5,1)*xi(1,1)*K(1,1)*C(1,1) + A(5,2)*xi(2,2)*K(2,2)*C(2,1) - xi(5,5)*K(5,5)*C(5,1);
%        dC(6,1) = xi(3,3)*K(3,3)*C(3,1) - xi(6,6)*K(6,6)*C(6,1);

%        dC(7,1) = A(7,4)*xi(4,4)*K(4,4)*C(4,1) + A(7,5)*xi(5,5)*K(5,5)*C(5,1) ...
%                + A(7,6)*xi(6,6)*K(6,6)*C(6,1) - xi(7,7)*K(7,7)*C(7,1);

%        dC(8,1) = A(8,5)*xi(5,5)*K(5,5)*C(5,1) + A(8,6)*xi(6,6)*K(6,6)*C(6,1) ...
%                + A(8,7)*xi(7,7)*K(7,7)*C(7,1) - xi(8,8)*K(8,8)*C(8,1);

%        dC(9,1) = A(9,7)*xi(7,7)*K(7,7)*C(7,1) + A(9,8)*xi(8,8)*K(8,8)*C(8,1) ...
%                - xi(9,9)*K(9,9)*C(9,1);

         % ... or calculate pool increment dC for each pool i - this is the generalized calculation

         for i = 1:npool
            dC(i,1) = U * B(i,1) - xi(i,i) * K(i,i) * C(i,1);
            for j = 1:npool
               if (j ~= i)
                  dC(i,1) = dC(i,1) + A(i,j) * xi(j,j) * K(j,j) * C(j,1);
               end
            end
         end

         % ... or use matrix algebra: dC = B * U + A * xi * K * C

%        dC = B * U + A * xi * K * C;

         % heterotrophic respiration

%        RH = (1 - A(7,4))          * xi(4,4) * K(4,4) * C(4,1) ...
%           + (1 - A(7,5) - A(8,5)) * xi(5,5) * K(5,5) * C(5,1) ...
%           + (1 - A(7,6) - A(8,6)) * xi(6,6) * K(6,6) * C(6,1) ...
%           + (1 - A(8,7) - A(9,7)) * xi(7,7) * K(7,7) * C(7,1) ...
%           + (1 - A(9,8))          * xi(8,8) * K(8,8) * C(8,1) ...
%           +                         xi(9,9) * K(9,9) * C(9,1);

         % ... or this is the generalized calculation

         RH = xi(9,9) * K(9,9) * C(9,1);
         for j = 4:8
            suma = 0;
            for i = 4:9
               if (i ~= j)
                  suma = suma + A(i,j);
               end
            end
            RH = RH + (1 - suma) * xi(j,j) * K(j,j) * C(j,1);
         end

         % update pools

         for i = 1:npool
            C(i,1) = C(i,1) + dC(i,1) * dt;
         end

         vegc = C(1,1) + C(2,1) + C(3,1);     % vegetation: leaf + root + wood
         litc = C(4,1) + C(5,1);              % litter: metabolic + structural
         cwdc = C(6,1);                       % coarse woody debris
         somc = C(7,1) + C(8,1) + C(9,1);     % soil organic matter: fast + slow + passive
         totc = vegc + litc + cwdc + somc;    % total carbon

         % balance check

         dCtot = 0;
         for i = 1:npool
            dCtot = dCtot + dC(i,1);
         end

         err = U - (RH + dCtot);
         if (abs(err) > 1e-12)
            fprintf('err = %15.5f\n',err)
            error ('BALANCE CHECK ERROR')
         end

      end
   end

   % save annual output for graphing

   x1(year) = cumyear;
   y1(year) = vegc;
   y2(year) = litc;
   y3(year) = cwdc;
   y4(year) = somc;
   y5(year) = totc;

   fprintf('year = %8.1f\n',cumyear)

end

% ----------------------
% write final pools
% ----------------------

fprintf('%8.1f %15.5f %15.5f %15.5f %15.5f %15.5f\n',cumyear,vegc,litc,cwdc,somc,totc)

% ----------------------
% equilibrium pool sizes
% ----------------------

C_eq = -U * ((A * xi * K) \ B);

vegc = C_eq(1,1) + C_eq(2,1) + C_eq(3,1);
litc = C_eq(4,1) + C_eq(5,1);
cwdc = C_eq(6,1);
somc = C_eq(7,1) + C_eq(8,1) + C_eq(9,1);
totc = vegc + litc + cwdc + somc;

fprintf('%8.1f %15.5f %15.5f %15.5f %15.5f %15.5f\n',cumyear,vegc,litc,cwdc,somc,totc)

% ----------------------
% graph data
% ----------------------

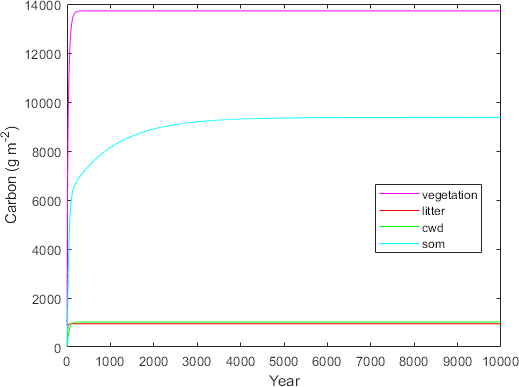
plot(x1,y1,'m-',x1,y2,'r-',x1,y3,'g-',x1,y4,'c-')
xlabel('Year')
ylabel('Carbon (g m^{-2})')
legend('vegetation','litter','cwd','som','Location','best')

% ----------------------------------
% Write formated output to text file
% ----------------------------------

data = [x1; y1; y2; y3; y4; y5];
fileID = fopen('data.txt','w');
fprintf(fileID,'%8s %15s %15s %15s %15s %15s\n','year','vegc','litc','cwdc','somc','totc');
fprintf(fileID,'%8.1f %15.5f %15.5f %15.5f %15.5f %15.5f\n',data);
fclose(fileID);