Radiative Transfer
Table of contents
Code
Main program
sp_14_03.m | View on GitHub
% Supplemental program 14.3
% --------------------------------------------
% Calculate and graph light profiles in canopy
% --------------------------------------------
% --- Model parameters
params.numrad = 2; % Number of wavebands (visible, near-infrared)
params.vis = 1; % Array index for visible waveband
params.nir = 2; % Array index for near-infrared waveband
params.sun = 1; % Array index for sunlit leaf
params.sha = 2; % Array index for shaded leaf
params.npts = 1; % Number of grid points to process
% --- Model options
light = 'Norman'; % Use Norman radiative transfer
% light = 'Goudriaan'; % Use Goudriaan radiative transfer
% light = 'TwoStream'; % Use two-stream approximation radiative transfer
canopy_type = 'dense'; % High leaf area index
% canopy_type = 'sparse'; % Low leaf area index
% --- Define plant canopy
for p = 1:params.npts
% Set canopy LAI, layer LAI increment, and number of layers
switch canopy_type
case 'dense'
lai_inc = 0.1; % Leaf area index for each layer
canopy.lai(p) = 6; % Leaf area index of canopy (m2/m2)
case 'sparse'
lai_inc = 0.05; % Leaf area index for each layer
canopy.lai(p) = 1; % Leaf area index of canopy (m2/m2)
end
canopy.nveg(p) = round(canopy.lai(p) / lai_inc); % Number of leaf layers in canopy
% Minimum number of layers for Norman radiation
switch light
case 'Norman'
if (canopy.nveg(p) < 10)
canopy.nveg(p) = 10;
lai_inc = canopy.lai(p) / canopy.nveg(p);
end
end
% Set array indices for canopy layers
canopy.nsoi(p) = 1; % First layer is soil
canopy.nbot(p) = canopy.nsoi(p) + 1; % Bottom leaf layer
canopy.ntop(p) = canopy.nbot(p) + canopy.nveg(p) - 1; % Top leaf layer
% Set LAI of each layer
for iv = canopy.nbot(p):canopy.ntop(p)
canopy.dlai(p,iv) = lai_inc;
end
% Cumulative leaf area index (from canopy top) at mid-layer
for iv = canopy.ntop(p): -1: canopy.nbot(p)
if (iv == canopy.ntop(p))
canopy.sumlai(p,iv) = 0.5 * canopy.dlai(p,iv);
else
canopy.sumlai(p,iv) = canopy.sumlai(p,iv+1) + canopy.dlai(p,iv);
end
end
% Clumping index
canopy.clumpfac(p) = 1;
end
% --- Atmospheric solar radiation. Solar radiation is given as a unit of visible radiation
% and a unit of near-infrared radiation, both split into direct and diffuse components.
for p = 1:params.npts
atmos.solar_zenith(p) = 30 * (pi / 180); % Solar zentih angle (radians)
atmos.swskyb(p,params.vis) = 0.8; % Direct beam solar radiation for visible waveband (W/m2)
atmos.swskyd(p,params.vis) = 0.2; % Diffuse solar radiation for visible waveband (W/m2)
atmos.swskyb(p,params.nir) = 0.8; % Direct beam solar radiation for near-infrared waveband (W/m2)
atmos.swskyd(p,params.nir) = 0.2; % Diffuse solar radiation for near-infrared waveband (W/m2)
end
% --- Leaf optical properties
for p = 1:params.npts
rho(p,params.vis) = 0.10; % Leaf reflectance (visible)
rho(p,params.nir) = 0.45; % Leaf reflectance (near-infrared)
tau(p,params.vis) = 0.05; % Leaf transmittance (visible)
tau(p,params.nir) = 0.25; % Leaf transmittance (near-infrared)
for ib = 1:params.numrad
omega(p,ib) = rho(p,ib) + tau(p,ib); % Leaf scattering coefficient for canopy
end
end
% --- Soil albedo
for p = 1:params.npts
flux.albsoib(p,params.vis) = 0.1; % Direct beam albedo of ground (visible)
flux.albsoid(p,params.vis) = flux.albsoib(p,params.vis); % Diffuse albedo of ground (visible)
flux.albsoib(p,params.nir) = 0.2; % Direct beam albedo of ground (near-infrared)
flux.albsoid(p,params.nir) = flux.albsoib(p,params.nir); % Diffuse albedo of ground near-infrared)
end
% --- Direct beam extinction coefficient
% xl - departure of leaf angle from spherical orientation
xl = 0.00;
% Kb - direct beam extinction coefficient for canopy
for p = 1:params.npts
% -0.4 <= xl <= 0.6
chil(p) = min(max(xl, -0.4), 0.6);
% Prevent near-zero xl for two-stream radiation
switch light
case 'TwoStream'
if (abs(chil(p)) <= 0.01)
chil(p) = 0.01;
end
end
% Terms in Ross-Goudriaan function for gdir
phi1(p) = 0.5 - 0.633 * chil(p) - 0.330 * chil(p)*chil(p);
phi2(p) = 0.877 * (1 - 2 * phi1(p));
% Relative projected area of leaf in the direction of solar beam
cosz = cos(atmos.solar_zenith(p));
gdir(p) = phi1(p) + phi2(p) * cosz;
% Direct beam extinction coefficient
Kb(p) = gdir(p) / cosz;
% Prevent large Kb at low sun angle
Kb(p) = min(Kb(p), 20);
end
% --- Sunlit and shaded portions of canopy
for p = 1:params.npts
% Sunlit and shaded fraction of leaf layer
for iv = canopy.nbot(p):canopy.ntop(p)
flux.fracsun(p,iv) = canopy.clumpfac(p) * exp(-Kb(p) * canopy.sumlai(p,iv) * canopy.clumpfac(p));
flux.fracsha(p,iv) = 1 - flux.fracsun(p,iv);
end
% Sunlit and shaded leaf area index for canopy
laisun(p) = (1 - exp(-Kb(p) * canopy.lai(p) * canopy.clumpfac(p))) / Kb(p);
laisha(p) = canopy.lai(p) - laisun(p);
end
% --- Unique parameters for Norman radiative transfer
% tb - exponential transmittance of direct beam radiation through a single leaf layer
for p = 1:params.npts
for iv = canopy.nbot(p):canopy.ntop(p)
tb(p,iv) = exp(-Kb(p) * canopy.dlai(p,iv) * canopy.clumpfac(p));
end
end
% td - exponential transmittance of diffuse radiation through a single leaf layer
% with thickness dlai, estimated for nine sky angles in increments of 10 degrees
for p = 1:params.npts
for iv = canopy.nbot(p):canopy.ntop(p)
td(p,iv) = 0;
for j = 1:9
% Sky angles (5, 15, 25, 35, 45, 55, 65, 75, 85)
angle = (5 + (j - 1) * 10) * pi / 180;
% Relative projected area of leaf in the direction of sky angle
gdirj = phi1(p) + phi2(p) * cos(angle);
% Sum transmittance
td(p,iv) = td(p,iv) ...
+ exp(-gdirj / cos(angle) * canopy.dlai(p,iv) * canopy.clumpfac(p)) * sin(angle) * cos(angle);
end
td(p,iv) = td(p,iv) * 2 * (10 * pi / 180);
end
end
% tbcum - direct beam transmittance uses cumulative lai above layer i to
% give unscattered direct beam onto layer i
for p = 1:params.npts
cumlai = 0;
iv = canopy.ntop(p);
tbcum(p,iv) = 1;
for iv = canopy.ntop(p): -1: canopy.nbot(p)
cumlai = cumlai + canopy.dlai(p,iv);
tbcum(p,iv-1) = exp(-Kb(p) * cumlai * canopy.clumpfac(p));
end
end
% --- Unique parameters for Goudriaan radiative transfer
% Kd - diffuse extinction coefficient for canopy, estimated for nine sky angles
% in increments of 10 degrees
for p = 1:params.npts
Kd(p) = 0;
for j = 1:9
% Sky angles (5, 15, 25, 35, 45, 55, 65, 75, 85)
angle = (5 + (j - 1) * 10) * pi / 180;
% Relative projected area of leaf in the direction of sky angle
gdirj = phi1(p) + phi2(p) * cos(angle);
% Sum transmittance
Kd(p) = Kd(p) + exp(-gdirj / cos(angle) * canopy.lai(p) * canopy.clumpfac(p)) * sin(angle) * cos(angle);
end
Kd(p) = Kd(p) * 2 * (10 * pi / 180);
% Convert transmittance to extinction coefficient
if (canopy.lai(p) > 0)
Kd(p) = -log(Kd(p)) / (canopy.lai(p) * canopy.clumpfac(p));
else
Kd(p) = 0;
end
end
for ib = 1:params.numrad
for p = 1:params.npts
% Adjust Kb and Kd for scattering
Kbm(p,ib) = Kb(p) * sqrt(1 - omega(p,ib));
Kdm(p,ib) = Kd(p) * sqrt(1 - omega(p,ib));
% albvegh - vegetation albedo for horizontal leaves
albvegh = (1 - sqrt(1 - omega(p,ib))) / (1 + sqrt(1 - omega(p,ib)));
% albvegb - direct beam vegetation albedo for non-horizontal leaves
albvegb = 2 * Kb(p) / (Kb(p) + Kd(p)) * albvegh;
% albvegd - diffuse vegetation albedo for non-horizontal leaves, calculated by summing albedo over 9 sky angles
albvegd = 0;
for j = 1:9
% Sky angles (5, 15, 25, 35, 45, 55, 65, 75, 85)
angle = (5 + (j - 1) * 10) * pi / 180;
% Relative projected area of leaf in the direction of sky angle
gdirj = phi1(p) + phi2(p) * cos(angle);
% Kb for sky angle j
Kbj = gdirj / cos(angle);
% Direct beam albedo for sky angle j
albvegbj = 2 * Kbj / (Kbj + Kd(p)) * albvegh;
% Sum albedo
albvegd = albvegd + albvegbj * sin(angle) * cos(angle);
end
albvegd = albvegd * 2 * (10 * pi / 180);
% Effective canopy albedo, including soil
% albcanb - direct beam albedo above canopy
% albcand - diffuse albedo above canopy
albcanb(p,ib) = albvegb ...
+ (flux.albsoib(p,ib) - albvegb) * exp(-2 * Kbm(p,ib) * canopy.lai(p) * canopy.clumpfac(p));
albcand(p,ib) = albvegd ...
+ (flux.albsoid(p,ib) - albvegd) * exp(-2 * Kdm(p,ib) * canopy.lai(p) * canopy.clumpfac(p));
end
end
% --- Two-stream parameters
for p = 1:params.npts
% avmu - average inverse diffuse optical depth per unit leaf area
avmu(p) = ( 1 - phi1(p)/phi2(p) * log((phi1(p)+phi2(p))/phi1(p)) ) / phi2(p);
% Upscatter parameters
for ib = 1:params.numrad
% betad - upscatter parameter for diffuse radiation
betad(p,ib) = 0.5 / omega(p,ib) * ( rho(p,ib) + tau(p,ib) + (rho(p,ib)-tau(p,ib)) * ((1+chil(p))/2)^2 );
% betab - upscatter parameter for direct beam radiation
cosz = cos(atmos.solar_zenith(p));
tmp0 = gdir(p) + phi2(p) * cosz;
tmp1 = phi1(p) * cosz;
tmp2 = 1 - tmp1/tmp0 * log((tmp1+tmp0)/tmp1);
asu = 0.5 * omega(p,ib) * gdir(p) / tmp0 * tmp2;
betab(p,ib) = (1 + avmu(p)*Kb(p)) / (omega(p,ib)*avmu(p)*Kb(p)) * asu;
end
end
% --- Light profile through canopy
switch light
case 'Norman'
[flux] = NormanRadiation (rho, tau, omega, td, tb, tbcum, params, canopy, atmos, flux);
case 'Goudriaan'
[flux] = GoudriaanRadiation (omega, Kb, Kbm, Kdm, albcanb, albcand, params, canopy, atmos, flux);
case 'TwoStream'
[flux] = TwoStreamRadiation (omega, avmu, betad, betab, Kb, params, canopy, atmos, flux);
end
% Absorbed PAR per unit sunlit and shaded leaf area (umol photon/m2 leaf/s)
for p = 1:params.npts
for iv = canopy.nbot(p):canopy.ntop(p)
flux.apar(p,iv,params.sun) = flux.swleaf(p,iv,params.sun,params.vis) * 4.6;
flux.apar(p,iv,params.sha) = flux.swleaf(p,iv,params.sha,params.vis) * 4.6;
end
end
% --- Write formatted output to file, from top layer to bottom layer
p = 1;
for iv = canopy.ntop(p): -1: canopy.nbot(p)
j = iv - 1;
k = canopy.nveg(p) - j + 2;
a1(j) = j;
a2(j) = canopy.sumlai(p,k);
a3(j) = flux.swleaf(p,k,params.sun,params.vis);
a4(j) = flux.swleaf(p,k,params.sha,params.vis);
a5(j) = flux.swleaf(p,k,params.sun,params.nir);
a6(j) = flux.swleaf(p,k,params.sha,params.nir);
end
A = [a1; a2; a3; a4; a5; a6];
fileID = fopen('data.txt','w');
fprintf(fileID,'%12s %12s %12s %12s %12s %12s\n','layer','lai','sun','sha','sun','sha');
fprintf(fileID,'%12.0f %12.4f %12.6f %12.6f %12.6f %12.6f\n', A);
fclose(fileID);
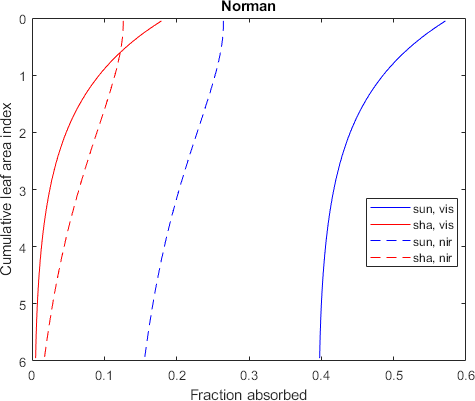
% --- Make graph
plot(a3,a2,'b-',a4,a2,'r-',a5,a2,'b--',a6,a2,'r--')
set(gca,'YDir','reverse')
title(light)
xlabel('Fraction absorbed')
ylabel('Cumulative leaf area index')
legend('sun, vis','sha, vis','sun, nir','sha, nir','Location','best')
Aux. programs
GoudriaanRadiation.m | View on GitHub
function [flux] = GoudriaanRadiation (omega, Kb, Kbm, Kdm, albcanb, albcand, params, canopy, atmos, flux)
% Compute solar radiation transfer through canopy using Goudriaan parameterization.
% Radiative transfer of Goudriaan (1977), as described by Goudriaan and van Laar
% (1994) and implemented in the plant canopy models of Spitters (1986),
% de Pury and Farquhar (1997), Wang and Leuning (1998), and Wang (2003).
% This uses the multilayer form of the equations, with constant optical
% properties through the canopy.
% -----------------------------------------------------------------------
% Input
% omega ! Leaf scattering coefficient for canopy
% Kb ! Direct beam extinction coefficient for canopy
% Kbm ! Direct beam extinction coefficient for canopy adjusted for scattering
% Kdm ! Diffuse extinction coefficient for canopy adjusted for scattering
% albcanb ! Direct beam albedo above canopy
% albcand ! Diffuse albedo above canopy
% params.numrad ! Number of wavebands
% params.npts ! Number of grid points to process
% params.sun ! Index for sunlit leaf
% params.sha ! Index for shaded leaf
% canopy.ntop ! Index for top leaf layer
% canopy.nbot ! Index for bottom leaf layer
% canopy.dlai ! Layer leaf area index (m2/m2)
% canopy.lai ! Leaf area index of canopy (m2/m2)
% canopy.sumlai ! Cumulative leaf area index for canopy layer (m2/m2)
% canopy.clumpfac ! Leaf clumping index
% atmos.swskyb ! Atmospheric direct beam solar radiation (W/m2)
% atmos.swskyd ! Atmospheric diffuse solar radiation (W/m2)
% flux.fracsun ! Sunlit fraction of canopy layer
% flux.fracsha ! Shaded fraction of canopy layer
%
% Output
% flux.swleaf ! Leaf absorbed solar radiation (W/m2 leaf)
% flux.swveg ! Absorbed solar radiation, vegetation (W/m2)
% flux.swvegsun ! Absorbed solar radiation, sunlit canopy (W/m2)
% flux.swvegsha ! Absorbed solar radiation, shaded canopy (W/m2)
% flux.swsoi ! Absorbed solar radiation, ground (W/m2)
% flux.albcan ! Albedo above canopy
% -----------------------------------------------------------------------
% --- Process each waveband (ib) for each grid point (p)
for ib = 1:params.numrad
for p = 1:params.npts
% Zero terms that are summed over all layers
icsun = 0;
icsha = 0;
icshad = 0;
icshabs = 0;
icsund = 0;
icsunbs = 0;
icsunb = 0;
% Process each canopy layer (iv)
for iv = canopy.nbot(p):canopy.ntop(p)
% --- Calculate leaf fluxes. Fluxes are per unit leaf area (W/m2 leaf)
% ild - absorbed diffuse flux per unit leaf area at cumulative LAI,
% average for all leaves (J / m2 leaf / s)
ild = (1 - albcand(p,ib)) * atmos.swskyd(p,ib) * Kdm(p,ib) * canopy.clumpfac(p) ...
* exp(-Kdm(p,ib) * canopy.sumlai(p,iv) * canopy.clumpfac(p));
% ilb - absorbed direct beam flux (total with scattering) per unit leaf area
% at cumulative LAI, average for all leaves (J / m2 leaf / s)
ilb = (1 - albcanb(p,ib)) * atmos.swskyb(p,ib) * Kbm(p,ib) * canopy.clumpfac(p) ...
* exp(-Kbm(p,ib) * canopy.sumlai(p,iv) * canopy.clumpfac(p));
% ilbb - absorbed direct beam flux (unscattered direct component) per unit leaf area
% at cumulative LAI, average for all leaves (J / m2 leaf / s)
ilbb = (1 - omega(p,ib)) * atmos.swskyb(p,ib) * Kb(p) * canopy.clumpfac(p) ...
* exp(-Kb(p) * canopy.sumlai(p,iv) * canopy.clumpfac(p));
% ilbs - absorbed direct beam flux (scattered direct component) per unit leaf area
% at cumulative LAI, average for all leaves (J / m2 leaf / s)
ilbs = ilb - ilbb;
% ilsha - total absorbed flux (shaded leaves) per unit shaded leaf area
% at cumulative LAI (J / m2 leaf / s)
ilsha = ild + ilbs;
% ilsun - total absorbed flux (sunlit leaves) per unit sunlit leaf area
% at cumulative LAI (J / m2 leaf / s)
ilsun = ilsha + Kb(p) * (1 - omega(p,ib)) * atmos.swskyb(p,ib);
% Save solar radiation absorbed by sunlit and shaded leaves
flux.swleaf(p,iv,params.sun,ib) = ilsun;
flux.swleaf(p,iv,params.sha,ib) = ilsha;
% --- Canopy summation and soil absorption. Fluxes are per unit ground area (W/m2 ground area)
% icsun - absorbed solar radiation, sunlit canopy (W/m2)
% icsha - absorbed solar radiation, shaded canopy (W/m2)
icsun = icsun + ilsun * flux.fracsun(p,iv) * canopy.dlai(p,iv);
icsha = icsha + ilsha * flux.fracsha(p,iv) * canopy.dlai(p,iv);
% icshad - diffuse radiation absorbed by shaded leaves (W/m2)
% icshabs - scattered direct beam radiation absorbed by shaded leaves (W/m2)
icshad = icshad + ild * flux.fracsha(p,iv) * canopy.dlai(p,iv);
icshabs = icshabs + ilbs * flux.fracsha(p,iv) * canopy.dlai(p,iv);
% icsund - diffuse radiation absorbed by sunlit leaves (W/m2)
% icsunbs - scattered direct beam radiation absorbed by sunlit leaves (W/m2)
% icsunb - direct beam radiation absorbed by sunlit leaves (W/m2)
icsund = icsund + ild * flux.fracsun(p,iv) * canopy.dlai(p,iv);
icsunbs = icsunbs + ilbs * flux.fracsun(p,iv) * canopy.dlai(p,iv);
icsunb = icsunb + Kb(p) * (1 - omega(p,ib)) * atmos.swskyb(p,ib) * flux.fracsun(p,iv) * canopy.dlai(p,iv);
end
% Solar radiation absorbed by vegetation (W/m2)
sabv = icsun + icsha;
% Solar radiation absorbed by ground (W/m2)
sabg = atmos.swskyb(p,ib) * (1 - albcanb(p,ib)) * exp(-Kbm(p,ib)*canopy.lai(p)*canopy.clumpfac(p)) + ...
atmos.swskyd(p,ib) * (1 - albcand(p,ib)) * exp(-Kdm(p,ib)*canopy.lai(p)*canopy.clumpfac(p));
% Conservation check: absorbed = incoming - outgoing
% This is not valid, because the numerical integration of leaf fluxes does not equal the analytical
% solution (unless dlai is very small)
suminc = atmos.swskyb(p,ib) + atmos.swskyd(p,ib);
sumabs = sabv + sabg;
sumref = atmos.swskyb(p,ib) * albcanb(p,ib) + atmos.swskyd(p,ib) * albcand(p,ib);
err = suminc - (sumref + sumabs);
err = 0;
if (abs(err) > 1e-03)
fprintf('err = %15.5f\n',err)
fprintf('suminc = %15.5f\n',suminc)
fprintf('sumref = %15.5f\n',sumref)
fprintf('sumabs = %15.5f\n',sumabs)
error ('GoudriaanRadiation: Solar radiation conservation error')
end
% --- Save necessary radiative fluxes
% Albedo
suminc = atmos.swskyb(p,ib) + atmos.swskyd(p,ib);
sumref = atmos.swskyb(p,ib) * albcanb(p,ib) + atmos.swskyd(p,ib) * albcand(p,ib);
if (suminc > 0)
flux.albcan(p,ib) = sumref / suminc;
else
flux.albcan(p,ib) = 0;
end
% Solar radiation absorbed by canopy
flux.swveg(p,ib) = sabv;
flux.swvegsun(p,ib) = icsun;
flux.swvegsha(p,ib) = icsha;
% Solar radiation absorbed by ground (soil)
flux.swsoi(p,ib) = sabg;
end
end
NormanRadiation.m | View on GitHub
function [flux] = NormanRadiation (rho, tau, omega, td, tb, tbcum, params, canopy, atmos, flux)
% Compute solar radiation transfer through canopy using Norman (1979)
% -----------------------------------------------------------------------
% Input
% rho ! Leaf reflectance
% tau ! Leaf transmittance
% omega ! Leaf scattering coefficient
% td ! Exponential transmittance of diffuse radiation through a single leaf layer
% tb ! Exponential transmittance of direct beam radiation through a single leaf layer
% tbcum ! Cumulative exponential transmittance of direct beam onto a canopy layer
% params.numrad ! Number of wavebands
% params.npts ! Number of grid points to process
% params.sun ! Index for sunlit leaf
% params.sha ! Index for shaded leaf
% canopy.ntop ! Index for top leaf layer
% canopy.nbot ! Index for bottom leaf layer
% canopy.nsoi ! First canopy layer is soil
% canopy.dlai ! Layer leaf area index (m2/m2)
% atmos.swskyb ! Atmospheric direct beam solar radiation (W/m2)
% atmos.swskyd ! Atmospheric diffuse solar radiation (W/m2)
% flux.fracsun ! Sunlit fraction of canopy layer
% flux.fracsha ! Shaded fraction of canopy layer
% flux.albsoib ! Direct beam albedo of ground (soil)
% flux.albsoid ! Diffuse albedo of ground (soil)
%
% Output
% flux.swleaf ! Leaf absorbed solar radiation (W/m2 leaf)
% flux.swveg ! Absorbed solar radiation, vegetation (W/m2)
% flux.swvegsun ! Absorbed solar radiation, sunlit canopy (W/m2)
% flux.swvegsha ! Absorbed solar radiation, shaded canopy (W/m2)
% flux.swsoi ! Absorbed solar radiation, ground (W/m2)
% flux.albcan ! Albedo above canopy
% -----------------------------------------------------------------------
% --- Set up tridiagonal matrix
for ib = 1:params.numrad % Process each waveband
for p = 1:params.npts % Process each grid point
iv = canopy.nsoi(p);
swup(iv) = 0;
swdn(iv) = 0;
for iv = canopy.nbot(p):canopy.ntop(p)
swup(iv) = 0;
swdn(iv) = 0;
end
% There are two equations for each canopy layer and the soil. The first
% equation is the upward flux and the second equation is the downward flux.
m = 0; % Initialize equation index for tridiagonal matrix
% Soil: upward flux
iv = canopy.nsoi(p);
m = m + 1;
a(m) = 0;
b(m) = 1;
c(m) = -flux.albsoid(p,ib);
d(m) = atmos.swskyb(p,ib) * tbcum(p,iv) * flux.albsoib(p,ib);
% Soil: downward flux
refld = (1 - td(p,iv+1)) * rho(p,ib);
trand = (1 - td(p,iv+1)) * tau(p,ib) + td(p,iv+1);
aiv = refld - trand * trand / refld;
biv = trand / refld;
m = m + 1;
a(m) = -aiv;
b(m) = 1;
c(m) = -biv;
d(m) = atmos.swskyb(p,ib) * tbcum(p,iv+1) * (1 - tb(p,iv+1)) * (tau(p,ib) - rho(p,ib) * biv);
% Leaf layers, excluding top layer
for iv = canopy.nbot(p):canopy.ntop(p)-1
% Upward flux
refld = (1 - td(p,iv)) * rho(p,ib);
trand = (1 - td(p,iv)) * tau(p,ib) + td(p,iv);
fiv = refld - trand * trand / refld;
eiv = trand / refld;
m = m + 1;
a(m) = -eiv;
b(m) = 1;
c(m) = -fiv;
d(m) = atmos.swskyb(p,ib) * tbcum(p,iv) * (1 - tb(p,iv)) * (rho(p,ib) - tau(p,ib) * eiv);
% Downward flux
refld = (1 - td(p,iv+1)) * rho(p,ib);
trand = (1 - td(p,iv+1)) * tau(p,ib) + td(p,iv+1);
aiv = refld - trand * trand / refld;
biv = trand / refld;
m = m + 1;
a(m) = -aiv;
b(m) = 1;
c(m) = -biv;
d(m) = atmos.swskyb(p,ib) * tbcum(p,iv+1) * (1 - tb(p,iv+1)) * (tau(p,ib) - rho(p,ib) * biv);
end
% Top canopy layer: upward flux
iv = canopy.ntop(p);
refld = (1 - td(p,iv)) * rho(p,ib);
trand = (1 - td(p,iv)) * tau(p,ib) + td(p,iv);
fiv = refld - trand * trand / refld;
eiv = trand / refld;
m = m + 1;
a(m) = -eiv;
b(m) = 1;
c(m) = -fiv;
d(m) = atmos.swskyb(p,ib) * tbcum(p,iv) * (1 - tb(p,iv)) * (rho(p,ib) - tau(p,ib) * eiv);
% Top canopy layer: downward flux
m = m + 1;
a(m) = 0;
b(m) = 1;
c(m) = 0;
d(m) = atmos.swskyd(p,ib);
% --- Solve tridiagonal equations for fluxes
[u] = tridiagonal_solver (a, b, c, d, m);
% Now copy the solution (u) to the upward (swup) and downward (swdn) fluxes for each layer
% swup - Upward diffuse solar flux above layer
% swdn - Downward diffuse solar flux onto layer
m = 0;
% Soil fluxes
iv = canopy.nsoi(p);
m = m + 1;
swup(iv) = u(m);
m = m + 1;
swdn(iv) = u(m);
% Leaf layer fluxes
for iv = canopy.nbot(p):canopy.ntop(p)
m = m + 1;
swup(iv) = u(m);
m = m + 1;
swdn(iv) = u(m);
end
% --- Compute flux densities
% Absorbed direct beam and diffuse for ground (soil)
iv = canopy.nsoi(p);
direct = atmos.swskyb(p,ib) * tbcum(p,iv) * (1 - flux.albsoib(p,ib));
diffuse = swdn(iv) * (1 - flux.albsoid(p,ib));
flux.swsoi(p,ib) = direct + diffuse;
% Absorbed direct beam and diffuse for each leaf layer and sum
% for all leaf layers
flux.swveg(p,ib) = 0;
flux.swvegsun(p,ib) = 0;
flux.swvegsha(p,ib) = 0;
for iv = canopy.nbot(p):canopy.ntop(p)
% Per unit ground area (W/m2 ground)
direct = atmos.swskyb(p,ib) * tbcum(p,iv) * (1 - tb(p,iv)) * (1 - omega(p,ib));
diffuse = (swdn(iv) + swup(iv-1)) * (1 - td(p,iv)) * (1 - omega(p,ib));
% Absorbed solar radiation for shaded and sunlit portions of leaf layer
% per unit ground area (W/m2 ground)
sun = diffuse * flux.fracsun(p,iv) + direct;
shade = diffuse * flux.fracsha(p,iv);
% Convert to per unit sunlit and shaded leaf area (W/m2 leaf)
flux.swleaf(p,iv,params.sun,ib) = sun / (flux.fracsun(p,iv) * canopy.dlai(p,iv));
flux.swleaf(p,iv,params.sha,ib) = shade / (flux.fracsha(p,iv) * canopy.dlai(p,iv));
% Sum fluxes over all leaf layers
flux.swveg(p,ib) = flux.swveg(p,ib) + (direct + diffuse);
flux.swvegsun(p,ib) = flux.swvegsun(p,ib) + sun;
flux.swvegsha(p,ib) = flux.swvegsha(p,ib) + shade;
end
% --- Albedo
incoming = atmos.swskyb(p,ib) + atmos.swskyd(p,ib);
reflected = swup(canopy.ntop(p));
if (incoming > 0)
flux.albcan(p,ib) = reflected / incoming;
else
flux.albcan(p,ib) = 0;
end
% --- Conservation check
% Total radiation balance: absorbed = incoming - outgoing
suminc = atmos.swskyb(p,ib) + atmos.swskyd(p,ib);
sumref = flux.albcan(p,ib) * (atmos.swskyb(p,ib) + atmos.swskyd(p,ib));
sumabs = suminc - sumref;
err = sumabs - (flux.swveg(p,ib) + flux.swsoi(p,ib));
if (abs(err) > 1e-03)
fprintf('err = %15.5f\n',err)
fprintf('sumabs = %15.5f\n',sumabs)
fprintf('swveg = %15.5f\n',flux.swveg(p,ib))
fprintf('swsoi = %15.5f\n',flux.swsoi(p,ib))
error ('NormanRadiation: Total solar conservation error')
end
% Sunlit and shaded absorption
err = (flux.swvegsun(p,ib) + flux.swvegsha(p,ib)) - flux.swveg(p,ib);
if (abs(err) > 1e-03)
fprintf('err = %15.5f\n',err)
fprintf('swveg = %15.5f\n',flux.swveg(p,ib))
fprintf('swvegsun = %15.5f\n',flux.swvegsun(p,ib))
fprintf('swvegsha = %15.5f\n',flux.swvegsha(p,ib))
error ('NormanRadiation: Sunlit/shade solar conservation error')
end
end % End grid point loop
end % End waveband loop
tridiagonal_solver.m | View on GitHub
function [u] = tridiagonal_solver (a, b, c, d, n)
% Solve for U given the set of equations R * U = D, where U is a vector
% of length N, D is a vector of length N, and R is an N x N tridiagonal
% matrix defined by the vectors A, B, C each of length N. A(1) and
% C(N) are undefined and are not referenced.
%
% |B(1) C(1) ... ... ... |
% |A(2) B(2) C(2) ... ... |
% R = | A(3) B(3) C(3) ... |
% | ... A(N-1) B(N-1) C(N-1)|
% | ... ... A(N) B(N) |
%
% The system of equations is written as:
%
% A_i * U_i-1 + B_i * U_i + C_i * U_i+1 = D_i
%
% for i = 1 to N. The solution is found by rewriting the
% equations so that:
%
% U_i = F_i - E_i * U_i+1
% --- Forward sweep (1 -> N) to get E and F
e(1) = c(1) / b(1);
for i = 2: 1: n-1
e(i) = c(i) / (b(i) - a(i) * e(i-1));
end
f(1) = d(1) / b(1);
for i = 2: 1: n
f(i) = (d(i) - a(i) * f(i-1)) / (b(i) - a(i) * e(i-1));
end
% --- Backward substitution (N -> 1) to solve for U
u(n) = f(n);
for i = n-1: -1: 1
u(i) = f(i) - e(i) * u(i+1);
end
TwoStreamRadiation.m | View on GitHub
function [flux] = TwoStreamRadiation (omega, avmu, betad, betab, Kb, params, canopy, atmos, flux)
% Compute solar radiation transfer through canopy using the two-stream approximation
% -----------------------------------------------------------------------
% Input
% omega ! Leaf scattering coefficient for canopy
% avmu ! Average inverse diffuse optical depth per unit leaf area
% betad ! Upscatter parameter for diffuse radiation
% betab ! Upscatter parameter for direct beam radiation
% Kb ! Optical depth of direct beam per unit leaf area (direct beam extinction coefficient for canopy)
% params.numrad ! Number of wavebands
% params.npts ! Number of grid points to process
% params.sun ! Index for sunlit leaf
% params.sha ! Index for shaded leaf
% canopy.ntop ! Index for top leaf layer
% canopy.nbot ! Index for bottom leaf layer
% canopy.lai ! Leaf area index of canopy (m2/m2)
% canopy.sumlai ! Cumulative leaf area index for canopy layer (m2/m2)
% canopy.dlai ! Layer leaf area index (m2/m2)
% canopy.clumpfac ! Leaf clumping index
% atmos.swskyb ! Atmospheric direct beam solar radiation (W/m2)
% atmos.swskyd ! Atmospheric diffuse solar radiation (W/m2)
% flux.fracsun ! Sunlit fraction of canopy layer
% flux.fracsha ! Shaded fraction of canopy layer
% flux.albsoib ! Direct beam albedo of ground (soil)
% flux.albsoid ! Diffuse albedo of ground (soil)
%
% Output
% flux.swleaf ! Leaf absorbed solar radiation (W/m2 leaf)
% flux.swveg ! Absorbed solar radiation, vegetation (W/m2)
% flux.swvegsun ! Absorbed solar radiation, sunlit canopy (W/m2)
% flux.swvegsha ! Absorbed solar radiation, shaded canopy (W/m2)
% flux.swsoi ! Absorbed solar radiation, ground (W/m2)
% flux.albcan ! Albedo above canopy
% -----------------------------------------------------------------------
% --- Process each waveband for each grid point
for ib = 1:params.numrad
for p = 1:params.npts
% --- Canopy fluxes using total canopy lai
% Common terms
b = (1 - (1 - betad(p,ib)) * omega(p,ib)) / avmu(p);
c = betad(p,ib) * omega(p,ib) / avmu(p);
h = sqrt(b*b - c*c);
u = (h - b - c) / (2 * h);
v = (h + b + c) / (2 * h);
d = omega(p,ib) * Kb(p) * atmos.swskyb(p,ib) / (h*h - Kb(p)*Kb(p));
g1 = (betab(p,ib) * Kb(p) - b * betab(p,ib) - c * (1 - betab(p,ib))) * d;
g2 = ((1 - betab(p,ib)) * Kb(p) + c * betab(p,ib) + b * (1 - betab(p,ib))) * d;
s1 = exp(-h * canopy.lai(p) * canopy.clumpfac(p));
s2 = exp(-Kb(p) * canopy.lai(p) * canopy.clumpfac(p));
% Direct beam radiation
num1 = v * (g1 + g2 * flux.albsoid(p,ib) + flux.albsoib(p,ib) * atmos.swskyb(p,ib)) * s2;
num2 = g2 * (u + v * flux.albsoid(p,ib)) * s1;
den1 = v * (v + u * flux.albsoid(p,ib)) / s1;
den2 = u * (u + v * flux.albsoid(p,ib)) * s1;
n2b = (num1 - num2) / (den1 - den2);
n1b = (g2 - n2b * u) / v;
a1b = -g1 * (1 - s2*s2) / (2 * Kb(p)) + ...
n1b * u * (1 - s2*s1) / (Kb(p) + h) + n2b * v * (1 - s2/s1) / (Kb(p) - h);
a2b = g2 * (1 - s2*s2) / (2 * Kb(p)) - ...
n1b * v * (1 - s2*s1) / (Kb(p) + h) - n2b * u * (1 - s2/s1) / (Kb(p) - h);
% iupwb0 - Direct beam flux scattered upward (reflected) above canopy (W/m2)
% iupwb - Direct beam flux scattered upward at the canopy depth (W/m2)
% idwnb - Direct beam flux scattered downward below canopy (W/m2)
% iabsb - Direct beam flux absorbed by canopy (W/m2)
% iabsb_sun - Direct beam flux absorbed by sunlit canopy (W/m2)
% iabsb_sha - Direct beam flux absorbed by shaded canopy (W/m2)
iupwb0 = -g1 + n1b * u + n2b * v;
iupwb = -g1 * s2 + n1b * u * s1 + n2b * v / s1;
idwnb = g2 * s2 - n1b * v * s1 - n2b * u / s1;
iabsb = atmos.swskyb(p,ib) * (1 - s2) - iupwb0 + iupwb - idwnb;
iabsb_sun = (1 - omega(p,ib)) ...
* ((1 - s2) * atmos.swskyb(p,ib) + 1 / avmu(p) * (a1b + a2b) * canopy.clumpfac(p));
iabsb_sha = iabsb - iabsb_sun;
% Diffuse radiation
num = atmos.swskyd(p,ib) * (u + v * flux.albsoid(p,ib)) * s1;
den1 = v * (v + u * flux.albsoid(p,ib)) / s1;
den2 = u * (u + v * flux.albsoid(p,ib)) * s1;
n2d = num / (den1 - den2);
n1d = -(atmos.swskyd(p,ib) + n2d * u) / v;
a1d = n1d * u * (1 - s2*s1) / (Kb(p) + h) + n2d * v * (1 - s2/s1) / (Kb(p) - h);
a2d = -n1d * v * (1 - s2*s1) / (Kb(p) + h) - n2d * u * (1 - s2/s1) / (Kb(p) - h);
% iupwd0 - Diffuse flux scattered upward (reflected) above canopy (W/m2)
% iupwd - Diffuse flux scattered upward at the canopy depth (W/m2)
% idwnd - Diffuse flux scattered downward below canopy (W/m2)
% iabsd - Diffuse flux absorbed by canopy (W/m2)
% iabsd_sun - Diffuse flux absorbed by sunlit canopy (W/m2)
% iabsd_sha - Diffuse flux absorbed by shaded canopy (W/m2)
iupwd0 = n1d * u + n2d * v;
iupwd = n1d * u * s1 + n2d * v / s1;
idwnd = -n1d * v * s1 - n2d * u / s1;
iabsd = atmos.swskyd(p,ib) - iupwd0 + iupwd - idwnd;
iabsd_sun = (1 - omega(p,ib)) / avmu(p) * (a1d + a2d) * canopy.clumpfac(p);
iabsd_sha = iabsd - iabsd_sun;
% --- Save necessary radiative fluxes
% Albedo
suminc = atmos.swskyb(p,ib) + atmos.swskyd(p,ib);
sumref = iupwb0 + iupwd0;
if (suminc > 0)
flux.albcan(p,ib) = sumref / suminc;
else
flux.albcan(p,ib) = 0;
end
% Solar radiation absorbed by canopy
flux.swveg(p,ib) = iabsb + iabsd;
flux.swvegsun(p,ib) = iabsb_sun + iabsd_sun;
flux.swvegsha(p,ib) = iabsb_sha + iabsd_sha;
% Solar radiation absorbed by ground (soil)
dir = atmos.swskyb(p,ib) * s2 * (1 - flux.albsoib(p,ib));
dif = (idwnb + idwnd) * (1 - flux.albsoid(p,ib));
flux.swsoi(p,ib) = dir + dif;
% --- Conservation check: total incident = total reflected + total absorbed
suminc = atmos.swskyb(p,ib) + atmos.swskyd(p,ib);
sumref = iupwb0 + iupwd0;
sumabs = flux.swveg(p,ib) + flux.swsoi(p,ib);
err = suminc - (sumabs + sumref);
if (abs(err) > 1e-06)
fprintf('suminc = %15.5f\n',suminc)
fprintf('sumref = %15.5f\n',sumref)
fprintf('sumabs = %15.5f\n',sumabs)
error ('TwoStreamRadiation: Total solar radiation conservation error')
end
% --- Repeat two-stream calculations for each leaf layer to calculate leaf fluxes
icsun(ib) = 0;
icsha(ib) = 0;
for iv = canopy.nbot(p):canopy.ntop(p)
% s1 and s2 depend on cumulative lai
s1 = exp(-h * canopy.sumlai(p,iv) * canopy.clumpfac(p));
s2 = exp(-Kb(p) * canopy.sumlai(p,iv) * canopy.clumpfac(p));
% ilbb - absorbed direct beam flux (unscattered direct component) per unit leaf area
% at cumulative LAI, average for all leaves (J / m2 leaf / s)
ilbb = (1 - omega(p,ib)) * Kb(p) * atmos.swskyb(p,ib) * s2;
% ilbs - absorbed direct beam flux (scattered direct component) per unit leaf area
% at cumulative LAI, average for all leaves (J / m2 leaf / s)
diupwb = Kb(p) * g1 * s2 - h * n1b * u * s1 + h * n2b * v / s1;
didwnb = -Kb(p) * g2 * s2 + h * n1b * v * s1 - h * n2b * u / s1;
ilbs = (omega(p,ib) * Kb(p) * atmos.swskyb(p,ib) * s2 + (diupwb - didwnb)) * canopy.clumpfac(p);
% ild - absorbed diffuse flux per unit leaf area at cumulative LAI,
% average for all leaves (J / m2 leaf / s)
diupwd = -h * n1d * u * s1 + h * n2d * v / s1;
didwnd = h * n1d * v * s1 - h * n2d * u / s1;
ild = (diupwd - didwnd) * canopy.clumpfac(p);
% Save leaf fluxes per unit sunlit and shaded leaf area (W/m2 leaf)
flux.swleaf(p,iv,params.sun,ib) = ilbb / flux.fracsun(p,iv) + (ilbs + ild);
flux.swleaf(p,iv,params.sha,ib) = ilbs + ild;
icsun(ib) = icsun(ib) + (ilbb + (ilbs + ild)*flux.fracsun(p,iv)) * canopy.dlai(p,iv);
icsha(ib) = icsha(ib) + (ilbs + ild)*flux.fracsha(p,iv) * canopy.dlai(p,iv);
end % end canopy loop
end % end grid point loop
end % end waveband loop
% --- Adjust leaf fluxes as needed. The sum of the fluxes for sunlit and shaded
% leaves should equal the total absorbed by the canopy, but may not because of
% inaccuracies in the flux derivatives (this is a small error if the dlai increment
% is small). Normalize these fluxes to sum to the canopy absorption.
for ib = 1:params.numrad
for p = 1:params.npts
% Sum canopy absorption (W/m2 ground) using leaf fluxes per unit sunlit
% and shaded leaf area (W/m2 leaf)
sumabs = 0;
sumabs_sun = 0;
sumabs_sha = 0;
for iv = canopy.nbot(p):canopy.ntop(p)
sun = flux.swleaf(p,iv,params.sun,ib) * flux.fracsun(p,iv) * canopy.dlai(p,iv);
sha = flux.swleaf(p,iv,params.sha,ib) * flux.fracsha(p,iv) * canopy.dlai(p,iv);
sumabs = sumabs + sun + sha;
sumabs_sun = sumabs_sun + sun;
sumabs_sha = sumabs_sha + sha;
end
% Normalize profile
if (sumabs > 0)
for iv = canopy.nbot(p):canopy.ntop(p)
flux.swleaf(p,iv,params.sun,ib) = flux.swleaf(p,iv,params.sun,ib) * flux.swveg(p,ib) / sumabs;
flux.swleaf(p,iv,params.sha,ib) = flux.swleaf(p,iv,params.sha,ib) * flux.swveg(p,ib) / sumabs;
end
end
end
end
Output
Figures
Figure 1
Text
data.txt | View on GitHub | View raw
layer lai sun sha sun sha
1 0.0500 0.571710 0.179057 0.264662 0.126079
2 0.1500 0.559613 0.166960 0.264655 0.126072
3 0.2500 0.548363 0.155710 0.264276 0.125692
4 0.3500 0.537898 0.145246 0.263565 0.124982
5 0.4500 0.528163 0.135510 0.262560 0.123977
6 0.5500 0.519105 0.126452 0.261294 0.122711
7 0.6500 0.510674 0.118021 0.259800 0.121216
8 0.7500 0.502826 0.110173 0.258104 0.119520
9 0.8500 0.495519 0.102866 0.256233 0.117650
10 0.9500 0.488715 0.096062 0.254212 0.115628
11 1.0500 0.482378 0.089725 0.252061 0.113477
12 1.1500 0.476474 0.083821 0.249800 0.111217
13 1.2500 0.470973 0.078321 0.247449 0.108865
14 1.3500 0.465847 0.073195 0.245022 0.106439
15 1.4500 0.461069 0.068417 0.242535 0.103952
16 1.5500 0.456615 0.063962 0.240002 0.101418
17 1.6500 0.452462 0.059809 0.237434 0.098850
18 1.7500 0.448589 0.055936 0.234842 0.096259
19 1.8500 0.444976 0.052324 0.232237 0.093654
20 1.9500 0.441606 0.048953 0.229628 0.091044
21 2.0500 0.438462 0.045809 0.227021 0.088438
22 2.1500 0.435527 0.042874 0.224425 0.085841
23 2.2500 0.432788 0.040135 0.221845 0.083262
24 2.3500 0.430232 0.037579 0.219287 0.080704
25 2.4500 0.427845 0.035192 0.216756 0.078173
26 2.5500 0.425616 0.032963 0.214257 0.075674
27 2.6500 0.423535 0.030882 0.211793 0.073209
28 2.7500 0.421591 0.028938 0.209366 0.070783
29 2.8500 0.419775 0.027122 0.206981 0.068397
30 2.9500 0.418079 0.025426 0.204639 0.066055
31 3.0500 0.416495 0.023842 0.202341 0.063758
32 3.1500 0.415015 0.022362 0.200091 0.061508
33 3.2500 0.413632 0.020979 0.197888 0.059305
34 3.3500 0.412340 0.019687 0.195735 0.057151
35 3.4500 0.411133 0.018480 0.193630 0.055047
36 3.5500 0.410005 0.017352 0.191576 0.052993
37 3.6500 0.408952 0.016299 0.189572 0.050989
38 3.7500 0.407968 0.015316 0.187618 0.049034
39 3.8500 0.407050 0.014397 0.185713 0.047130
40 3.9500 0.406193 0.013540 0.183859 0.045275
41 4.0500 0.405393 0.012740 0.182053 0.043470
42 4.1500 0.404646 0.011994 0.180296 0.041713
43 4.2500 0.403950 0.011298 0.178586 0.040003
44 4.3500 0.403302 0.010649 0.176924 0.038341
45 4.4500 0.402699 0.010046 0.175307 0.036724
46 4.5500 0.402137 0.009485 0.173735 0.035152
47 4.6500 0.401616 0.008963 0.172207 0.033624
48 4.7500 0.401132 0.008480 0.170722 0.032139
49 4.8500 0.400684 0.008032 0.169278 0.030695
50 4.9500 0.400270 0.007617 0.167874 0.029291
51 5.0500 0.399888 0.007236 0.166509 0.027926
52 5.1500 0.399537 0.006885 0.165181 0.026598
53 5.2500 0.399216 0.006563 0.163890 0.025306
54 5.3500 0.398922 0.006270 0.162632 0.024049
55 5.4500 0.398656 0.006004 0.161408 0.022825
56 5.5500 0.398417 0.005764 0.160216 0.021633
57 5.6500 0.398203 0.005550 0.159054 0.020470
58 5.7500 0.398014 0.005361 0.157920 0.019336
59 5.8500 0.397849 0.005196 0.156813 0.018230
60 5.9500 0.397708 0.005056 0.155731 0.017148